2 5 As A Percentage
saludintensiva
Sep 11, 2025 · 5 min read
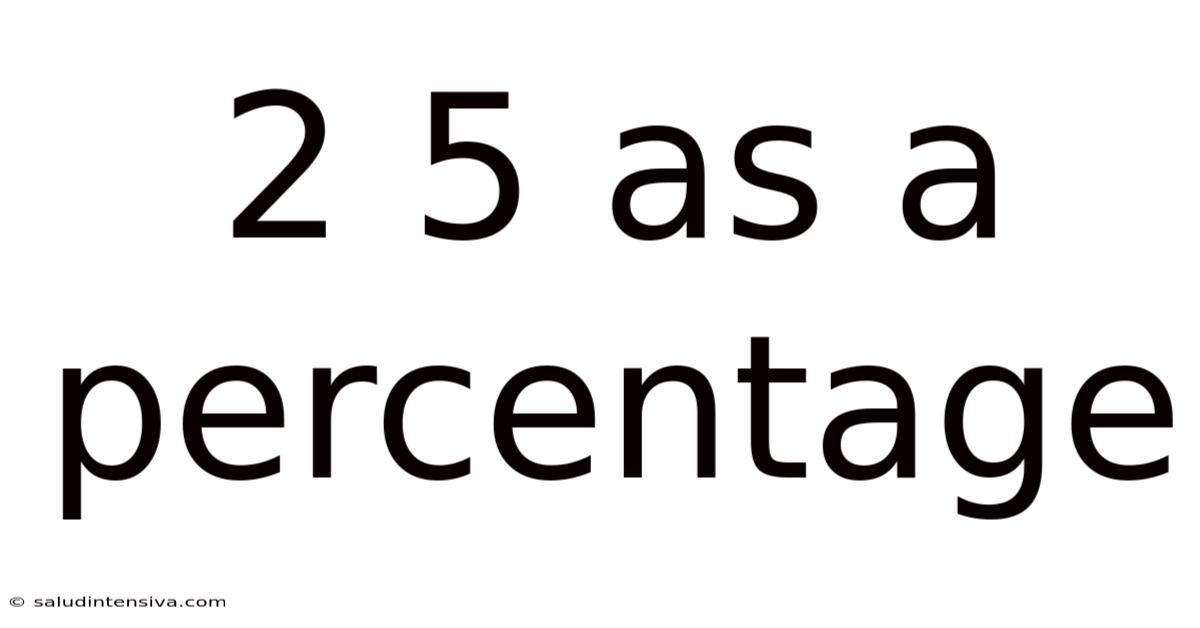
Table of Contents
Understanding 2/5 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics. This article will delve into the conversion of the fraction 2/5 into a percentage, providing a detailed explanation, various methods for solving it, and exploring its applications in real-world scenarios. We'll also address frequently asked questions and provide practical examples to solidify your understanding. This comprehensive guide will ensure you can confidently convert fractions to percentages and apply this knowledge effectively.
Introduction: What is a Percentage?
Before diving into the conversion of 2/5, let's establish a clear understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion or proportion out of a whole, where the whole is always considered to be 100%. This system is widely used in various fields, including finance, statistics, and everyday life. For instance, understanding percentages is crucial for calculating discounts, taxes, interest rates, and many other things.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is perhaps the most straightforward method. We'll first convert the fraction 2/5 into a decimal, and then convert the decimal to a percentage.
Step 1: Divide the numerator by the denominator.
To convert the fraction 2/5 to a decimal, we simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Step 2: Multiply the decimal by 100%.
To express the decimal as a percentage, we multiply it by 100%:
0.4 x 100% = 40%
Therefore, 2/5 is equal to 40%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the definition of percentage as "parts per hundred." We aim to find an equivalent fraction of 2/5 that has a denominator of 100.
Step 1: Determine the multiplier.
To change the denominator from 5 to 100, we need to multiply it by 20 (100 ÷ 5 = 20).
Step 2: Apply the multiplier to both the numerator and denominator.
To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same factor:
(2 x 20) / (5 x 20) = 40/100
Step 3: Express the fraction as a percentage.
Since the denominator is now 100, the numerator directly represents the percentage:
40/100 = 40%
Again, we find that 2/5 is equal to 40%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where the fraction 2/5 is equivalent to x/100, where 'x' represents the percentage we are looking for.
Step 1: Set up the proportion.
2/5 = x/100
Step 2: Cross-multiply.
To solve for 'x', we cross-multiply:
5x = 200
Step 3: Solve for x.
Divide both sides by 5:
x = 40
Therefore, x = 40%, confirming that 2/5 is equal to 40%.
The Scientific Explanation: Ratio and Proportion
The conversion of fractions to percentages relies on the fundamental mathematical concepts of ratio and proportion. A ratio is a comparison of two quantities, while a proportion is a statement of equality between two ratios. In our case, the ratio 2:5 is compared to the ratio x:100, where x represents the percentage. The solution involves finding the value of x that maintains the equality of these two ratios. This is achieved through cross-multiplication and solving for the unknown variable.
Real-world Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages has numerous practical applications in everyday life:
- Calculating discounts: If a store offers a 2/5 discount, you can quickly calculate this as a 40% discount.
- Understanding statistics: Many statistical representations use percentages to show proportions and trends. Converting fractions to percentages allows for easier interpretation of data.
- Financial calculations: Percentages are essential in calculating interest rates, taxes, profits, and losses.
- Grade calculations: In some grading systems, fractional scores are converted into percentages to represent a student's performance.
- Recipe adjustments: If a recipe calls for a fraction of an ingredient and you need to adjust the recipe size, converting the fraction to a percentage can simplify the calculations.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to percentages?
A: Yes, all fractions can be converted to percentages. This is because percentages are simply fractions with a denominator of 100. Even fractions with repeating decimals can be expressed as percentages, although the percentage might also have a repeating decimal.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: Improper fractions can also be converted to percentages. First, convert the improper fraction to a mixed number, then convert the fractional part to a decimal and then to a percentage. Finally, add the whole number part. For example, if you have 7/5, first convert it to 1 2/5 which can be converted to 1.4 and then to 140%.
Q: Are there any limitations to using percentages?
A: While percentages are widely used and incredibly useful, they can sometimes be misleading if not used carefully. It’s important to always consider the context and the original data when interpreting percentages. For instance, a small percentage increase on a large number can represent a substantial absolute change, and a large percentage decrease on a small number might not represent a significant absolute change.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting fractions like 2/5 into percentages is a crucial skill with far-reaching applications in various aspects of life. Understanding the different methods – whether it's converting to a decimal first, finding an equivalent fraction with a denominator of 100, or using proportions – provides flexibility and allows you to choose the approach that best suits your understanding and the problem at hand. By mastering this fundamental mathematical skill, you'll improve your ability to analyze data, solve problems efficiently, and interpret information more effectively in various real-world scenarios. Remember, practice is key to mastering this skill, so try converting different fractions into percentages to solidify your understanding. Remember, understanding the underlying principles of ratios and proportions makes this conversion process logical and easy to grasp.
Latest Posts
Latest Posts
-
55 Degrees Celsius To Kelvin
Sep 11, 2025
-
4 To The 2 Power
Sep 11, 2025
-
12 16 In Simplest Form
Sep 11, 2025
-
Greatest Common Factor For 48
Sep 11, 2025
-
Lcm Of 15 And 10
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 2 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.