2 6 In Simplest Form
saludintensiva
Sep 22, 2025 · 6 min read
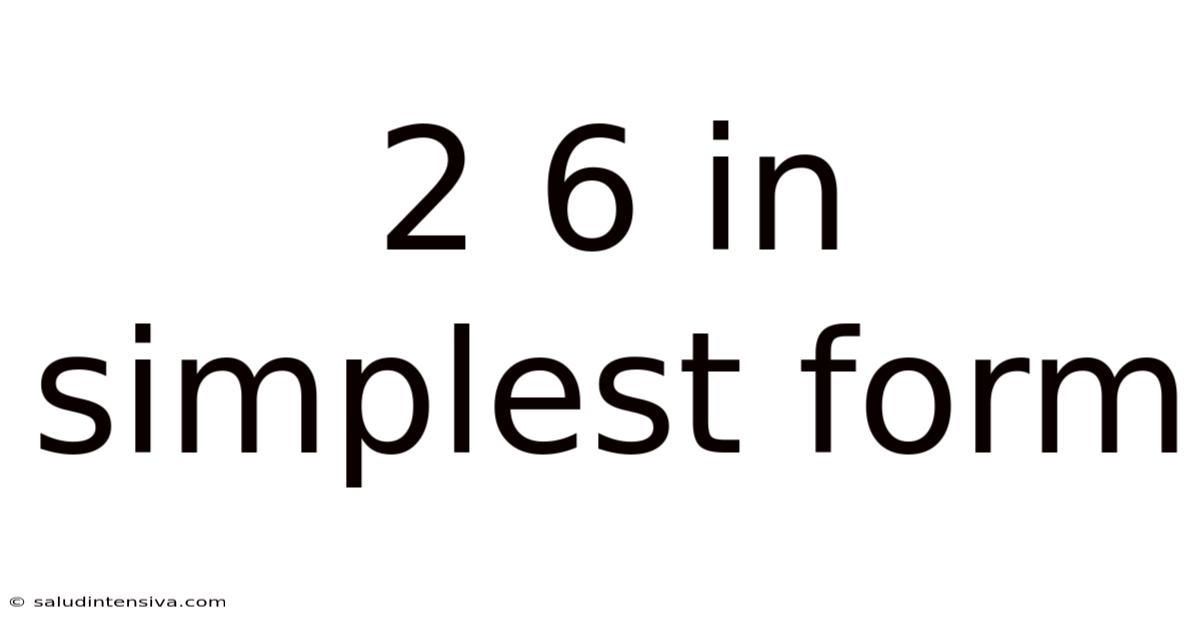
Table of Contents
Understanding Fractions: Simplifying 2/6 to its Simplest Form
Fractions are a fundamental concept in mathematics, representing parts of a whole. Learning to manipulate and simplify fractions is crucial for success in numerous mathematical fields, from basic arithmetic to advanced calculus. This article will delve into the process of simplifying fractions, using the example of 2/6, and explain the underlying mathematical principles. We'll explore why simplifying is important, and how to apply this skill to various fraction problems. Understanding how to simplify fractions like 2/6 will build a solid foundation for more complex mathematical concepts.
What is a Fraction?
A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/6, the numerator is 2 and the denominator is 6. This means we have 2 parts out of a total of 6 equal parts.
Simplifying Fractions: The Concept of Equivalent Fractions
Simplifying a fraction means reducing it to its simplest form while maintaining its value. This involves finding an equivalent fraction where the numerator and denominator have no common factors other than 1. Equivalent fractions represent the same proportion or value, just expressed differently. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions; they all represent one-half.
The key to simplifying is to find the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Simplifying 2/6: A Step-by-Step Guide
Let's simplify the fraction 2/6.
Step 1: Find the Greatest Common Divisor (GCD)
We need to find the largest number that divides both 2 and 6 without leaving a remainder. The factors of 2 are 1 and 2. The factors of 6 are 1, 2, 3, and 6. The largest number that appears in both lists is 2. Therefore, the GCD of 2 and 6 is 2.
Step 2: Divide Both the Numerator and Denominator by the GCD
Now, we divide both the numerator (2) and the denominator (6) by the GCD (2):
- 2 ÷ 2 = 1
- 6 ÷ 2 = 3
Step 3: Express the Simplified Fraction
The simplified fraction is 1/3. This means that 2/6 and 1/3 represent the same value; they are equivalent fractions. 1/3 is the simplest form because 1 and 3 share no common factors other than 1.
Visual Representation of 2/6 and 1/3
Imagine a pizza cut into 6 equal slices. 2/6 represents having 2 of those 6 slices. Now, imagine the same pizza cut into 3 equal slices. 1/3 represents having 1 of those 3 larger slices. You have the same amount of pizza in both scenarios, demonstrating the equivalence of 2/6 and 1/3.
Why is Simplifying Fractions Important?
Simplifying fractions is essential for several reasons:
- Clarity and Understanding: Simplified fractions are easier to understand and interpret. 1/3 is much clearer than 2/6.
- Easier Calculations: Simplifying fractions before performing other operations (addition, subtraction, multiplication, division) makes calculations significantly simpler and reduces the risk of errors.
- Standardized Representation: Simplifying fractions ensures a standardized and consistent representation of values. This is vital for communication and collaboration in mathematics.
- Problem-Solving: Many mathematical problems require fractions to be in their simplest form before proceeding to the solution.
Methods for Finding the Greatest Common Divisor (GCD)
While the factor method works well for smaller numbers, more efficient methods exist for larger numbers:
-
Prime Factorization: This method involves breaking down both the numerator and the denominator into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
For example, let's find the GCD of 12 and 18:
- 12 = 2² x 3
- 18 = 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
-
Euclidean Algorithm: This is a more efficient algorithm for finding the GCD of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 48 and 18 using the Euclidean Algorithm:
- 48 ÷ 18 = 2 with a remainder of 12
- 18 ÷ 12 = 1 with a remainder of 6
- 12 ÷ 6 = 2 with a remainder of 0
The last non-zero remainder is 6, so the GCD of 48 and 18 is 6.
Simplifying Fractions with Larger Numbers
Let's apply these methods to a more complex example: Simplify 24/36.
Using Prime Factorization:
- 24 = 2³ x 3
- 36 = 2² x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2², and the lowest power of 3 is 3¹. Therefore, the GCD is 2² x 3 = 12.
Dividing both the numerator and denominator by 12:
- 24 ÷ 12 = 2
- 36 ÷ 12 = 3
The simplified fraction is 2/3.
Using the Euclidean Algorithm:
- 36 ÷ 24 = 1 with a remainder of 12
- 24 ÷ 12 = 2 with a remainder of 0
The GCD is 12. Dividing both numerator and denominator by 12 results in 2/3.
Improper Fractions and Mixed Numbers
Sometimes, we encounter improper fractions, where the numerator is larger than or equal to the denominator (e.g., 7/4). These can be converted to mixed numbers, which combine a whole number and a proper fraction (e.g., 1 ¾). Simplifying is still important even with improper fractions; we simplify the fractional part of the mixed number.
For instance, let's simplify 10/6:
- Find the GCD of 10 and 6, which is 2.
- Divide both numerator and denominator by 2: 10/2 = 5 and 6/2 = 3.
- The simplified improper fraction is 5/3.
- To convert it to a mixed number, divide 5 by 3: 5 ÷ 3 = 1 with a remainder of 2.
- The mixed number is 1 ⅔.
Frequently Asked Questions (FAQ)
Q: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
A: Yes, you can, but it’s more efficient to divide by the greatest common factor. Dividing by smaller common factors might require multiple steps to reach the simplest form.
Q: What if the numerator and denominator have no common factors other than 1?
A: The fraction is already in its simplest form.
Q: Is there a way to check if a fraction is simplified?
A: Yes, check if the numerator and denominator have a GCD of 1. If they do, the fraction is simplified.
Q: Are there any online tools to simplify fractions?
A: Yes, many online calculators and websites are available to simplify fractions. However, understanding the manual process is crucial for building a strong mathematical foundation.
Conclusion
Simplifying fractions is a fundamental skill in mathematics. Understanding the concept of equivalent fractions and finding the greatest common divisor are crucial steps in this process. Whether using prime factorization or the Euclidean algorithm, the goal remains consistent: to represent the fraction in its clearest and most efficient form, enhancing mathematical understanding and simplifying calculations. The ability to simplify fractions like 2/6 to its simplest form, 1/3, provides a solid base for tackling more advanced mathematical concepts. Mastering this skill will undoubtedly contribute to greater success in future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 3 15 Simplified
Sep 22, 2025
-
80 Deg F To C
Sep 22, 2025
-
Demolition Of Concrete Slab Cost
Sep 22, 2025
-
19 Degrees Fahrenheit To Celsius
Sep 22, 2025
-
Multiplying Decimals Using Area Models
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 6 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.