2 8 In Lowest Terms
saludintensiva
Sep 18, 2025 · 5 min read
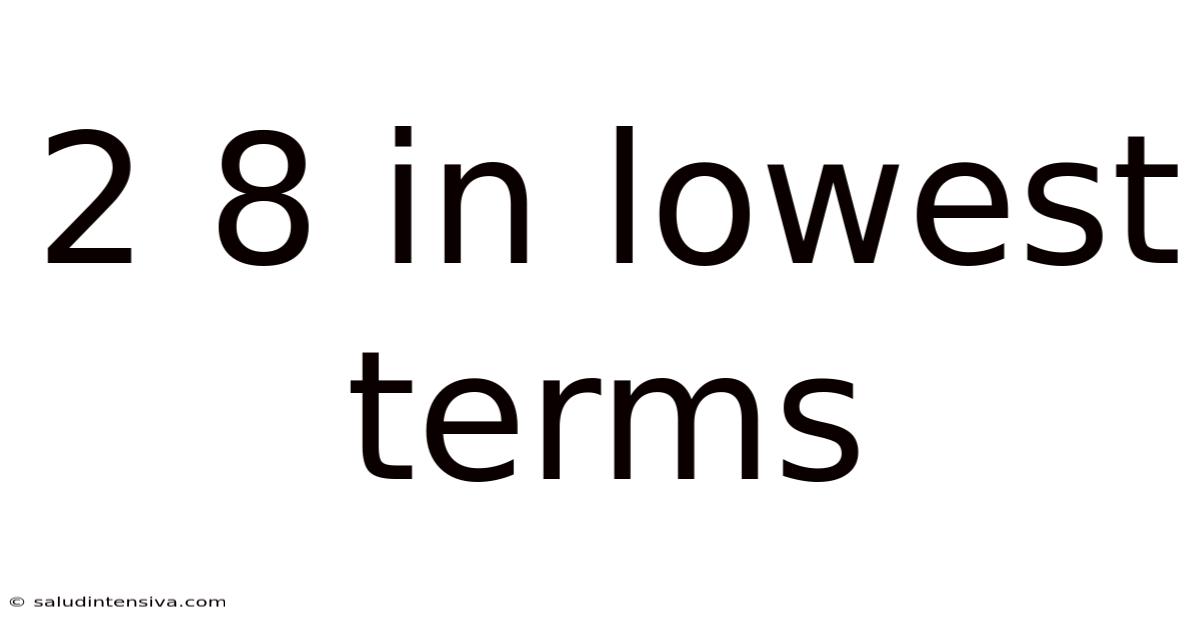
Table of Contents
Simplifying Fractions: Understanding 2/8 in Lowest Terms
Fractions are a fundamental concept in mathematics, representing parts of a whole. Learning to simplify, or reduce, fractions to their lowest terms is crucial for understanding mathematical relationships and solving various problems. This article will delve deep into the simplification of the fraction 2/8, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. We'll also uncover the broader implications of this seemingly simple concept and its relevance in various fields.
Introduction: What Does "Lowest Terms" Mean?
When we talk about a fraction being in its "lowest terms," or "simplest form," we mean that the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In simpler words, we can't divide both the top and bottom numbers by any whole number greater than 1 to get smaller whole numbers. This process of reducing a fraction to its lowest terms is called simplification.
Step-by-Step Simplification of 2/8
Let's break down how to simplify the fraction 2/8:
-
Find the Greatest Common Factor (GCF): The first step in simplifying any fraction is to identify the greatest common factor (GCF) of the numerator and the denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder. For 2 and 8, the factors are:
- Factors of 2: 1, 2
- Factors of 8: 1, 2, 4, 8
The greatest number that appears in both lists is 2. Therefore, the GCF of 2 and 8 is 2.
-
Divide Both Numerator and Denominator by the GCF: Once we've found the GCF, we divide both the numerator and the denominator by this number.
- 2 ÷ 2 = 1
- 8 ÷ 2 = 4
-
The Simplified Fraction: The result of this division gives us the simplified fraction: 1/4. This means that 2/8 and 1/4 represent the same value; they are equivalent fractions. Since 1 and 4 share no common factors other than 1, 1/4 is the simplest form of 2/8.
Mathematical Explanation: Prime Factorization and Equivalent Fractions
The process of simplifying fractions is rooted in the concept of equivalent fractions. Equivalent fractions represent the same value but are expressed with different numerators and denominators. To understand this better, let's use prime factorization.
Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
Now, let's rewrite the fraction 2/8 using the prime factorizations:
2/8 = (2) / (2 x 2 x 2)
Notice that we have a common factor of 2 in both the numerator and the denominator. We can cancel out this common factor:
(2) / (2 x 2 x 2) = 1 / (2 x 2) = 1/4
This method clearly shows how simplifying a fraction involves canceling out common factors to arrive at the simplest form.
Visual Representation: Understanding Fractions with Diagrams
Visualizing fractions can significantly improve understanding. Let's represent 2/8 using a diagram:
Imagine a pizza cut into 8 equal slices. The fraction 2/8 represents 2 out of those 8 slices. If we group the slices, we can see that these 2 slices represent 1 out of 4 equal parts of the pizza. This visually demonstrates the equivalence of 2/8 and 1/4.
Applications of Fraction Simplification in Real-World Scenarios
Simplifying fractions isn't just an abstract mathematical exercise; it has practical applications in various real-world situations:
-
Cooking and Baking: Recipes often involve fractions. Simplifying fractions helps in accurately measuring ingredients. For example, if a recipe calls for 2/8 cup of sugar, you'd know it's the same as 1/4 cup.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Simplifying fractions allows for efficient and accurate calculations.
-
Finance and Accounting: Working with budgets and financial statements often involves fractions. Simplifying fractions makes it easier to understand and interpret financial data.
-
Data Analysis and Statistics: Fractions are frequently used in data analysis and statistics. Simplifying fractions makes the data easier to understand and interpret.
Beyond 2/8: General Strategies for Simplifying Fractions
The process of simplifying 2/8 can be generalized to simplify any fraction:
-
Find the GCF: Determine the greatest common factor of the numerator and the denominator. You can use prime factorization or list the factors to find the GCF.
-
Divide: Divide both the numerator and the denominator by the GCF.
-
Check: Ensure that the resulting fraction has no common factors other than 1.
Frequently Asked Questions (FAQ)
-
Q: What if the numerator is larger than the denominator?
- A: If the numerator is larger than the denominator, you have an improper fraction. You can simplify it in the same way as a proper fraction, and then convert it to a mixed number (a whole number and a fraction).
-
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
- A: No, you must divide both the numerator and the denominator by the same number to maintain the fraction's value. Dividing by different numbers would change the value of the fraction.
-
Q: What if the GCF is 1?
- A: If the GCF is 1, the fraction is already in its simplest form. It cannot be simplified further.
-
Q: Are there any shortcuts for finding the GCF?
- A: For smaller numbers, listing factors is often sufficient. For larger numbers, the Euclidean algorithm is a more efficient method for finding the GCF.
Conclusion: Mastering Fraction Simplification
Simplifying fractions like 2/8 to its simplest form, 1/4, is a fundamental skill in mathematics. Understanding the underlying principles of greatest common factors, equivalent fractions, and prime factorization is crucial for mastering this skill. This seemingly simple process has far-reaching applications in various fields, making it an essential part of mathematical literacy. By understanding the step-by-step process and practicing regularly, you'll build a strong foundation in fractions and unlock a deeper understanding of mathematical concepts. Remember, practice is key to mastering this valuable skill! Through consistent practice and a grasp of the underlying principles, you can confidently simplify fractions and apply this knowledge to solve various mathematical problems in your academic and professional life.
Latest Posts
Latest Posts
-
What Is This Number Pronounces
Sep 18, 2025
-
Greatest Common Factor Of 100
Sep 18, 2025
-
1 2 As An Improper Fraction
Sep 18, 2025
-
8 64 As A Fraction
Sep 18, 2025
-
2 To The Fourth Power
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 8 In Lowest Terms . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.