2 To Power Of 2
saludintensiva
Sep 25, 2025 · 6 min read
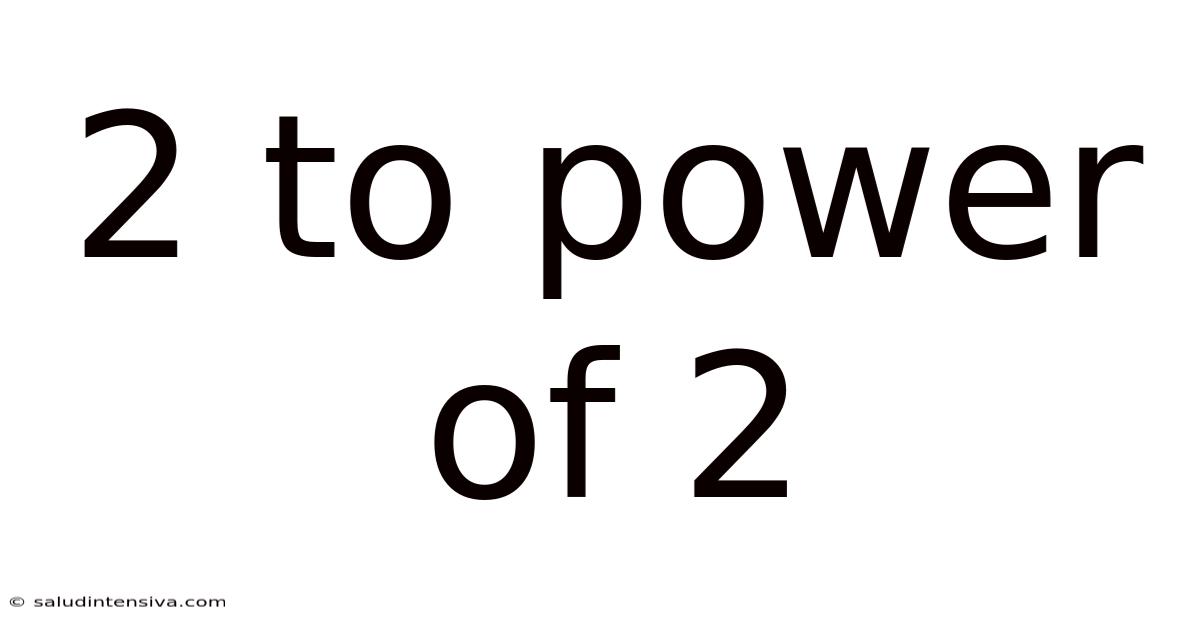
Table of Contents
Decoding 2 to the Power of 2: Exploring Exponentiation and its Applications
Introduction:
What exactly is 2 to the power of 2, and why should we care? This seemingly simple mathematical expression, often written as 2², unlocks a gateway to understanding fundamental concepts in mathematics, computer science, and even everyday life. This article will delve deep into the meaning of 2², explore its broader implications within exponentiation, and uncover its surprising applications in diverse fields. We will move beyond a simple calculation to grasp the underlying principles and significance of this seemingly basic mathematical concept.
Understanding Exponentiation: The Power of Powers
Before we dive into the specifics of 2², let's solidify our understanding of exponentiation. Exponentiation is a mathematical operation that involves raising a base number to a specific power (or exponent). It represents repeated multiplication of the base number by itself. In the general form, a<sup>b</sup>, 'a' is the base and 'b' is the exponent. This means we multiply 'a' by itself 'b' times.
For instance:
- 3² (3 to the power of 2) = 3 x 3 = 9
- 5³ (5 to the power of 3) = 5 x 5 x 5 = 125
- 2⁴ (2 to the power of 4) = 2 x 2 x 2 x 2 = 16
These examples demonstrate how the exponent dictates the number of times the base is multiplied. Now, let's focus on our subject: 2².
Calculating 2 to the Power of 2 (2²)
2² simply means 2 multiplied by itself twice: 2 x 2 = 4. Therefore, the answer to 2 to the power of 2 is 4. While seemingly trivial, this simple calculation forms the basis for understanding more complex exponential relationships and their applications.
Beyond the Calculation: The Significance of 2²
The significance of 2² extends far beyond its simple numerical value. Its importance stems from its role as a foundational element within several mathematical and computational concepts:
-
Binary System: The binary system, the foundation of modern computing, uses only two digits: 0 and 1. Understanding powers of 2 is crucial because each bit (binary digit) in a computer represents a power of 2. For example, an 8-bit number can represent 2⁸ (256) different values. The value of 2² directly relates to the representation of four distinct values (00, 01, 10, 11) within the binary system.
-
Geometric Progressions: 2² appears frequently in geometric progressions, where each term is obtained by multiplying the previous term by a constant value (in this case, 2). This pattern appears in various real-world scenarios, such as population growth (under ideal conditions) or compound interest calculations. Understanding the progression powered by 2² aids in predicting future values within these sequences.
-
Combinatorics and Probability: The calculation of combinations and permutations, critical in probability theory, often involves powers of 2. For example, if you have two choices for each of two decisions, the total number of possible outcomes is 2 x 2 = 2² = 4. This extends to more complex scenarios where the number of choices increases, leading to higher powers of 2.
-
Area Calculation: In geometry, 2² can represent the area of a square with sides of length 2 units. This simple geometric application highlights the connection between exponentiation and spatial dimensions.
Expanding the Scope: Higher Powers of 2
Understanding 2² allows us to extrapolate to higher powers of 2, which are essential in various fields:
-
2³ (8): Represents the number of corners in a cube or the number of bytes in a kilobyte (approximately, due to the use of powers of 2 in computer memory addressing).
-
2⁴ (16): Represents the number of bits in a 16-bit system or the number of elements in a 4x4 matrix.
-
2¹⁰ (1024): Approximately 1 kilobyte (KB) in computer memory. This illustrates how powers of 2 are integral to computer memory organization.
-
2²⁰ (1,048,576): Approximately 1 megabyte (MB). This demonstrates the exponential growth associated with powers of 2.
This pattern continues, demonstrating the immense impact of powers of 2 on data storage and processing capabilities in computer science.
Applications of 2² and Powers of 2 in Real-World Scenarios
The applications of 2² and its higher-order counterparts extend far beyond theoretical mathematics:
-
Computer Science: As already mentioned, powers of 2 form the backbone of computer memory, addressing, and data representation. Understanding these principles is crucial for software development and hardware design.
-
Finance: Compound interest calculations frequently utilize exponential functions, with powers of 2 appearing in scenarios involving doubling time or growth rates.
-
Biology: Bacterial growth under ideal conditions often follows an exponential pattern, with population doubling at regular intervals. This involves powers of 2 in modeling population dynamics.
-
Physics: Exponential decay and growth models appear in various physical phenomena, such as radioactive decay or the charging and discharging of capacitors.
Frequently Asked Questions (FAQ)
Q: What is the difference between 2² and 2 x 2?
A: There is no difference. 2² is simply a shorthand notation for 2 x 2, representing 2 multiplied by itself twice.
Q: Why are powers of 2 so important in computing?
A: The binary system, which underlies all digital computing, utilizes only two digits (0 and 1). Representing data and performing calculations in binary necessitate the use of powers of 2 for efficient memory management and data handling.
Q: Are there any other ways to represent 2² besides 2 x 2?
A: While 2 x 2 is the most straightforward representation, it can also be expressed as √16 (the square root of 16) or as 4. All these expressions represent the same value.
Q: Can negative exponents be used with 2?
A: Yes. A negative exponent indicates the reciprocal. For instance, 2⁻² = 1/2² = 1/4 = 0.25.
Q: How does 2² relate to other mathematical concepts?
A: 2² is connected to various mathematical ideas including geometric progressions, combinatorics, logarithms, and the study of exponential functions. Its simplicity masks a deep connection to broader mathematical principles.
Conclusion: The Unsung Hero of Mathematics and Computing
While 2 to the power of 2 might initially appear to be a trivial calculation, its significance reaches far beyond the simple answer of 4. Its impact on various fields, from computer science to finance and biology, is profound. By understanding the underlying principles of exponentiation and the specific role of 2², we unlock a deeper appreciation for the intricate workings of mathematics and its power to model and explain phenomena across multiple disciplines. Its seemingly simple nature belies its crucial role as a building block for a vast array of complex concepts and real-world applications. The journey from 2 x 2 to understanding the far-reaching implications of 2² underscores the beauty and utility of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Lcm Of 30 And 48
Sep 25, 2025
-
Convert 125 Pounds To Kilos
Sep 25, 2025
-
Whats 50 Cm In Inches
Sep 25, 2025
-
42000 Sq Ft To Acres
Sep 25, 2025
-
126 Sq Ft To M2
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 2 To Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.