20/3 As A Mixed Number
saludintensiva
Sep 12, 2025 · 5 min read
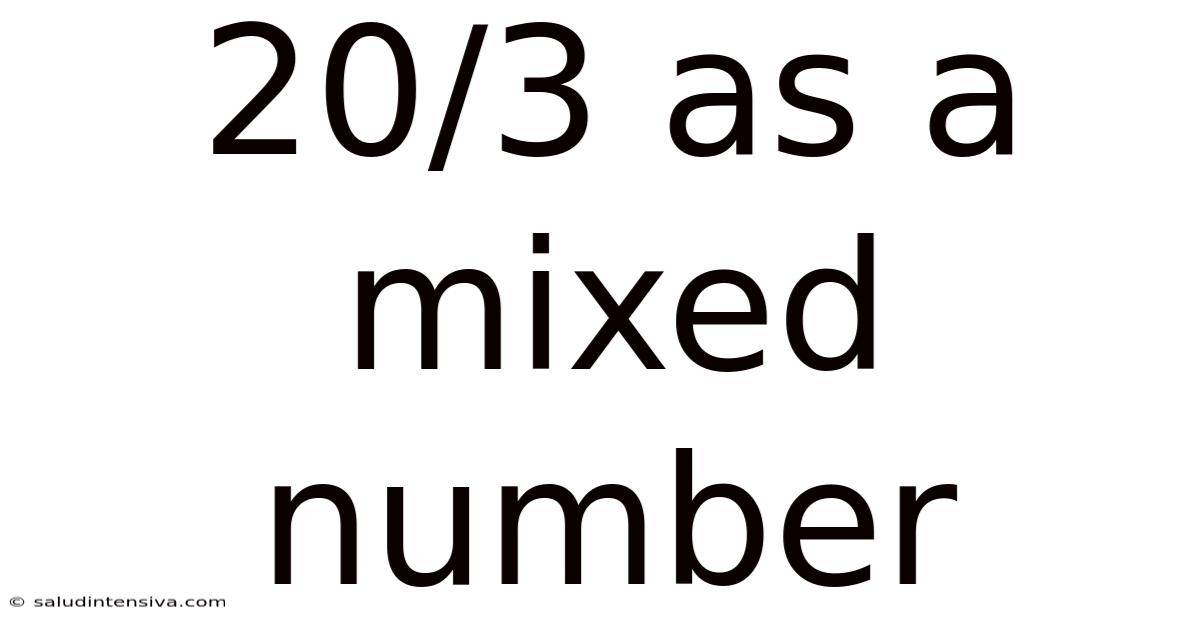
Table of Contents
Understanding 20/3 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 20/3 might appear straightforward at first glance. However, understanding it fully involves delving into the concept of mixed numbers, improper fractions, and the crucial relationship between them. This comprehensive guide will not only show you how to convert 20/3 into a mixed number but also equip you with a deeper understanding of the underlying mathematical principles. We'll explore various methods, address common misconceptions, and delve into the practical applications of this conversion. This will serve as a valuable resource for students learning fractions and anyone seeking a clearer grasp of this fundamental mathematical concept.
What are Mixed Numbers and Improper Fractions?
Before diving into the conversion of 20/3, let's clarify the terminology. A fraction represents a part of a whole. There are two main types of fractions:
-
Proper Fractions: These fractions have a numerator (the top number) that is smaller than the denominator (the bottom number). For example, 1/2, 3/4, and 5/8 are proper fractions. They represent a value less than one.
-
Improper Fractions: These fractions have a numerator that is greater than or equal to the denominator. Examples include 7/4, 11/5, and 20/3. They represent a value greater than or equal to one.
A mixed number combines a whole number and a proper fraction. For instance, 1 1/2, 2 3/4, and 5 1/8 are mixed numbers. They represent a value that's a combination of whole units and a fractional part.
The fraction 20/3 is an improper fraction because the numerator (20) is larger than the denominator (3). Converting it to a mixed number allows for a clearer representation of its value.
Converting 20/3 to a Mixed Number: Step-by-Step Guide
There are several ways to convert an improper fraction like 20/3 into a mixed number. Here's a step-by-step guide using the most common method:
Method 1: Division
-
Divide the numerator by the denominator: Divide 20 by 3. This gives you a quotient (the whole number part of the mixed number) and a remainder (the numerator of the fractional part).
20 ÷ 3 = 6 with a remainder of 2
-
The quotient becomes the whole number part: The quotient, 6, is the whole number part of your mixed number.
-
The remainder becomes the numerator of the fractional part: The remainder, 2, becomes the numerator of the fraction.
-
The denominator remains the same: The denominator of the fraction in the mixed number stays the same as the original fraction's denominator, which is 3.
Therefore, 20/3 as a mixed number is 6 2/3.
Method 2: Repeated Subtraction
This method is particularly helpful for visualizing the concept.
-
Subtract the denominator from the numerator repeatedly: Keep subtracting the denominator (3) from the numerator (20) until the result is less than the denominator.
20 - 3 = 17 17 - 3 = 14 14 - 3 = 11 11 - 3 = 8 8 - 3 = 5 5 - 3 = 2
-
Count the number of subtractions: You subtracted 3 from 20 six times before reaching a remainder less than 3. This number of subtractions (6) is the whole number part of your mixed number.
-
The final remainder is the numerator: The remaining 2 is the numerator of the fractional part.
-
The denominator remains unchanged: The denominator remains 3.
Again, this gives us the mixed number 6 2/3.
Visualizing the Conversion
Imagine you have 20 identical objects, and you want to group them into sets of 3. You can form 6 complete sets of 3, with 2 objects left over. This visually represents the 6 whole units (the 6 in the mixed number) and the remaining 2/3.
Why Convert to a Mixed Number?
Converting an improper fraction to a mixed number often offers a more intuitive and easily understandable representation of the value. While 20/3 is perfectly valid, 6 2/3 is often easier to grasp and use in practical contexts. For example, if you're measuring something, 6 2/3 inches is much clearer than 20/3 inches.
Addressing Common Misconceptions
A frequent misunderstanding is incorrectly adding the remainder to the denominator. Remember, the denominator represents the size of the fractional parts, and it should remain constant throughout the conversion process.
Further Applications and Extensions
The conversion of improper fractions to mixed numbers is fundamental to various mathematical operations, including:
-
Addition and subtraction of fractions: It's often easier to add or subtract mixed numbers than improper fractions.
-
Multiplication and division of fractions: While it's not always necessary, converting to mixed numbers can sometimes simplify these operations.
-
Problem-solving in real-world contexts: Many real-world situations involve fractional quantities, and converting to mixed numbers can make the solutions more understandable.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, any improper fraction can be converted to a mixed number.
Q: Is there only one way to represent a value as a mixed number?
A: No, the representation of a value as a mixed number can be simplified. For example, you might obtain a result like 6 6/6 which can be simplified further to 7.
Q: What if I get a remainder of 0 after division?
A: If the remainder is 0, it means the improper fraction is equivalent to a whole number. For example, 12/3 = 4.
Q: What if the fraction is negative?
A: Simply perform the conversion as described above and then add a negative sign to the resulting mixed number. For example, -20/3 = -6 2/3.
Conclusion
Converting an improper fraction like 20/3 into a mixed number is a fundamental skill in arithmetic. This process enhances our understanding of fractions and their real-world applications. Through various methods, including division and repeated subtraction, we can effectively transform improper fractions into a more accessible and intuitive mixed number representation. Understanding the underlying principles and practicing these methods will solidify your understanding of fractions and contribute to your overall mathematical proficiency. The ability to easily convert between improper fractions and mixed numbers is a crucial skill that will serve you well in many mathematical endeavors. Remember to practice regularly and don't hesitate to revisit these steps whenever needed. With consistent effort, mastering this concept will become second nature.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 80
Sep 12, 2025
-
3 5 Is Equal To What
Sep 12, 2025
-
Lcm Of 6 And 18
Sep 12, 2025
-
Sum Of The Years Depreciation
Sep 12, 2025
-
1 6 2 In Fraction
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 20/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.