21 Percent As A Decimal
saludintensiva
Sep 19, 2025 · 5 min read
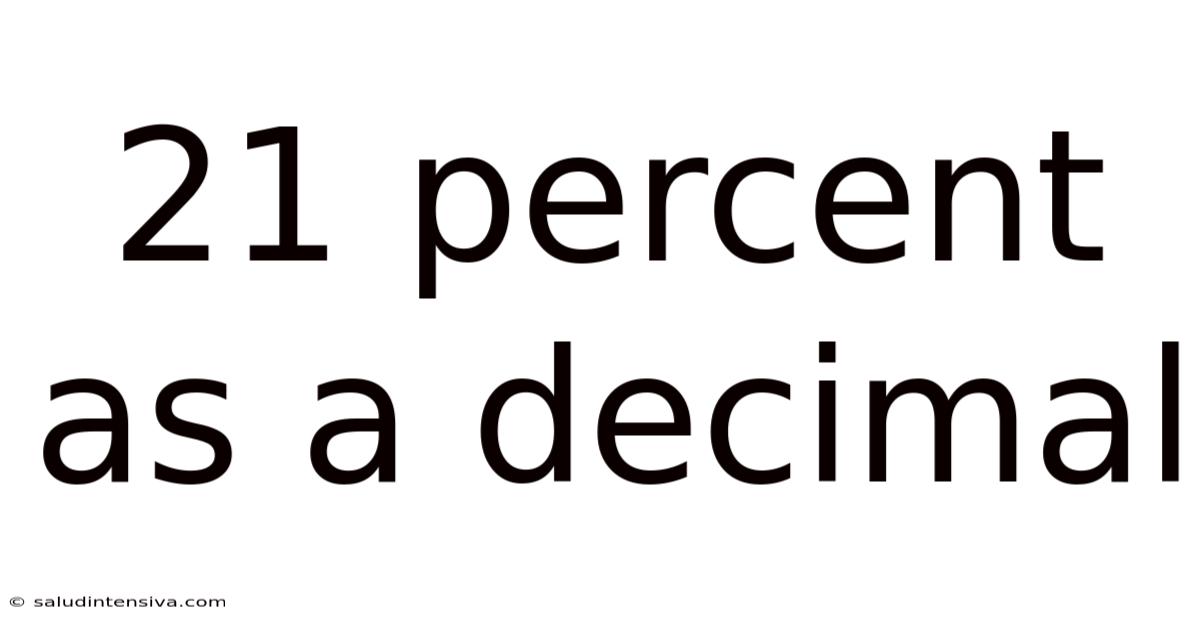
Table of Contents
21 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and crucial for various applications in everyday life, from calculating discounts to understanding financial reports. This article provides a comprehensive guide to converting 21 percent to its decimal form, explaining the process in detail and exploring related concepts to solidify your understanding. We'll cover the basic principles, delve into the practical implications, and answer frequently asked questions.
Introduction: The World of Percentages and Decimals
Percentages and decimals are two different ways of representing the same thing: a portion or fraction of a whole. A percentage expresses this portion as a fraction of 100, while a decimal represents it as a fraction of 1 (or a power of 10). Knowing how to convert between these two forms is vital for accurate calculations and clear communication of numerical data. This article focuses specifically on converting 21%, a common percentage encountered in various contexts, into its decimal equivalent. We'll break down the conversion process step-by-step and then explore some real-world applications to illustrate its relevance.
Understanding the Conversion Process: From Percentage to Decimal
The core concept behind converting a percentage to a decimal is understanding that the percent symbol (%) signifies "per hundred" or "out of 100." Therefore, 21% means 21 out of 100, which can be written as the fraction 21/100. To convert this fraction to a decimal, we simply divide the numerator (21) by the denominator (100):
21 ÷ 100 = 0.21
Therefore, 21% as a decimal is 0.21.
This conversion can be generalized. To convert any percentage to a decimal, follow these simple steps:
- Remove the percent sign (%): This leaves you with the numerical value of the percentage.
- Divide the number by 100: This is equivalent to moving the decimal point two places to the left.
Let's illustrate with a few more examples:
- 50% = 50 ÷ 100 = 0.50 or 0.5
- 10% = 10 ÷ 100 = 0.10 or 0.1
- 125% = 125 ÷ 100 = 1.25
- 0.5% = 0.5 ÷ 100 = 0.005
Practical Applications of 21% as a Decimal
The decimal equivalent of 21% (0.21) finds numerous applications in various fields. Here are a few examples:
-
Calculating Sales Tax: If the sales tax in your region is 21%, you can easily calculate the tax amount on an item by multiplying the item's price by 0.21. For example, a $100 item would have a tax of $100 * 0.21 = $21.
-
Determining Discounts: A 21% discount on an item can be calculated by multiplying the original price by 0.21 to find the discount amount, and then subtracting this amount from the original price to get the final price. For instance, a $50 item with a 21% discount would cost $50 - ($50 * 0.21) = $39.50.
-
Financial Calculations: In finance, percentages and decimals are frequently used to calculate interest rates, returns on investment, and other key financial metrics. A 21% interest rate, for example, would be represented as 0.21 in most financial formulas.
-
Statistical Analysis: Percentages and decimals are extensively used in statistical analysis to represent proportions, probabilities, and other important statistical measures. Converting 21% to 0.21 makes calculations within statistical models simpler and more efficient.
-
Scientific Applications: Many scientific fields, like chemistry and physics, require precise calculations involving percentages and proportions. Converting percentages to decimals ensures accuracy and facilitates easier computations.
Further Exploration: Working with Percentages and Decimals
Understanding the relationship between percentages and decimals is essential for a strong grasp of mathematics and its various applications. Here are some related concepts to further enhance your understanding:
-
Converting Decimals to Percentages: The reverse process of converting a decimal to a percentage involves multiplying the decimal by 100 and adding the percent sign (%). For example, 0.21 * 100 = 21%, confirming our earlier conversion.
-
Fractions, Decimals, and Percentages: These three concepts are interconnected. A fraction represents a part of a whole, a decimal expresses it in base-10 notation, and a percentage shows it as a fraction of 100. Converting between these forms is a vital skill in mathematical problem-solving.
-
Compound Interest: Understanding percentages and decimals is crucial for comprehending compound interest calculations. Compound interest involves earning interest on both the principal amount and accumulated interest.
-
Percentage Change: Calculating percentage change, often used to compare values over time, requires converting percentage differences into decimals to perform calculations.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to convert percentages to decimals?
- A: Converting percentages to decimals is essential for performing calculations using calculators, computers, and various mathematical formulas. Many equations and software programs require decimal input for accurate computations.
-
Q: Can I directly input 21% into a calculator for calculations?
- A: While some calculators have percentage functions, it's generally more reliable to convert the percentage to its decimal equivalent (0.21) before entering it into the calculation to ensure accuracy, particularly when dealing with complex equations.
-
Q: What if the percentage has a decimal point itself, such as 21.5%?
- A: You follow the same process: remove the percentage sign and divide by 100. In this case, 21.5% becomes 21.5 ÷ 100 = 0.215.
-
Q: Are there any situations where it's better to use percentages rather than decimals?
- A: Percentages are often preferred in presentations and communication to make numerical data easier to understand and interpret, as they provide a more intuitive representation of proportions. However, for most mathematical calculations, decimals are generally more efficient and accurate.
-
Q: How do I calculate 21% of a number using its decimal equivalent?
- A: To find 21% of any number, simply multiply that number by its decimal equivalent, 0.21. For example, 21% of 500 is 500 * 0.21 = 105.
Conclusion: Mastering the Conversion and Its Applications
Converting 21% to its decimal equivalent, 0.21, is a straightforward yet crucial mathematical skill. This seemingly simple conversion forms the foundation for numerous calculations in various fields, from daily financial transactions to complex scientific computations. By understanding the conversion process and exploring its diverse applications, you'll enhance your numerical literacy and improve your ability to solve practical problems effectively. Remember that a strong grasp of percentages and decimals is vital for navigating the numerical world with confidence and precision. This understanding will serve you well in many aspects of your life, both personally and professionally.
Latest Posts
Latest Posts
-
5 Divided By 1 1 4
Sep 19, 2025
-
All The Multiples Of 16
Sep 19, 2025
-
11 000 Minutes To Hours
Sep 19, 2025
-
3 To The Tenth Power
Sep 19, 2025
-
5000 Sq Ft To Acres
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 21 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.