25/18 As A Mixed Number
saludintensiva
Sep 23, 2025 · 5 min read
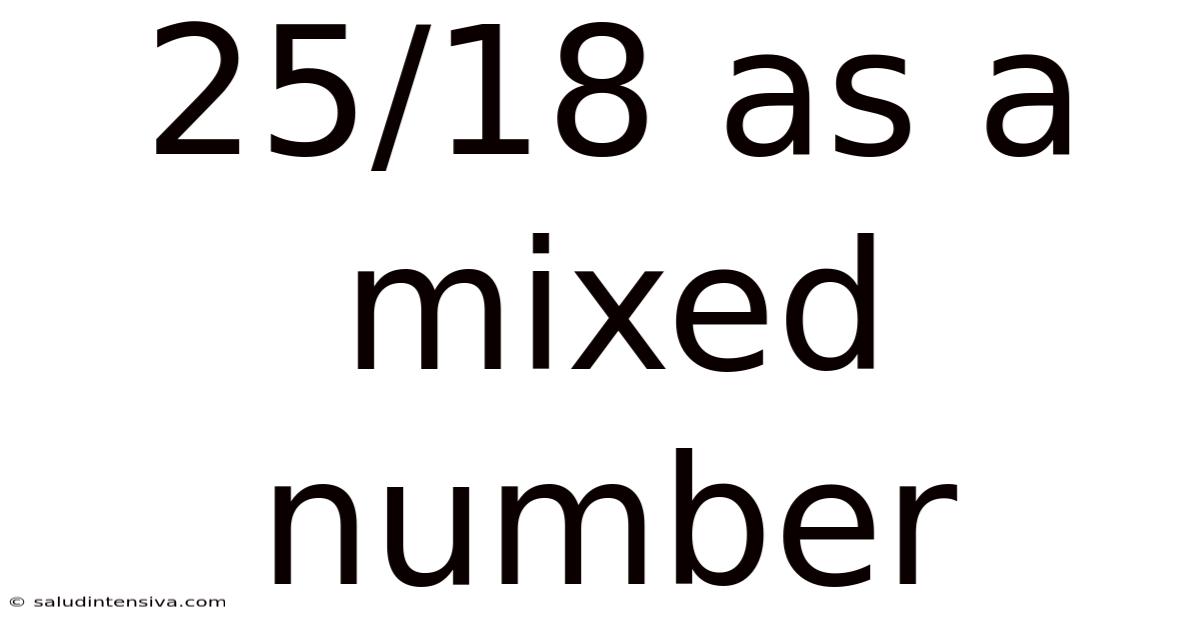
Table of Contents
Understanding 25/18 as a Mixed Number: A Comprehensive Guide
The concept of mixed numbers is fundamental in mathematics, bridging the gap between fractions and whole numbers. This article provides a comprehensive guide to understanding and converting improper fractions, like 25/18, into their mixed number equivalent. We'll explore the process step-by-step, delve into the underlying mathematical principles, and address frequently asked questions. This will equip you with a solid understanding of this essential mathematical concept.
Introduction: What are Mixed Numbers?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾ is a mixed number, representing one whole and three-quarters. In contrast, an improper fraction has a numerator that is greater than or equal to the denominator, such as 7/4 or 25/18. Understanding how to convert between improper fractions and mixed numbers is crucial for various mathematical operations and real-world applications.
Converting 25/18 to a Mixed Number: A Step-by-Step Guide
The conversion of an improper fraction to a mixed number involves division. Let's break down the process using the example of 25/18:
-
Divide the Numerator by the Denominator: This is the core of the conversion process. Divide 25 (the numerator) by 18 (the denominator).
25 ÷ 18 = 1 with a remainder of 7
-
Identify the Whole Number: The quotient (the result of the division) becomes the whole number part of your mixed number. In this case, the quotient is 1.
-
Identify the Remainder: The remainder from the division becomes the numerator of the fractional part of your mixed number. Here, the remainder is 7.
-
Keep the Original Denominator: The denominator of the fraction in your mixed number remains the same as the original denominator. So, the denominator stays as 18.
-
Combine the Whole Number and Fraction: Put the whole number and the fraction together to form your mixed number. Therefore, 25/18 as a mixed number is 1 ⁷⁄₁₈.
Visualizing the Conversion: A Practical Approach
Imagine you have 25 equally sized pieces of pizza. Each slice represents 1/18th of a whole pizza. To convert 25/18 to a mixed number, we group these slices into whole pizzas.
We can make one complete pizza (18 slices) using 18 of the 25 slices. We'll have 7 slices remaining. Therefore, we have 1 whole pizza and 7/18 of a pizza left, which visually represents the mixed number 1 ⁷⁄₁₈.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the fundamental principle of division and the concept of equivalent fractions. We can express the improper fraction 25/18 as:
25/18 = (18 + 7)/18
This can be rewritten using the addition property of fractions:
(18/18) + (7/18) = 1 + 7/18 = 1 ⁷⁄₁₈
This demonstrates that the process of converting an improper fraction to a mixed number is mathematically sound and consistent with the fundamental rules of fraction manipulation.
Beyond 25/18: Applying the Method to Other Improper Fractions
The method described above can be applied to any improper fraction. Let's consider a few more examples:
-
17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ²/₅
-
29/6: 29 ÷ 6 = 4 with a remainder of 5. Therefore, 29/6 = 4 ⁵⁄₆
-
31/10: 31 ÷ 10 = 3 with a remainder of 1. Therefore, 31/10 = 3 ¹⁄₁₀
By consistently following the steps of dividing the numerator by the denominator, identifying the whole number and the remainder, and combining them into a mixed number, you can easily convert any improper fraction into its mixed number equivalent.
Converting Mixed Numbers Back to Improper Fractions
The process is reversible. To convert a mixed number back to an improper fraction, follow these steps:
-
Multiply the whole number by the denominator: For example, in 1 ⁷⁄₁₈, multiply 1 (whole number) by 18 (denominator) = 18
-
Add the numerator: Add the result from step 1 to the numerator of the fraction (7). 18 + 7 = 25
-
Keep the same denominator: The denominator remains 18.
-
Form the improper fraction: The result is 25/18, the original improper fraction.
Frequently Asked Questions (FAQs)
Q1: What if the remainder is zero?
A1: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 18/18 = 1. There is no fractional part in the mixed number.
Q2: Can I convert any fraction into a mixed number?
A2: No, you can only convert improper fractions (where the numerator is greater than or equal to the denominator) into mixed numbers. Proper fractions (where the numerator is less than the denominator) already represent a portion of a whole and cannot be further converted into a mixed number.
Q3: Why is understanding mixed numbers important?
A3: Mixed numbers are essential for many practical applications and further mathematical studies. They provide a more intuitive way to represent quantities that are greater than one but not necessarily whole numbers. They are commonly used in measurements, cooking, and various problem-solving scenarios.
Q4: Are there other ways to represent 25/18?
A4: Yes, while 1 ⁷⁄₁₈ is the simplest mixed number representation of 25/18, it could also be represented as a decimal (approximately 1.3889). The choice of representation depends on the context and the required level of precision.
Q5: How can I check my answer after converting an improper fraction to a mixed number?
A5: Convert your mixed number back to an improper fraction using the reverse process outlined earlier. If you get the original improper fraction, you have correctly performed the conversion.
Conclusion: Mastering Mixed Numbers
Converting improper fractions, like 25/18, to mixed numbers is a fundamental skill in mathematics. This process combines the principles of division and fraction manipulation to represent quantities in a more easily understandable and usable format. By understanding the steps involved, the underlying mathematical principles, and practicing with various examples, you'll gain confidence and proficiency in working with mixed numbers and improper fractions. This skill will serve as a solid foundation for more advanced mathematical concepts and applications. Remember to practice regularly to solidify your understanding and build your mathematical fluency.
Latest Posts
Latest Posts
-
Solving Exponential Equations Without Logarithms
Sep 23, 2025
-
9 16 Inch In Mm
Sep 23, 2025
-
What Is 760 Mm Science
Sep 23, 2025
-
What Time Is 16 28
Sep 23, 2025
-
All The Factors Of 74
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 25/18 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.