25/6 As A Mixed Number
saludintensiva
Sep 09, 2025 · 6 min read
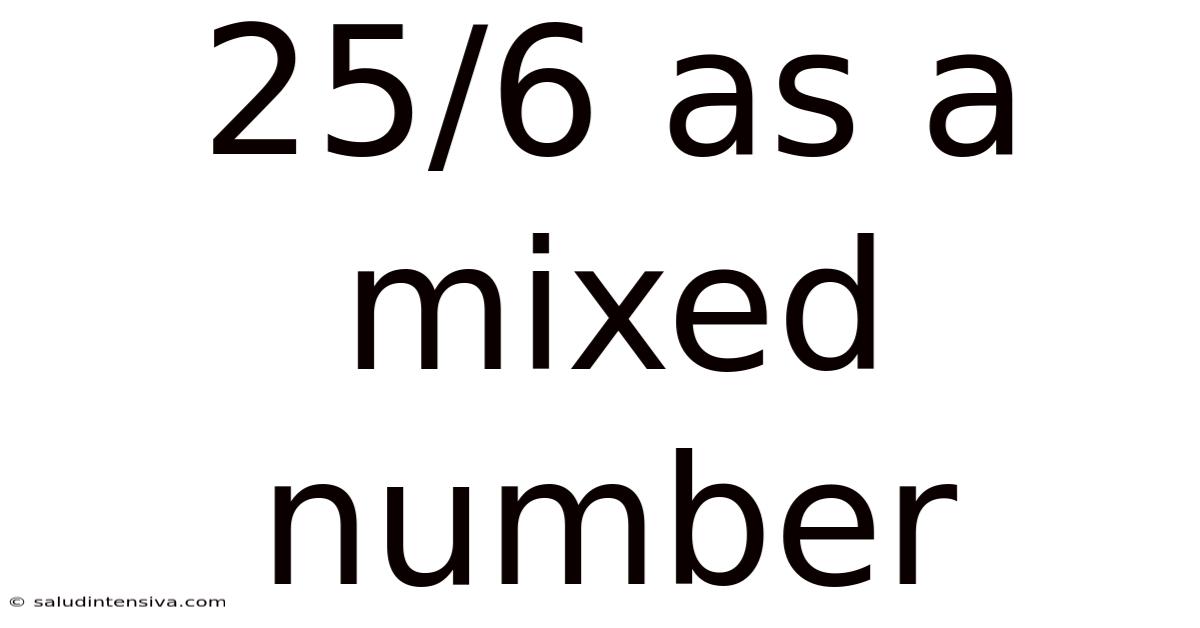
Table of Contents
Understanding 25/6 as a Mixed Number: A Comprehensive Guide
The fraction 25/6 represents a value greater than one. Understanding how to express this as a mixed number – a combination of a whole number and a proper fraction – is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting improper fractions like 25/6 into mixed numbers, exploring the underlying concepts and providing practical examples. We'll also touch upon the importance of this skill in various mathematical applications and address frequently asked questions.
What is a Mixed Number?
Before we dive into converting 25/6, let's define what a mixed number is. A mixed number is a number that combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity larger than one.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 25/6 is an improper fraction because 25 (the numerator) is larger than 6 (the denominator). To convert an improper fraction to a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is.
This can be achieved through division. Let's apply this to 25/6:
-
Divide the numerator by the denominator: 25 ÷ 6 = 4 with a remainder of 1.
-
The quotient (the whole number result of the division) becomes the whole number part of the mixed number: In our case, the quotient is 4.
-
The remainder becomes the numerator of the proper fraction: The remainder is 1.
-
The denominator remains the same: The denominator remains 6.
Therefore, 25/6 as a mixed number is 4 1/6.
Visual Representation of 25/6
Imagine you have 25 equally sized pieces of pizza. If each whole pizza has 6 slices, how many whole pizzas can you make and how many slices will be left over? You can make 4 whole pizzas (4 x 6 = 24 slices), and you'll have 1 slice left over. This visually represents 4 1/6.
The Importance of Converting Improper Fractions to Mixed Numbers
The conversion of improper fractions to mixed numbers is crucial for several reasons:
-
Easier understanding: Mixed numbers are often easier to understand and visualize than improper fractions. It's simpler to grasp the concept of 4 1/6 pizzas than 25/6 pizzas.
-
Real-world applications: Many real-world measurements and quantities are expressed using mixed numbers. For instance, you might measure a length as 2 ½ feet or bake a cake using 1 ¾ cups of flour.
-
Simplification of calculations: In some calculations, working with mixed numbers can be more straightforward than working with improper fractions. For example, adding or subtracting mixed numbers is sometimes easier than adding or subtracting improper fractions.
-
Improved problem-solving: The ability to convert between improper fractions and mixed numbers is essential for solving various mathematical problems, especially in areas like geometry, measurement, and algebra.
Further Examples of Improper Fraction to Mixed Number Conversion
Let's explore a few more examples to solidify your understanding:
-
17/3: 17 ÷ 3 = 5 with a remainder of 2. Therefore, 17/3 = 5 ⅔.
-
22/5: 22 ÷ 5 = 4 with a remainder of 2. Therefore, 22/5 = 4 ⅖.
-
31/8: 31 ÷ 8 = 3 with a remainder of 7. Therefore, 31/8 = 3 ⅞.
-
100/12: 100 ÷ 12 = 8 with a remainder of 4. Therefore, 100/12 = 8 ⁴⁄₁₂ which can be simplified to 8⅓
Converting Mixed Numbers back to Improper Fractions
It’s equally important to understand the reverse process: converting a mixed number back into an improper fraction. This skill is crucial for performing certain calculations more efficiently. The process involves the following steps:
-
Multiply the whole number by the denominator: For example, in 4 1/6, multiply 4 by 6, which equals 24.
-
Add the numerator to the result: Add the numerator (1) to the result from step 1 (24), giving 25.
-
Keep the denominator the same: The denominator remains 6.
Therefore, 4 1/6 converts back to 25/6.
Working with Mixed Numbers in Calculations
Adding, subtracting, multiplying, and dividing mixed numbers requires specific steps. Let's briefly look at addition and subtraction:
Addition of Mixed Numbers:
To add mixed numbers, you can either convert them to improper fractions first or add the whole numbers and the fractions separately, simplifying the result if needed.
Example: 2 ½ + 1 ⅓ = (2 + 1) + (½ + ⅓) = 3 + (3/6 + 2/6) = 3 + 5/6 = 3 ⁵⁄₆
Subtraction of Mixed Numbers:
Subtraction of mixed numbers similarly involves either converting to improper fractions or subtracting the whole numbers and fractions separately. Sometimes, you might need to borrow from the whole number if the fraction in the minuend (the number being subtracted from) is smaller than the fraction in the subtrahend (the number being subtracted).
Example: 4 ⅓ - 1 ⅔ = (4 - 1) + (⅓ - ⅔) = 3 + (1/3 - 2/3) = 3 - ⅓ = 2 ⅔ (you need to borrow 1 from the 3, making it 2 and adding 3/3 to the 1/3)
Frequently Asked Questions (FAQ)
Q: Why is it important to learn about mixed numbers?
A: Mixed numbers provide a more intuitive and practical way to represent quantities larger than one in many real-world scenarios, simplifying calculations and comprehension.
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, all improper fractions can be converted into mixed numbers.
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, the improper fraction is already a whole number. For instance, 12/3 = 4.
Q: How do I simplify a mixed number?
A: Simplify the fraction part of the mixed number to its lowest terms. For example, 4 ⁶⁄₁₂ simplifies to 4 ½ because 6/12 simplifies to ½.
Q: Are there different ways to represent the same value using fractions and mixed numbers?
A: Yes, for example, 25/6, 4 1/6, and other equivalent fractions (like 50/12) all represent the same quantity.
Conclusion
Converting an improper fraction like 25/6 to its mixed number equivalent, 4 1/6, is a fundamental skill in arithmetic. Understanding this conversion process is essential not only for solving mathematical problems but also for applying mathematical concepts in real-world situations. The ability to comfortably work with both improper fractions and mixed numbers is a key element of numeracy, paving the way for more advanced mathematical concepts and problem-solving skills. Through practice and understanding the underlying principles, this concept becomes an intuitive and easily manageable part of your mathematical toolkit.
Latest Posts
Latest Posts
-
1 15 In Decimal Form
Sep 10, 2025
-
12 3 4 As A Decimal
Sep 10, 2025
-
4 9 Simplified As A Fraction
Sep 10, 2025
-
Military Time Minute Conversion Chart
Sep 10, 2025
-
Is 1 2 Greater Than 1 3
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 25/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.