27/2 As A Mixed Number
saludintensiva
Sep 17, 2025 · 6 min read
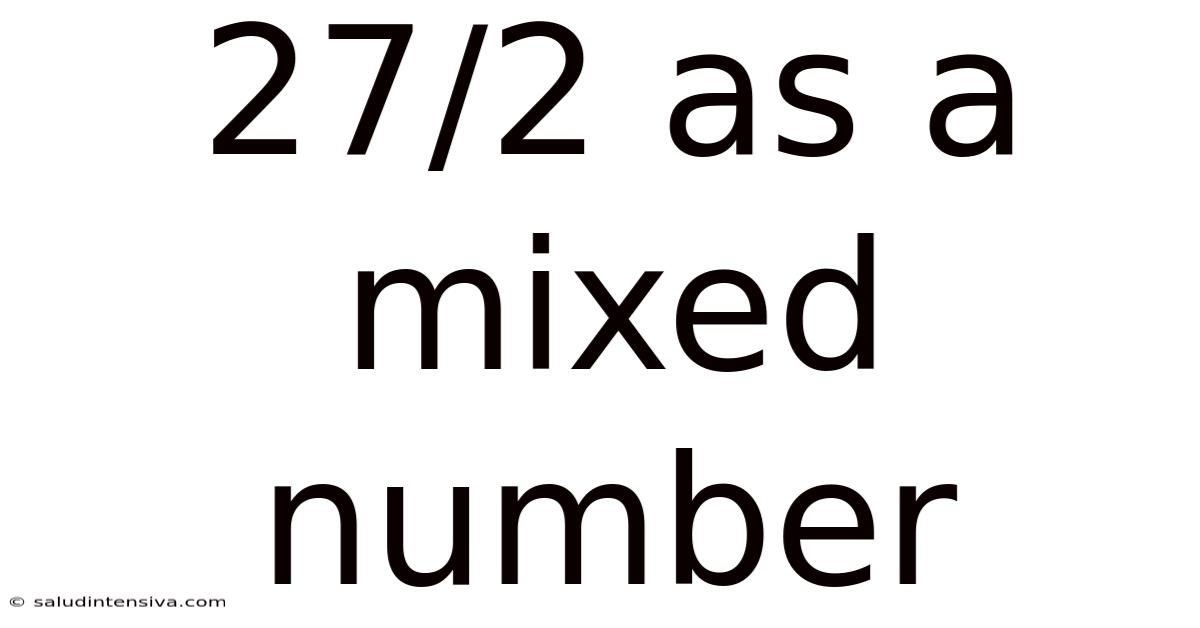
Table of Contents
Understanding 27/2 as a Mixed Number: A Comprehensive Guide
The fraction 27/2 represents a value greater than one. Understanding how to convert it to a mixed number – a combination of a whole number and a proper fraction – is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 27/2 to a mixed number, but also why this conversion is useful and explore the broader mathematical concepts involved. We'll also delve into related topics and address frequently asked questions, providing a complete understanding of this crucial mathematical concept.
What is a Mixed Number?
Before we dive into converting 27/2, let's define what a mixed number is. A mixed number is a number expressed as the sum of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾ is a mixed number; 1 is the whole number, and ¾ is the proper fraction. Mixed numbers are a convenient way to represent values that are greater than one but not a whole number. They offer a more intuitive understanding than improper fractions (like 27/2) in many real-world applications.
Converting 27/2 to a Mixed Number: Step-by-Step
Converting an improper fraction like 27/2 to a mixed number involves dividing the numerator by the denominator. Here's a step-by-step guide:
-
Divide the numerator by the denominator: Divide 27 by 2. This gives you a quotient (the result of the division) and a remainder.
27 ÷ 2 = 13 with a remainder of 1
-
Identify the whole number: The quotient (13) becomes the whole number part of your mixed number.
-
Identify the fraction: The remainder (1) becomes the numerator of the fraction, and the denominator remains the same (2). This gives you the fraction 1/2.
-
Combine the whole number and the fraction: Combine the whole number and the fraction to create the mixed number.
Therefore, 27/2 as a mixed number is 13 ½.
Visual Representation: Understanding the Conversion
Imagine you have 27 slices of pizza, and you want to divide them into groups of 2 slices each. You can make 13 complete groups of 2 slices (13 x 2 = 26 slices). You'll have 1 slice left over. This leftover slice represents the remaining fraction (1/2). Therefore, you have 13 whole pizzas and one half of a pizza, which is represented as 13 ½. This visual representation helps solidify the understanding of the conversion process.
The Importance of Mixed Numbers
Mixed numbers are essential for several reasons:
-
Real-world applications: Many real-world measurements and quantities are best represented using mixed numbers. For example, measuring the length of a piece of wood as 3 ½ feet is much more intuitive than expressing it as 7/2 feet.
-
Simplification: Mixed numbers often provide a more concise and easily understandable representation of a quantity compared to improper fractions. They are easier to visualize and work with in everyday situations.
-
Calculations: While addition and subtraction of mixed numbers might seem more complex at first glance, they often offer a simpler approach than working with improper fractions, especially when dealing with larger numbers.
-
Understanding proportions: Mixed numbers help visualize proportions more clearly. For instance, understanding that 2 1/3 represents two whole units plus one-third of a unit offers a better understanding of the magnitude than the equivalent improper fraction 7/3.
Further Exploration: Working with Mixed Numbers
Once you understand how to convert an improper fraction to a mixed number, you can explore more complex operations:
-
Adding and subtracting mixed numbers: This involves either converting the mixed numbers to improper fractions, performing the operation, and then converting the result back to a mixed number, or working directly with the whole numbers and fractions separately.
-
Multiplying and dividing mixed numbers: Similarly, you might convert mixed numbers to improper fractions for easier multiplication and division or utilize distributive properties to simplify the calculation.
-
Converting mixed numbers back to improper fractions: The reverse process is also important. To convert a mixed number back to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 13 ½ would become (13 x 2) + 1 = 27/2.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert improper fractions to mixed numbers?
A1: Converting improper fractions to mixed numbers is crucial for understanding and working with fractional quantities effectively. It provides a more intuitive representation of quantities larger than one, improving both comprehension and practical application in various situations.
Q2: Can I use a calculator to convert 27/2 to a mixed number?
A2: While calculators can perform the division (27 ÷ 2), they might not directly show the remainder in a mixed-number format. You still need to understand the process of converting the quotient and remainder into the mixed number format. Many calculators designed for fractional calculations will give you a mixed number result directly.
Q3: Are there any other ways to represent 27/2 besides as a mixed number or an improper fraction?
A3: Yes, 27/2 can also be represented as a decimal (13.5) which shows the numeric value in a different but equally valid format. The best choice of representation (mixed number, improper fraction, or decimal) often depends on the context and the desired level of precision and clarity.
Q4: What if the remainder is zero after dividing the numerator by the denominator?
A4: If the remainder is zero, it means the fraction is already a whole number. There is no fractional part in the mixed number; the result is simply the quotient. For example, if you divide 20 by 5, you get 4 with a remainder of 0; therefore, 20/5 is equal to the whole number 4.
Q5: Can I use this process for any improper fraction?
A5: Yes, the process of dividing the numerator by the denominator and expressing the quotient and remainder as a mixed number applies to any improper fraction. This method is a fundamental technique in working with fractions.
Conclusion
Converting 27/2 to the mixed number 13 ½ is a simple yet essential skill in mathematics. This process involves dividing the numerator by the denominator, using the quotient as the whole number, and the remainder as the numerator of the fraction. Understanding this concept is crucial not only for academic success but also for effective problem-solving in various real-world scenarios. The ability to work comfortably with mixed numbers is fundamental for success in further mathematical studies and practical applications. Mastering this concept opens the door to a deeper understanding of fractions and their importance in our everyday lives. Remember to practice regularly to solidify your understanding and develop confidence in working with fractions and mixed numbers.
Latest Posts
Latest Posts
-
13 As A Fraction Simplified
Sep 17, 2025
-
Lcm Of 18 And 20
Sep 17, 2025
-
Convert 250 Pounds To Kilos
Sep 17, 2025
-
260 Billion In Scientific Notation
Sep 17, 2025
-
Answer To A Multiplication Problem
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 27/2 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.