27/8 As A Mixed Number
saludintensiva
Sep 11, 2025 · 6 min read
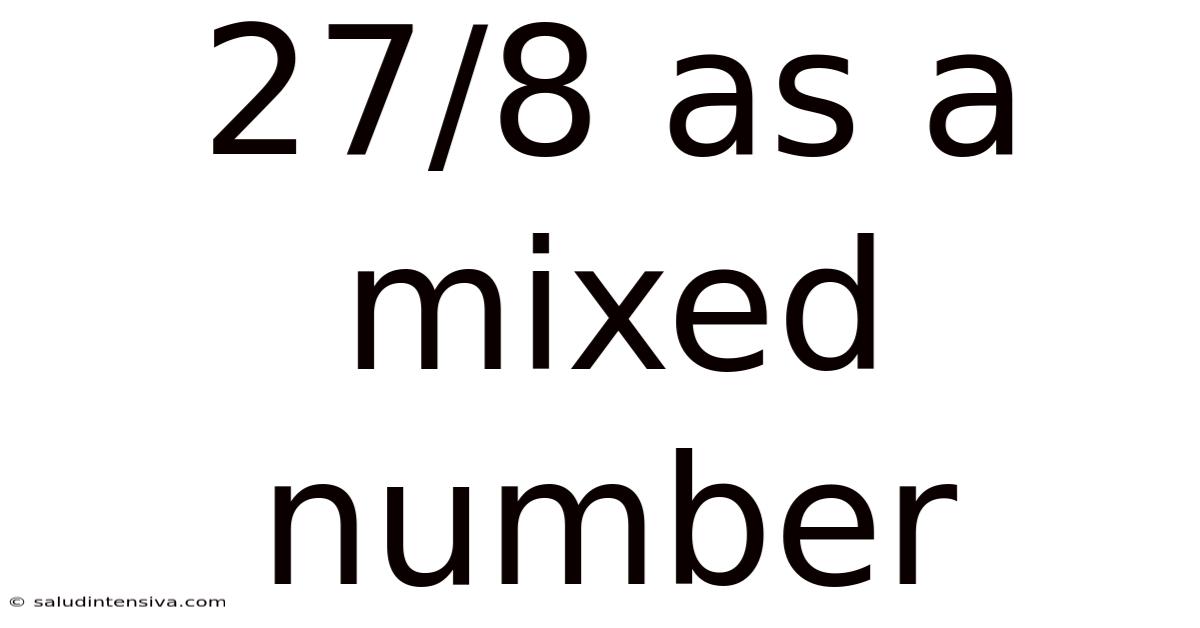
Table of Contents
Understanding 27/8 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 27/8, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 27/8 into a mixed number but will also delve into the underlying concepts, provide practical examples, and address frequently asked questions. Mastering this skill will solidify your understanding of fractions and pave the way for more advanced mathematical concepts.
Introduction to Fractions and Mixed Numbers
Before we dive into converting 27/8, let's refresh our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 27/8, 5/4, 10/10). In contrast, a proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 7/10).
A mixed number combines a whole number and a proper fraction (e.g., 3 ¼, 2 ⅔, 1 ⅛). Mixed numbers are a convenient way to represent improper fractions, making them easier to visualize and work with in practical applications.
Converting 27/8 into a Mixed Number: A Step-by-Step Guide
Now, let's focus on converting the improper fraction 27/8 into a mixed number. The process involves dividing the numerator by the denominator.
Step 1: Divide the numerator by the denominator.
Divide 27 by 8.
27 ÷ 8 = 3 with a remainder of 3.
Step 2: The quotient becomes the whole number part.
The quotient (the result of the division) is 3. This becomes the whole number part of our mixed number.
Step 3: The remainder becomes the numerator of the fraction.
The remainder is 3. This becomes the numerator of the fractional part of our mixed number.
Step 4: The denominator remains the same.
The denominator remains 8.
Step 5: Combine the whole number and the fraction.
Therefore, 27/8 as a mixed number is 3 3/8.
Visualizing the Conversion
Imagine you have 27 slices of pizza, and each pizza has 8 slices. To find out how many whole pizzas you have and how many slices are left over, you would divide 27 by 8. The result, 3 with a remainder of 3, tells you you have 3 whole pizzas (the quotient) and 3 slices left over (the remainder). These 3 leftover slices, out of a possible 8 slices per pizza, represent the fraction 3/8. Hence, you have 3 3/8 pizzas.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Once you've converted an improper fraction to a mixed number, you can then perform various arithmetic operations. Let's briefly explore these:
-
Addition and Subtraction: To add or subtract mixed numbers, you typically convert them back into improper fractions for easier calculation. For example, to add 3 3/8 + 1 ½, you would convert both to improper fractions (27/8 + 3/2), find a common denominator (27/8 + 12/8), and then add the numerators (39/8). This improper fraction can then be converted back to a mixed number (4 7/8).
-
Multiplication: When multiplying mixed numbers, you can either convert them to improper fractions first or use the distributive property. For example, to multiply 3 3/8 * 2, you could convert 3 3/8 to 27/8 and then multiply: (27/8) * 2 = 54/8 = 6 ¾.
-
Division: Similar to multiplication, converting mixed numbers to improper fractions is often the easiest approach for division. For example, to divide 3 3/8 by 1 ½, you would convert them to improper fractions (27/8 ÷ 3/2), invert the second fraction and multiply (27/8 * 2/3), and simplify the result (9/4) or convert it to a mixed number (2 ¼).
Further Exploration: Equivalent Fractions and Simplification
Remember that multiple equivalent fractions can represent the same value. For instance, 27/8 is equivalent to 54/16, 81/24, and many others. However, 3 3/8 is the simplified mixed number representation of 27/8. It's important to simplify fractions to their lowest terms whenever possible to make calculations easier and results clearer. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Practical Applications of Mixed Numbers
Mixed numbers are used extensively in various real-world applications:
-
Cooking and Baking: Recipes often call for mixed numbers for ingredient quantities (e.g., 1 ½ cups of flour).
-
Construction and Engineering: Measurements in construction projects frequently involve mixed numbers (e.g., 2 3/4 inches).
-
Everyday Measurements: We encounter mixed numbers when measuring lengths, weights, and volumes (e.g., 3 1/2 feet, 1 1/4 pounds).
-
Time: Time is often expressed using mixed numbers (e.g., 1 hour and 15 minutes can be represented as 1 ¼ hours).
Frequently Asked Questions (FAQs)
Q1: Why do we use mixed numbers?
Mixed numbers provide a more intuitive and easily understandable representation of quantities compared to improper fractions, particularly in everyday contexts. They clearly show the whole number part and the fractional part, making them more practical for visual representation and interpretation.
Q2: Can all improper fractions be converted into mixed numbers?
Yes, all improper fractions can be converted into mixed numbers. The process of division will always produce a whole number quotient and a remainder that forms the fractional part of the mixed number.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
If the remainder is zero, the improper fraction is already a whole number. For example, 8/8 = 1. There's no fractional part in the mixed number representation; it's simply a whole number.
Q4: How do I convert a mixed number back to an improper fraction?
To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, to convert 3 3/8 back to an improper fraction: (3 * 8) + 3 = 27; the improper fraction is 27/8.
Q5: Are there any shortcuts for converting improper fractions to mixed numbers?
While the long division method is thorough and conceptually sound, some individuals may develop mental shortcuts for common fractions through practice and familiarity. For example, with experience, you might quickly recognize that 27/8 is equivalent to 3 3/8 without formal long division.
Conclusion
Converting improper fractions like 27/8 into mixed numbers is a crucial skill in mathematics. This guide has provided a step-by-step approach, visual aids, and practical examples to help you master this fundamental concept. Remember to practice regularly to build your confidence and proficiency. Understanding mixed numbers will not only enhance your mathematical skills but also equip you with the tools to confidently handle various real-world applications involving fractions. The ability to effortlessly switch between improper fractions and mixed numbers represents a significant step towards a deeper understanding of mathematical principles and their applications.
Latest Posts
Latest Posts
-
How Long Is 5 Minutes
Sep 11, 2025
-
Volume Of A Oblique Cone
Sep 11, 2025
-
37 Degree Fahrenheit To Celsius
Sep 11, 2025
-
What Percent Is 6 9
Sep 11, 2025
-
Change Fraction To Whole Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 27/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.