27 Out Of 30 Percent
saludintensiva
Sep 17, 2025 · 6 min read
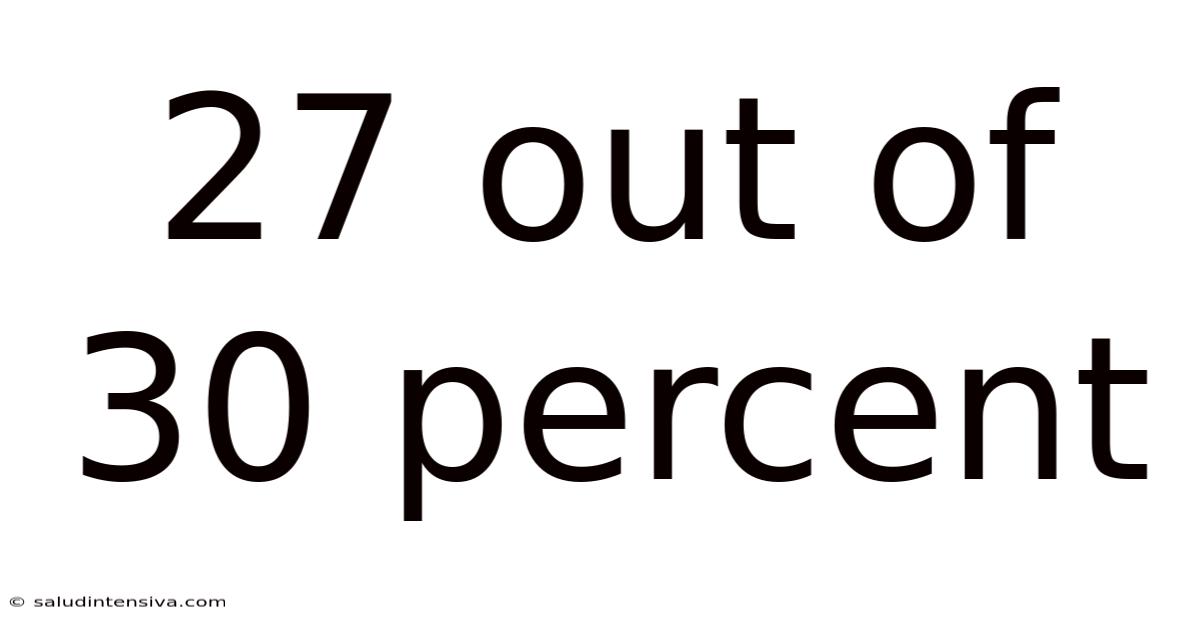
Table of Contents
Decoding 27 out of 30: Understanding Percentages and Their Significance
Understanding percentages is a fundamental skill in various aspects of life, from academic assessments to financial planning. This article delves into the meaning and implications of scoring 27 out of 30, exploring its percentage equivalent, its potential applications, and how to interpret such scores in different contexts. We will also discuss the broader understanding of percentages and their role in everyday calculations. This comprehensive guide will equip you with the tools to confidently interpret and utilize percentage calculations in various situations.
Understanding Percentage Calculations
Before diving into the specifics of 27 out of 30, let's establish a firm grasp of percentage calculations. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." To calculate a percentage, we use the following formula:
(Part / Whole) * 100 = Percentage
In this formula:
- Part: Represents the specific value we are interested in (in our case, 27).
- Whole: Represents the total value (in our case, 30).
- Percentage: The resulting value expressed as a number with a "%" sign.
Calculating the Percentage for 27 out of 30
Applying the formula to our scenario (27 out of 30):
(27 / 30) * 100 = 90%
Therefore, a score of 27 out of 30 represents 90%. This signifies a high level of achievement, indicating strong performance.
Interpreting 90% in Different Contexts
The interpretation of a 90% score varies significantly depending on the context. Let's explore some examples:
1. Academic Assessment: In a classroom setting, 90% often indicates an excellent understanding of the subject matter. It suggests mastery of the concepts and skills tested, likely warranting a high grade (A or A- in many grading systems). However, the specific grading scale used by the institution will ultimately dictate the letter grade.
2. Standardized Tests: The interpretation of 90% on a standardized test depends on the test's difficulty and the distribution of scores among the test takers. While 90% generally suggests strong performance, it's crucial to consider the overall average score and percentile rank to understand how the score compares to others who took the test. A percentile rank will place the score within a range of performance, providing better context than just the percentage itself.
3. Business Metrics: In business, a 90% success rate might indicate a highly effective strategy or process. For example, a 90% conversion rate in marketing implies that 90% of leads are successfully converted into customers, signaling a very successful campaign. In manufacturing, a 90% efficiency rate might indicate minimal waste and highly optimized production processes. However, even in business, benchmarks and industry standards should be used to further contextualize the result.
4. Personal Goals: If 90% represents the completion of a personal goal, it signifies significant progress and a high level of achievement. For instance, if you aimed to read 30 books in a year and managed to read 27, it suggests a consistent commitment to your reading habit. The level of accomplishment should be assessed relative to the individual's personal circumstances and capabilities.
Beyond the Numbers: Understanding Variability and Error
While a 90% score is generally considered excellent, it's crucial to acknowledge the potential for variability and error in any measurement. Several factors can influence scores, including:
-
Test Difficulty: A test that is overly difficult might result in lower scores overall, making a 90% even more impressive. Conversely, an easy test might inflate scores, rendering a 90% less significant.
-
Test Design: The design and structure of the test significantly impact the results. A poorly designed test may not accurately assess knowledge or skills, leading to potentially skewed scores.
-
Individual Performance Variability: A student's performance can fluctuate due to several factors, including stress levels, health, and sleep patterns. A single score, therefore, may not always be a perfectly representative measure of a student’s capabilities.
-
Sampling Error (in larger datasets): When dealing with larger datasets, sampling error needs consideration. The 90% might only represent a subset of the total data, and the true percentage might vary. Margin of error calculations are important for statistical accuracy.
Common Misconceptions about Percentages
Several misconceptions surrounding percentage calculations can lead to misinterpretations. Let's address some of the common ones:
-
Confusing Percentage with Proportion: Percentage represents a proportion out of 100, while proportion is a general comparison of two values, which may not be out of 100.
-
Incorrectly Calculating Percentages of Percentages: It's incorrect to simply add percentages together. For instance, a 10% increase followed by a 10% decrease does not result in no change.
-
Ignoring Context: The meaning of a percentage changes drastically depending on the context in which it is presented. Always consider the whole picture before drawing conclusions.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous, extending far beyond academic assessments. Here are some everyday applications:
-
Financial Calculations: Calculating interest rates, discounts, taxes, tips, and investment returns all rely on percentage calculations.
-
Data Analysis: Percentages are essential tools in analyzing data, summarizing trends, and identifying patterns.
-
Scientific Research: Percentages are used extensively in statistical analysis, experimental design, and data interpretation in various scientific fields.
-
Everyday Life: Calculating sales discounts, understanding nutritional information on food labels, and determining the proportion of ingredients in recipes all involve working with percentages.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage increase or decrease between two numbers?
A: To calculate the percentage increase, subtract the original number from the new number, divide the result by the original number, and multiply by 100. To calculate the percentage decrease, follow the same steps, but the result will be negative.
Q: What is a percentile rank?
A: A percentile rank indicates the percentage of scores that fall below a particular score. For example, a score with a percentile rank of 90 means that the score is higher than 90% of the other scores.
Q: How can I improve my understanding of percentages?
A: Practice regularly with various types of problems, utilize online calculators and resources, and try applying percentage calculations to real-life situations.
Conclusion: The Significance of Understanding Percentages
A score of 27 out of 30, translating to 90%, signifies high performance. However, the significance of this score depends heavily on the context. Understanding percentage calculations and their applications is crucial for navigating various aspects of life, from academic achievement to professional success. By grasping the core concepts and practical applications, you can confidently interpret and utilize percentages in your personal and professional endeavors. Remember to always consider the context and potential variability when interpreting numerical results. The ability to analyze and interpret percentages is a valuable skill that empowers informed decision-making and critical thinking.
Latest Posts
Latest Posts
-
Gcf Of 36 And 30
Sep 17, 2025
-
Meters Per Second To Rpm
Sep 17, 2025
-
Gcf Of 18 And 50
Sep 17, 2025
-
First 10 Multiples Of 7
Sep 17, 2025
-
How Long Is 280 Minutes
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 27 Out Of 30 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.