29/4 As A Mixed Number
saludintensiva
Sep 25, 2025 · 5 min read
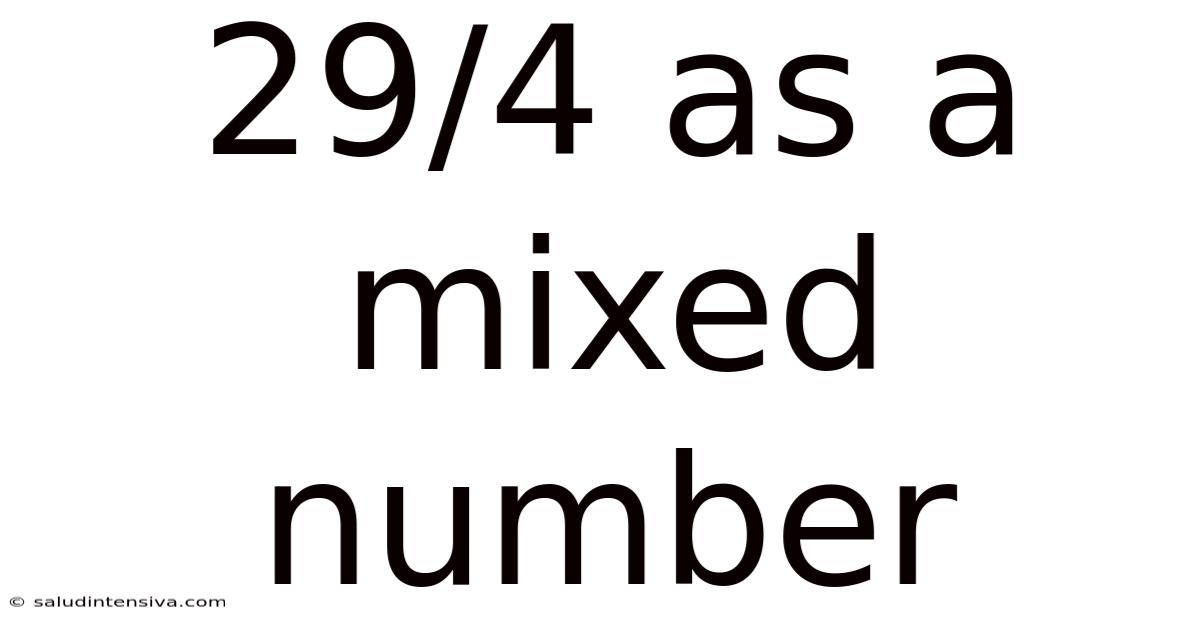
Table of Contents
Understanding 29/4 as a Mixed Number: A Comprehensive Guide
The conversion of improper fractions, like 29/4, into mixed numbers is a fundamental concept in mathematics. This comprehensive guide will not only show you how to convert 29/4 into a mixed number but will also explore the underlying principles, provide practical examples, and delve into the reasons behind this important mathematical operation. Understanding this process is crucial for various mathematical applications, from simple arithmetic to more complex algebraic problems. We'll even tackle some frequently asked questions to ensure you've grasped the concept thoroughly.
What is a Mixed Number?
Before diving into the conversion, let's define what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number, where 2 is the whole number and ¾ is the proper fraction.
Converting 29/4 to a Mixed Number: A Step-by-Step Approach
The core concept behind converting an improper fraction (where the numerator is larger than the denominator) to a mixed number involves determining how many times the denominator goes into the numerator and expressing the remainder as a fraction. Let's break down the process for 29/4:
Step 1: Division
Divide the numerator (29) by the denominator (4).
29 ÷ 4 = 7 with a remainder of 1
Step 2: Identifying the Whole Number and the Fraction
- The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 7.
- The remainder becomes the numerator of the proper fraction. Here, the remainder is 1.
- The denominator of the proper fraction remains the same as the original fraction's denominator. So, the denominator is 4.
Step 3: Combining the Whole Number and the Fraction
Combine the whole number and the proper fraction to form the mixed number.
Therefore, 29/4 as a mixed number is 7 1/4.
Visualizing the Conversion
Imagine you have 29 quarters. Since four quarters make a dollar, you can group your quarters into sets of four. You'll have seven complete sets (7 dollars) and one quarter left over. This visually represents the 7 whole numbers and the remaining 1/4.
Why Convert to Mixed Numbers?
Converting improper fractions to mixed numbers often makes it easier to:
- Understand quantities: Mixed numbers provide a more intuitive understanding of quantities, especially in real-world contexts. Saying you have 7 1/4 dollars is clearer than saying you have 29/4 dollars.
- Compare fractions: Comparing mixed numbers is often simpler than comparing improper fractions. For instance, comparing 7 1/4 and 6 3/4 is straightforward.
- Perform calculations: In some calculations, using mixed numbers can simplify the process and reduce errors. Adding or subtracting mixed numbers can be more intuitive than adding or subtracting improper fractions.
Further Examples of Improper Fraction to Mixed Number Conversion
Let's look at a few more examples to solidify your understanding:
- 17/3: 17 ÷ 3 = 5 with a remainder of 2. Therefore, 17/3 = 5 2/3
- 25/6: 25 ÷ 6 = 4 with a remainder of 1. Therefore, 25/6 = 4 1/6
- 31/5: 31 ÷ 5 = 6 with a remainder of 1. Therefore, 31/5 = 6 1/5
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand how to convert a mixed number back into an improper fraction. This is often necessary when performing multiplication or division of fractions. The process is as follows:
- Multiply the whole number by the denominator: For 7 1/4, this would be 7 x 4 = 28.
- Add the numerator: Add the result from step 1 to the numerator of the fraction: 28 + 1 = 29.
- Keep the denominator the same: The denominator remains 4.
Therefore, 7 1/4 converts back to 29/4. This demonstrates the reversible nature of the conversion process.
The Importance of Understanding Fractions and Mixed Numbers
A solid grasp of fractions and mixed numbers is essential for success in various areas of mathematics and beyond. It forms the foundation for understanding:
- Decimals: Fractions and mixed numbers are directly related to decimals, providing alternative ways to represent the same quantities.
- Ratio and Proportion: The principles of fractions are fundamental to understanding ratios and proportions, crucial in various fields like cooking, construction, and science.
- Algebra: Solving algebraic equations often involves working with fractions and mixed numbers.
- Geometry: Calculating areas, volumes, and other geometrical properties often requires working with fractions.
Frequently Asked Questions (FAQ)
Q1: What if the remainder is zero after dividing the numerator by the denominator?
A1: If the remainder is zero, it means the original fraction is a whole number. For example, 12/4 = 3. There is no fractional part.
Q2: Can negative numbers be involved in mixed numbers?
A2: Yes, both the whole number and the fractional part of a mixed number can be negative. For example, -2 1/3 represents -7/3.
Q3: Is there a shortcut for converting large improper fractions to mixed numbers?
A3: While there's no universally faster method than long division, practicing mental math techniques and familiarity with multiplication tables can significantly speed up the process.
Q4: Why is it important to simplify the fraction part of the mixed number?
A4: Simplifying the fractional part ensures the mixed number is expressed in its simplest form. For instance, 7 2/6 should be simplified to 7 1/3. This improves clarity and consistency.
Q5: Are there different ways to represent the same mixed number?
A5: No, a given mixed number has only one simplified equivalent. While the improper fraction equivalent might have different representations (e.g., 6/2 = 12/4 = 3), the simplified mixed number is unique.
Conclusion
Converting improper fractions to mixed numbers is a vital skill in mathematics. This process, while seemingly simple, underpins a deeper understanding of numerical representation and lays the groundwork for more advanced mathematical concepts. By mastering this conversion and understanding its implications, you'll be better equipped to tackle various mathematical challenges and apply these skills to real-world problems. Remember, practice is key; the more you work with fractions and mixed numbers, the more intuitive and efficient this process will become. Don't hesitate to revisit this guide and work through further examples to reinforce your understanding. The ability to confidently convert between improper fractions and mixed numbers is a significant milestone in your mathematical journey.
Latest Posts
Latest Posts
-
Yard To Meter Conversion Swimming
Sep 25, 2025
-
Convert 14 Millimeters To Inches
Sep 25, 2025
-
3 8 R 2 3
Sep 25, 2025
-
50 Vietnamese Dong To Usd
Sep 25, 2025
-
Gcf Of 28 And 18
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 29/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.