29 6 As A Decimal
saludintensiva
Sep 18, 2025 · 5 min read
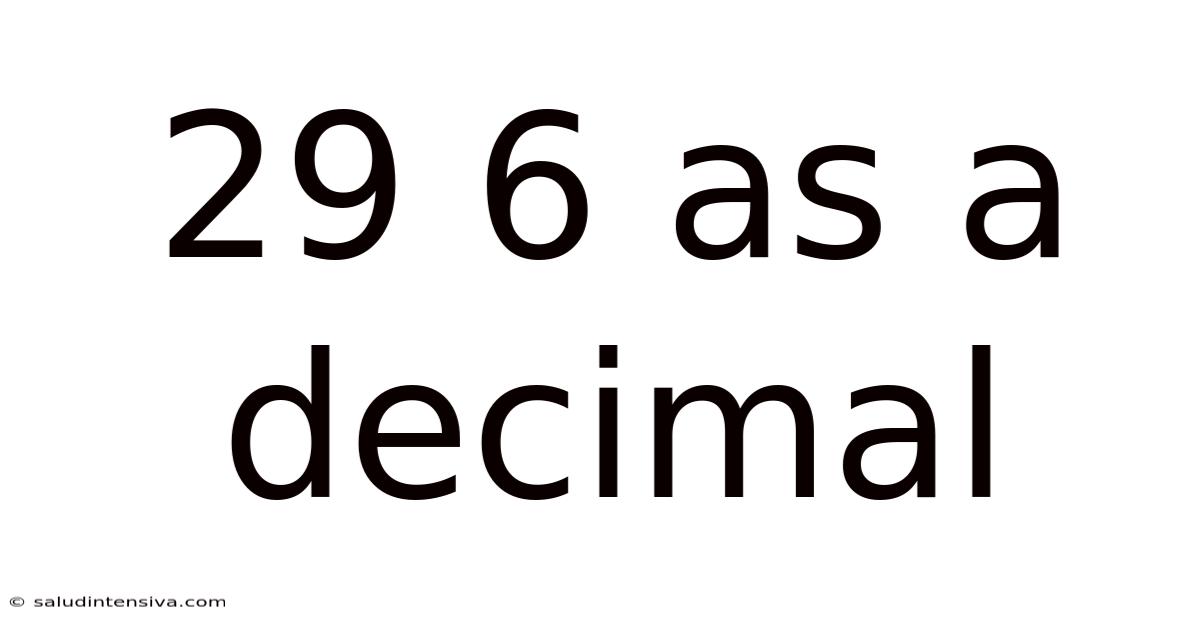
Table of Contents
Unveiling the Mystery: 29/6 as a Decimal
Understanding fractions and their decimal equivalents is a cornerstone of mathematical literacy. This comprehensive guide delves into the conversion of the fraction 29/6 into its decimal form, exploring various methods, underlying principles, and practical applications. We'll move beyond a simple answer, providing you with a deep understanding of the process and its significance in broader mathematical contexts. This will equip you with the skills to confidently tackle similar conversions and solidify your grasp of fractional and decimal representations.
Understanding Fractions and Decimals
Before diving into the conversion of 29/6, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 29/6, 29 is the numerator and 6 is the denominator. This means we have 29 parts out of a total of 6 parts.
A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. Decimals are essentially fractions where the denominator is a power of 10 (10, 100, 1000, etc.). For instance, 0.5 is equivalent to 5/10, and 0.25 is equivalent to 25/100.
The conversion between fractions and decimals involves finding the equivalent decimal representation of a given fraction. This is often necessary for calculations, comparisons, or simply for a clearer representation of a quantity.
Method 1: Long Division
The most straightforward method for converting 29/6 to a decimal is through long division. We divide the numerator (29) by the denominator (6):
4.8333...
6 | 29.0000
-24
50
-48
20
-18
20
-18
20
-18
2...
As you can see, the division results in a repeating decimal: 4.8333... The remainder of 2 continues to reappear, leading to an infinite repetition of the digit 3. This is denoted as 4.8̅3̅. The bar above the 3 indicates the repeating part of the decimal.
Method 2: Converting to a Mixed Number
Another approach involves converting the improper fraction 29/6 into a mixed number. A mixed number combines a whole number and a fraction. To do this, we perform the division:
29 ÷ 6 = 4 with a remainder of 5.
This means 29/6 can be written as 4 5/6. Now, we only need to convert the fractional part, 5/6, into a decimal:
0.8333...
6 | 5.0000
-48
20
-18
20
-18
20
-18
2...
Adding the whole number part, we get 4 + 0.8333... = 4.8333..., or 4.8̅3̅.
Method 3: Using a Calculator
For quick conversions, a calculator is a convenient tool. Simply divide 29 by 6. Most calculators will display the result as 4.833333... Again, this highlights the repeating decimal nature of the result.
Understanding Repeating Decimals
The result of 29/6, 4.8̅3̅, is a repeating decimal. This means the decimal part has a sequence of digits that repeats infinitely. Understanding repeating decimals is crucial in many mathematical applications. They are often represented using a bar above the repeating digits, as shown above. This notation is more concise than writing out an endless string of digits.
Significance of the Result
The conversion of 29/6 to its decimal equivalent, 4.8̅3̅, demonstrates the relationship between fractional and decimal representations. This conversion is important for several reasons:
- Calculations: Decimals are often easier to work with in calculations, particularly when using computers or calculators.
- Comparisons: Comparing decimals is generally simpler than comparing fractions, especially when dealing with unlike denominators.
- Real-world applications: Many real-world measurements and quantities are expressed as decimals, such as prices, lengths, and weights. Converting fractions to decimals allows for easier integration with these systems.
- Understanding Number Systems: This process helps reinforce the understanding of different number systems and their inter-relationships.
Practical Applications
Converting fractions to decimals finds applications in various fields:
- Finance: Calculating interest rates, discounts, or profit margins often involves converting fractions to decimals.
- Engineering: Precision measurements and calculations in engineering rely heavily on the use of decimals.
- Science: Many scientific calculations and data representations utilize decimals for accuracy and clarity.
- Everyday Life: From calculating tips to measuring ingredients in cooking, understanding decimals is essential for everyday tasks.
Frequently Asked Questions (FAQ)
Q: Why is 29/6 a repeating decimal?
A: A fraction results in a repeating decimal when the denominator contains prime factors other than 2 and 5 (the prime factors of 10). Since the denominator of 29/6 is 6 (which has prime factors of 2 and 3), it results in a repeating decimal.
Q: Can all fractions be converted to terminating decimals?
A: No. Only fractions whose denominators have only 2 and/or 5 as prime factors can be converted to terminating decimals. Other fractions will result in repeating decimals.
Q: How do I round a repeating decimal?
A: You can round a repeating decimal to a specific number of decimal places based on your required accuracy. For instance, 4.8̅3̅ can be rounded to 4.83, 4.833, 4.8333, and so on, depending on the desired level of precision.
Q: Are there any other methods to convert 29/6 to a decimal?
A: While long division and converting to a mixed number are the most common and fundamental methods, more advanced techniques exist involving continued fractions or other algebraic manipulations. However, for this specific problem, long division or the mixed number approach are the most efficient.
Conclusion
Converting 29/6 to its decimal equivalent, 4.8̅3̅, is a fundamental mathematical skill with broad applications. This guide provided a step-by-step explanation of different methods, highlighted the significance of repeating decimals, and explored practical applications across various fields. Understanding the principles behind this conversion solidifies your understanding of fractions, decimals, and their interrelationship, empowering you to tackle similar conversions with confidence and precision. Mastering this skill is essential for anyone seeking a strong foundation in mathematics and its practical applications. Remember, practice is key to mastering these concepts, so keep practicing!
Latest Posts
Latest Posts
-
Ones Tens Hundreds Thousands Chart
Sep 18, 2025
-
1 3 To The Second Power
Sep 18, 2025
-
7 4 As A Fraction
Sep 18, 2025
-
3 4 Plus 1 4
Sep 18, 2025
-
32 Deg C To Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 29 6 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.