2x 2 13x 15 Factor
saludintensiva
Sep 24, 2025 · 6 min read
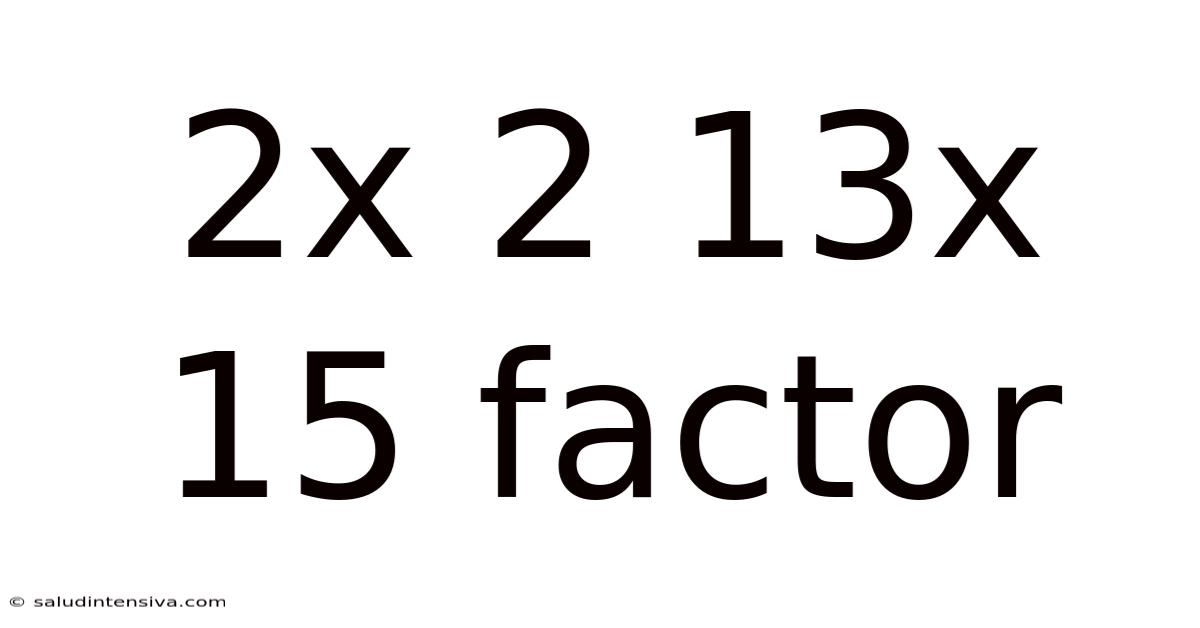
Table of Contents
Decoding the Factors of 2 x 2 x 13 x 15: A Deep Dive into Prime Factorization and Beyond
Understanding the factors of a number is fundamental to grasping various mathematical concepts. This article delves into the complete factorization of 2 x 2 x 13 x 15, exploring not only the basic factors but also the underlying principles of prime factorization, greatest common divisor (GCD), least common multiple (LCM), and their practical applications. This comprehensive guide aims to provide a clear, step-by-step explanation suitable for learners of all levels, from beginners grappling with basic multiplication to those seeking a deeper understanding of number theory.
Introduction: Prime Factorization – The Building Blocks of Numbers
Before we embark on factoring 2 x 2 x 13 x 15, let's establish a strong foundation. The cornerstone of factorization is the concept of prime numbers. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, and so on. Prime factorization is the process of expressing a number as a product of its prime factors. This representation is unique for every number (excluding 0 and 1). This uniqueness is crucial for numerous mathematical operations.
Step-by-Step Factorization of 2 x 2 x 13 x 15
Our target expression is 2 x 2 x 13 x 15. Let's break down each factor into its prime components:
- 2: This is already a prime number.
- 2: Again, a prime number.
- 13: This is also a prime number.
- 15: This is a composite number (a number that is not prime). We can factor it as 3 x 5, both of which are prime numbers.
Therefore, the complete prime factorization of 2 x 2 x 13 x 15 is 2 x 2 x 3 x 5 x 13. We can also represent this more concisely using exponents as 2² x 3 x 5 x 13. This representation shows that the number is composed of two 2s, one 3, one 5, and one 13.
Identifying all Factors
Now that we have the prime factorization, we can systematically determine all the factors of the number 2 x 2 x 13 x 15 = 780. To do this, we consider all possible combinations of the prime factors:
- Combinations of single factors: 2, 3, 5, 13
- Combinations of two factors: 2 x 2 = 4, 2 x 3 = 6, 2 x 5 = 10, 2 x 13 = 26, 3 x 5 = 15, 3 x 13 = 39, 5 x 13 = 65
- Combinations of three factors: 2 x 2 x 3 = 12, 2 x 2 x 5 = 20, 2 x 2 x 13 = 52, 2 x 3 x 5 = 30, 2 x 3 x 13 = 78, 2 x 5 x 13 = 130, 3 x 5 x 13 = 195
- Combinations of four factors: 2 x 2 x 3 x 5 = 60, 2 x 2 x 3 x 13 = 156, 2 x 2 x 5 x 13 = 260, 2 x 3 x 5 x 13 = 390
- Combination of all five factors: 2 x 2 x 3 x 5 x 13 = 780
Therefore, the complete list of factors for 780 is: 1, 2, 3, 4, 5, 6, 10, 12, 13, 15, 20, 26, 30, 39, 52, 60, 65, 78, 130, 156, 195, 260, 390, and 780. Notice that 1 and 780 are also included as factors; every number is divisible by 1 and itself.
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
The prime factorization method is also invaluable in calculating the GCD and LCM of multiple numbers.
Let's consider finding the GCD and LCM of two numbers, say 780 (our original number) and another number, let's choose 390.
- Prime factorization of 390: 2 x 3 x 5 x 13
GCD: To find the GCD, we identify the common prime factors in both numbers and multiply them together with the lowest power present. Both 780 (2² x 3 x 5 x 13) and 390 (2 x 3 x 5 x 13) share 2, 3, 5, and 13. The lowest power of 2 is 2¹. Therefore, the GCD(780, 390) = 2 x 3 x 5 x 13 = 390.
LCM: To find the LCM, we identify all the prime factors present in either number and multiply them together with the highest power present. In our case, we have 2², 3, 5, and 13. Therefore, the LCM(780, 390) = 2² x 3 x 5 x 13 = 780.
Applications in Real-World Scenarios
The seemingly abstract concepts of prime factorization, GCD, and LCM find practical applications in diverse fields:
- Cryptography: Prime factorization forms the basis of many modern encryption algorithms, ensuring secure data transmission.
- Computer Science: Understanding factors is essential in optimizing algorithms and data structures.
- Engineering: Calculations involving ratios and proportions often rely on GCD and LCM.
- Music Theory: Understanding ratios and their simplification using GCD plays a crucial role in harmonic relationships.
Frequently Asked Questions (FAQ)
Q1: What is the significance of prime factorization?
A1: Prime factorization provides a unique and fundamental representation of a number, crucial for various mathematical operations, including finding GCD and LCM, simplifying fractions, and understanding number properties.
Q2: Can a number have more than one prime factorization?
A2: No, the Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors).
Q3: How do I find the factors of a larger number easily?
A3: The most efficient method is to find the prime factorization. Once you have the prime factorization, you can systematically generate all factors by considering all possible combinations of the prime factors.
Q4: What if a number is already in its prime factorized form?
A4: If a number is already in its prime factorized form, you've already completed the factorization process. You can then easily proceed to determine its factors or use it to calculate GCD and LCM with other numbers.
Q5: Are there any shortcuts for finding factors?
A5: While there aren't universal shortcuts, observing divisibility rules (for 2, 3, 5, etc.) can speed up the initial stages of finding factors. However, for larger numbers, prime factorization remains the most reliable and systematic approach.
Conclusion: Beyond the Basics of Factorization
This article has provided a comprehensive exploration of the factors of 2 x 2 x 13 x 15, going beyond a simple answer to delve into the fundamental concepts underlying number theory. Understanding prime factorization is not just about finding factors; it's about unlocking a deeper understanding of numbers and their properties. This knowledge serves as a cornerstone for more advanced mathematical concepts and finds practical application in various fields. By mastering these concepts, you equip yourself with powerful tools for tackling a wide range of mathematical challenges. Remember, the key is to approach these concepts systematically and practice regularly. The more you engage with these ideas, the more intuitive and rewarding they will become.
Latest Posts
Latest Posts
-
What Is 2 3 Of 17
Sep 24, 2025
-
How To Divide By Ratio
Sep 24, 2025
-
4 Times What Equals 60
Sep 24, 2025
-
How Many 1 8 Make 1 4
Sep 24, 2025
-
What Is The Cumulative Percentage
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 13x 15 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.