3 1 As A Percentage
saludintensiva
Sep 17, 2025 · 5 min read
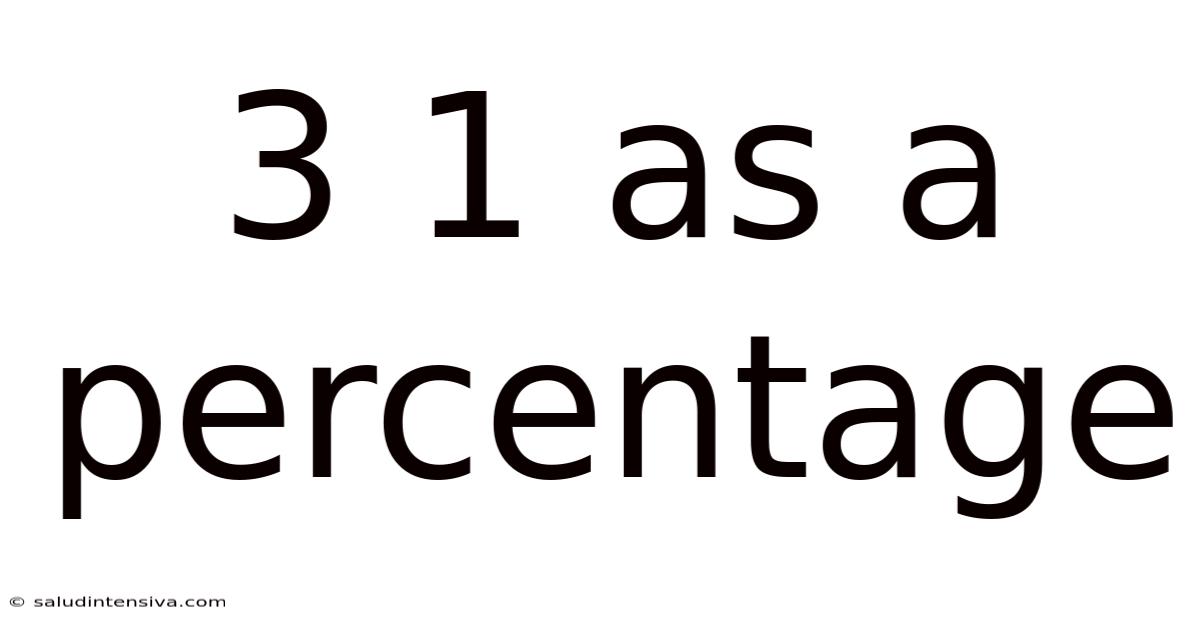
Table of Contents
Understanding 3/1 as a Percentage: A Comprehensive Guide
Representing fractions as percentages is a fundamental skill in mathematics, crucial for various applications from everyday budgeting to complex scientific calculations. This article provides a comprehensive guide to understanding how to convert the fraction 3/1 into a percentage, explaining the underlying principles and offering practical examples to solidify your understanding. We will delve into the meaning of fractions, percentages, and the conversion process, ensuring a clear and thorough comprehension of this essential mathematical concept. This guide will also cover related concepts and address frequently asked questions, making it a valuable resource for students and anyone looking to improve their mathematical skills.
What is a Fraction?
Before we dive into converting 3/1 into a percentage, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It is written in the form a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). For example, in the fraction 1/4, 1 represents one part out of a total of 4 parts.
What is a Percentage?
A percentage is simply a fraction expressed as parts per hundred. It represents a proportion out of 100. The symbol "%" is used to denote a percentage. For instance, 50% means 50 parts out of 100, which is equivalent to the fraction 50/100, or the simplified fraction 1/2.
Converting Fractions to Percentages: The Method
The process of converting a fraction to a percentage involves two main steps:
- Convert the fraction to a decimal: This involves dividing the numerator by the denominator.
- Convert the decimal to a percentage: This is done by multiplying the decimal by 100 and adding the percentage symbol (%).
Let's apply this method to the fraction 3/1:
Step 1: Convert the fraction to a decimal.
3 ÷ 1 = 3
Step 2: Convert the decimal to a percentage.
3 x 100% = 300%
Understanding the Result: 300%
The result, 300%, might seem surprising at first. It's important to understand what this represents. A percentage greater than 100% indicates that the "part" is larger than the "whole." In the case of 3/1, the numerator (3) is three times larger than the denominator (1). This means that the fraction represents 300% of the whole. Imagine you have a pizza. The fraction 3/1 represents having three whole pizzas – three times the amount of one pizza. Therefore, it is 300% of one pizza.
Practical Applications of Percentages Greater Than 100%
Percentages exceeding 100% are commonly used in various contexts:
- Business and Finance: Growth percentages often surpass 100%. For example, if a company's profits increase from $1 million to $3 million, the percentage increase is 200%.
- Science and Statistics: Increases in populations, quantities, or measurements can exceed 100%. For instance, if a bacterial colony triples in size, its growth is 200%.
- Data Analysis and Reporting: In comparing different data sets, percentages over 100% can be used to showcase significant increases or discrepancies.
Alternative Methods for Converting Fractions to Percentages
While the method described above is the most straightforward, there are alternative approaches, particularly useful when dealing with more complex fractions.
Method 1: Using Equivalent Fractions
This method involves finding an equivalent fraction with a denominator of 100. For simple fractions, this can be a quick and efficient method. However, it becomes less practical with more complex fractions.
In our case of 3/1, we would multiply both the numerator and the denominator by 100 to obtain an equivalent fraction with a denominator of 100:
(3 x 100) / (1 x 100) = 300/100
Since 300/100 means 300 parts out of 100, this directly translates to 300%.
Method 2: Using Proportions
This method is particularly helpful when dealing with fractions that don't easily convert to a denominator of 100. It involves setting up a proportion:
x/100 = 3/1
To solve for x, cross-multiply:
1x = 300
Therefore, x = 300, indicating that 3/1 is equivalent to 300%.
Further Exploration: Working with Different Fractions
Let's consider other examples to reinforce the understanding of fraction-to-percentage conversions:
- 1/2: 1 ÷ 2 = 0.5 ; 0.5 x 100% = 50%
- 2/5: 2 ÷ 5 = 0.4 ; 0.4 x 100% = 40%
- 7/4: 7 ÷ 4 = 1.75 ; 1.75 x 100% = 175%
These examples highlight the versatility of the conversion process, accommodating both fractions less than and greater than 1.
Frequently Asked Questions (FAQ)
Q1: What does it mean when a percentage is greater than 100%?
A: A percentage greater than 100% indicates that the value being represented is more than the whole or the base value. It signifies an increase exceeding the initial value.
Q2: Can all fractions be converted into percentages?
A: Yes, all fractions can be converted into percentages. The process involves dividing the numerator by the denominator and then multiplying the result by 100%.
Q3: What if the fraction involves decimals?
A: The process remains the same. Divide the numerator by the denominator and multiply the result by 100%. For example, 0.5/1 = 0.5; 0.5 x 100% = 50%.
Q4: Are there any limitations to using percentages?
A: While percentages are useful, they can sometimes be misleading. It's crucial to understand the context and the base value being used. Without context, a percentage on its own may not provide a complete picture.
Q5: What are some real-world applications of converting fractions to percentages?
A: Converting fractions to percentages is used extensively in numerous fields, including:
- Calculating discounts and sales tax
- Determining grades and test scores
- Analyzing financial data and market trends
- Representing proportions in scientific research
- Calculating interest rates and loan repayments
Conclusion
Converting fractions to percentages is a fundamental skill with broad applications. Understanding the process, particularly when dealing with percentages greater than 100%, is vital for accurate interpretation and effective communication of quantitative information. The methods outlined in this article provide a robust foundation for mastering this essential mathematical concept, allowing you to confidently tackle diverse problems involving fractions and percentages in various academic and professional settings. Remember, practice is key. The more you practice converting fractions to percentages, the more comfortable and proficient you will become. Don't hesitate to work through various examples to solidify your understanding and build confidence in this crucial mathematical skill.
Latest Posts
Latest Posts
-
The Difference Of Two Squares
Sep 17, 2025
-
1 1 7 As A Fraction
Sep 17, 2025
-
13 As A Fraction Simplified
Sep 17, 2025
-
Lcm Of 18 And 20
Sep 17, 2025
-
Convert 250 Pounds To Kilos
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 1 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.