3 2 3x 9x 4
saludintensiva
Sep 22, 2025 · 5 min read
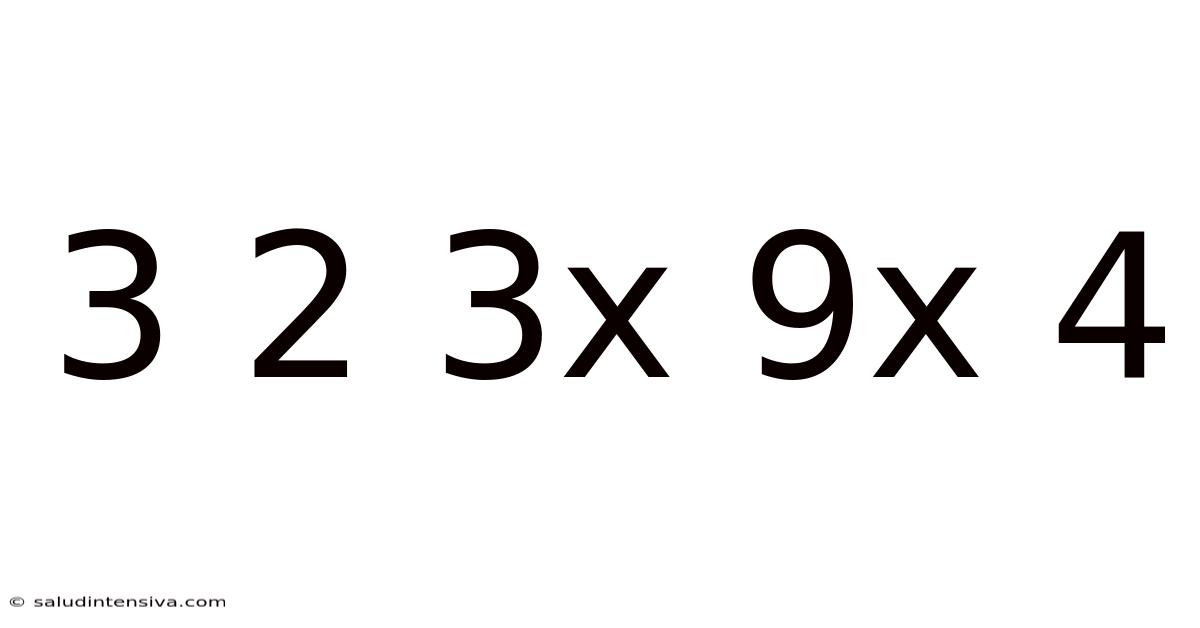
Table of Contents
Decoding the Mystery: Unveiling the Patterns and Possibilities within "3 2 3x 9x 4"
This seemingly simple sequence of numbers, "3 2 3x 9x 4," presents a fascinating puzzle. At first glance, it appears random. However, a deeper dive reveals a multitude of potential interpretations, depending on the lens through which we view it. This article will explore various mathematical and logical approaches to understand this sequence, uncovering hidden patterns and demonstrating the richness of mathematical thinking. We will examine different possibilities, ranging from simple arithmetic operations to more complex algebraic concepts, and even touch upon the intriguing world of combinatorics and probability.
Understanding the Notation: The Significance of "x"
Before we delve into interpretations, let's clarify the meaning of "x" within the sequence. In mathematics, "x" commonly represents a variable or an unknown quantity. In this context, it's crucial to consider whether "x" signifies multiplication or something else entirely. We'll explore both interpretations, exploring the implications of each.
Interpretation 1: Assuming "x" Represents Multiplication
If we interpret "x" as the multiplication operator, the sequence becomes: 3, 2, 3 multiplied by 9 multiplied by 4. This is a straightforward arithmetic problem. Let's break it down:
- Step 1: Multiplication is performed from left to right. First, 3 multiplied by 9 equals 27.
- Step 2: Then, 27 is multiplied by 4, resulting in 108.
Therefore, under this interpretation, the sequence resolves to the single number 108.
Interpretation 2: Exploring Potential Relationships Between the Numbers
If we move beyond the straightforward interpretation of multiplication, we can explore the potential relationships between the numbers themselves. This involves considering different mathematical operations and seeking patterns or underlying rules. For example:
- Differences: Let's calculate the differences between consecutive numbers:
- 2 - 3 = -1
- 3 - 2 = 1
- 9 - 3 = 6
- 4 - 9 = -5
This difference sequence (-1, 1, 6, -5) doesn't immediately reveal a clear pattern.
- Ratios: Let's examine the ratios:
- 2/3 ≈ 0.67
- 3/2 = 1.5
- 9/3 = 3
- 4/9 ≈ 0.44
Again, no immediately apparent pattern emerges from these ratios.
- Sequences within Sequences: Could there be embedded sequences? This approach requires more creativity and a willingness to explore unconventional patterns. For example, we could consider the sequence of odd numbers (3, 9) and the sequence of even numbers (2, 4). But the connection, if any, remains elusive.
Interpretation 3: Introducing Algebra and Equations
Let's introduce algebraic thinking. We can treat "x" as an unknown variable and attempt to construct equations based on the given sequence. Several possibilities exist, depending on our assumptions:
-
Equation 1 (Simple Linear Equation): If we assume a simple linear relationship between consecutive numbers, we might try to solve for "x" using a linear equation. However, without further information or constraints, creating a meaningful equation is challenging. We'd need additional data points or clues about the nature of the relationship.
-
Equation 2 (More Complex Relationships): We could consider more complex relationships, such as quadratic equations or even systems of equations. However, the limited number of data points makes deriving a unique solution incredibly difficult. In this case, multiple equations could fit the data, highlighting the need for more information.
Interpretation 4: Exploring Combinatorics and Probability
If we consider the numbers as individual elements, we can venture into the realm of combinatorics and probability. We could ask questions like:
-
Permutations: How many different arrangements are possible using the numbers 3, 2, 3, 9, and 4? This involves calculating permutations with repetitions, a fundamental concept in combinatorics. The formula for permutations with repetitions is complex and beyond the scope of a concise explanation here.
-
Probability: If we randomly select a number from the sequence, what is the probability of selecting a 3? The probability would be 2/5, since there are two 3s out of a total of five numbers. Similarly, we could calculate the probability of selecting any other number in the sequence.
Interpretation 5: Considering a Coded Message
Perhaps the sequence isn't meant to be solved mathematically in a traditional sense. It could be a code or a cipher. This interpretation opens up a realm of possibilities:
-
Substitution Cipher: Could each number represent a letter of the alphabet? This is a simplistic substitution cipher. However, with only five numbers and 26 letters, this approach would be highly ambiguous and unlikely to produce a meaningful message.
-
More Complex Ciphers: More complex ciphers could involve multiple substitution keys or more intricate encoding schemes. Without a key or further context, deciphering this potential code remains a significant challenge.
Frequently Asked Questions (FAQ)
Q1: Is there a single, definitive solution to the sequence "3 2 3x 9x 4"?
A1: No, there isn't a single definitive solution. The interpretation depends heavily on the assumptions made about the meaning of "x" and the underlying relationships between the numbers.
Q2: What mathematical concepts are relevant to analyzing this sequence?
A2: Several concepts are relevant, including arithmetic operations (addition, subtraction, multiplication, division), algebraic equations, sequences and series, combinatorics, probability, and cryptography (if interpreting it as a code).
Q3: How can I improve my skills in solving similar mathematical puzzles?
A3: Practice is key. Solve various mathematical puzzles and problems regularly. Focus on understanding fundamental mathematical principles and explore different approaches to problem-solving. Look for patterns, try different operations, and don't be afraid to experiment.
Q4: Can this sequence be used to illustrate different mathematical principles in education?
A4: Absolutely. This sequence offers a valuable opportunity to introduce students to multiple mathematical concepts, encouraging critical thinking, problem-solving skills, and the exploration of different solution approaches.
Conclusion: The Value of Open-Ended Mathematical Exploration
The seemingly simple sequence "3 2 3x 9x 4" demonstrates the richness and complexity inherent in even the most basic mathematical problems. There's no single "correct" answer; instead, the sequence invites exploration and the application of diverse mathematical concepts. This ambiguity highlights the importance of creative thinking, pattern recognition, and a willingness to consider multiple perspectives when approaching mathematical puzzles. The exploration undertaken here serves as a reminder that mathematics is not just about finding answers but also about the process of discovery and the development of problem-solving skills. The journey of investigation, often as rewarding as the destination, is what truly makes mathematics fascinating. The value of this exercise lies not just in finding a solution (if one exists), but in the various methodologies employed and the broader understanding gained about mathematical thinking.
Latest Posts
Latest Posts
-
Multiplication Of Decimals Word Problems
Sep 22, 2025
-
115 Degrees F To C
Sep 22, 2025
-
What Is 2200 In Time
Sep 22, 2025
-
Mixed Fraction On Number Line
Sep 22, 2025
-
30 Days From February 28
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 2 3x 9x 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.