3/2 As A Whole Number
saludintensiva
Sep 11, 2025 · 6 min read
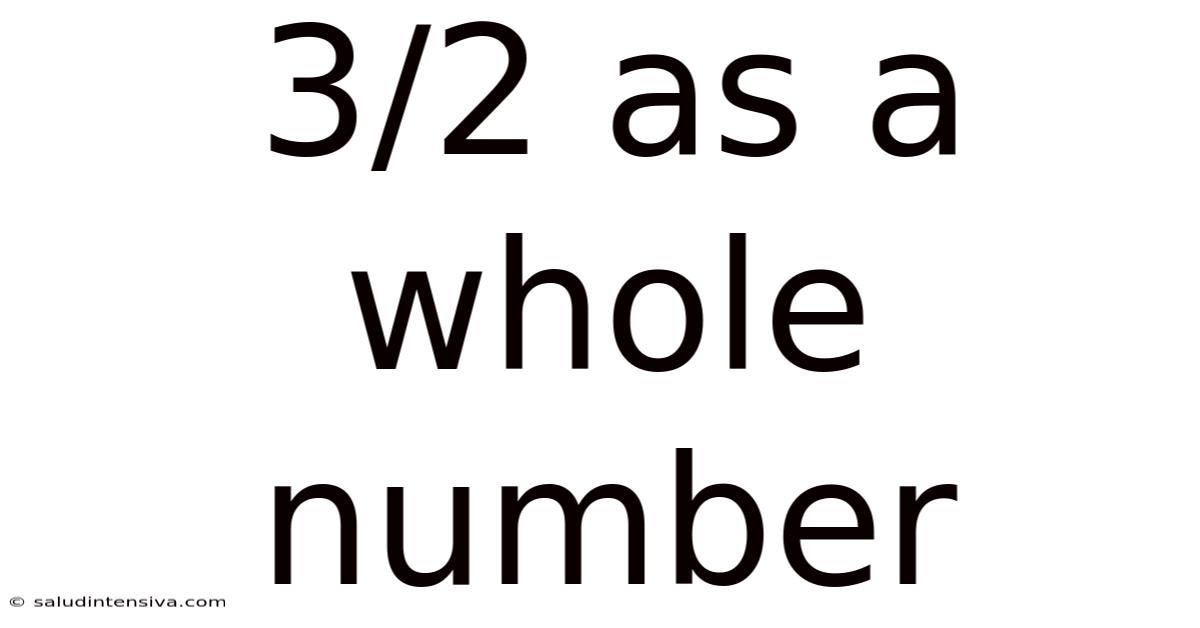
Table of Contents
Understanding 3/2 as a Whole Number: A Deep Dive into Fractions and Mixed Numbers
The question of how 3/2 can be represented as a whole number might seem deceptively simple at first glance. After all, whole numbers are, by definition, integers without fractional parts. However, understanding the intricacies of this seemingly straightforward concept opens the door to a deeper understanding of fractions, mixed numbers, and their relationship to the broader world of mathematics. This article will explore the concept in detail, explaining not only the mechanics of converting 3/2 but also the underlying mathematical principles involved. We will delve into different methods, address common misconceptions, and explore relevant applications.
Introduction: Fractions and Their Components
Before diving into the specifics of 3/2, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It is composed of two key parts:
- Numerator: The top number in a fraction, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
Therefore, in the fraction 3/2, the numerator (3) signifies that we possess three parts, while the denominator (2) signifies that the whole is divided into two equal parts. This immediately tells us that we have more than one whole unit.
Converting 3/2 to a Mixed Number
Since 3/2 represents more than one whole, it's not a whole number in its current form. Instead, it's an improper fraction – a fraction where the numerator is greater than or equal to the denominator. To represent 3/2 as a whole number plus a remaining fraction, we convert it to a mixed number. This process involves division:
-
Divide the numerator by the denominator: 3 ÷ 2 = 1 with a remainder of 1.
-
The quotient becomes the whole number part: The quotient (1) becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fractional part: The remainder (1) becomes the numerator of the fraction.
-
The denominator remains the same: The denominator (2) stays the same.
Therefore, 3/2 is equivalent to the mixed number 1 1/2. This representation clearly shows that we have one whole unit and one-half of another.
Converting 3/2 to a Decimal
Another way to represent 3/2 is as a decimal. This involves the same division process as converting to a mixed number:
- Divide the numerator by the denominator: 3 ÷ 2 = 1.5
Therefore, 3/2 is equivalent to 1.5 as a decimal. This representation is often useful in practical applications and calculations.
Visual Representation of 3/2
Visualizing 3/2 can further solidify our understanding. Imagine a pizza cut into two equal slices. The fraction 3/2 represents having three of these slices. This means we have one whole pizza (two slices) and one extra slice, representing 1 1/2 pizzas. This visual approach can be particularly helpful for beginners grasping the concept of improper fractions.
Why 3/2 Isn't Directly a Whole Number
It's crucial to emphasize that 3/2 itself is not a whole number. Whole numbers are integers (0, 1, 2, 3, and so on) that represent complete units without any fractional parts. While we can express the value of 3/2 using a whole number (1) and a fractional component (1/2), the fraction 3/2 itself contains a fractional part and therefore doesn't fit the definition of a whole number.
Mathematical Operations with 3/2
Understanding the different representations of 3/2 is crucial for performing mathematical operations. For example, let's consider addition:
-
Adding 3/2 to a whole number: If we add 3/2 (or 1.5) to 5, the result is 6.5 or 6 1/2.
-
Adding 3/2 to another fraction: Adding 3/2 to 1/2 results in 4/2, which simplifies to 2 (a whole number).
-
Multiplying or dividing 3/2: Multiplying 3/2 by 2 results in 3. Dividing 3/2 by 1/2 results in 3.
These examples demonstrate how understanding the different representations of 3/2 facilitates accurate calculations.
Common Misconceptions about 3/2
Several common misconceptions surround the representation of 3/2:
-
Rounding: Some might mistakenly round 1.5 to 2. However, rounding changes the precise value. While it might be acceptable in certain contexts (like estimation), it’s crucial to remember that 3/2 is not equal to 2.
-
Ignoring the fractional part: Simply stating that 3/2 is "around 1" is an oversimplification. The fractional part (1/2) is a significant component of the value.
-
Confusing mixed numbers and improper fractions: While 1 1/2 and 3/2 are equivalent, they are different representations. Knowing when to use each is important in different mathematical contexts.
Applications of 3/2 in Real-World Scenarios
The concept of 3/2 finds applications in various real-world scenarios:
-
Measurement: If a recipe calls for 1 1/2 cups of flour, we are working with the equivalent of 3/2 cups.
-
Construction: Measurements in construction often involve fractions, with 3/2 representing a specific length or dimension.
-
Finance: Calculating interest rates or proportions might involve fractional values like 3/2.
-
Data Analysis: In statistical analysis, data might be presented in fractions, necessitating an understanding of their equivalence to decimals or mixed numbers.
Further Exploration: Extending the Concept
The concept of converting improper fractions to mixed numbers extends to other fractions. For instance:
- 5/3 = 1 2/3
- 7/4 = 1 3/4
- 11/5 = 2 1/5
Understanding the underlying principle of division allows you to convert any improper fraction into its equivalent mixed number.
Frequently Asked Questions (FAQ)
Q: Can 3/2 be expressed as a whole number without any remainder?
A: No. 3/2 contains a fractional component (1/2) and therefore cannot be expressed as a whole number without losing information.
Q: What is the difference between an improper fraction and a mixed number?
A: An improper fraction has a numerator greater than or equal to the denominator (e.g., 3/2). A mixed number has a whole number part and a fractional part (e.g., 1 1/2). They represent the same value but in different forms.
Q: Why is it important to understand the different representations of a fraction?
A: Understanding different representations (improper fraction, mixed number, decimal) is crucial for performing accurate mathematical operations and solving real-world problems.
Q: Are there any other ways to represent 3/2?
A: Yes, 3/2 can also be represented as a percentage (150%).
Conclusion: Mastering Fractions – A Building Block of Mathematics
Understanding the representation of 3/2 as a mixed number (1 1/2) or a decimal (1.5) is a foundational concept in mathematics. While it cannot be represented directly as a whole number, grasping its equivalent forms is crucial for progressing to more advanced mathematical concepts. Mastering fractions, including the ability to convert between different representations, lays the groundwork for success in algebra, calculus, and numerous other mathematical fields. The ability to visualize, manipulate, and understand fractions is a critical skill with far-reaching implications across various disciplines and everyday life. Continue practicing and exploring different fractional representations to build a solid mathematical foundation.
Latest Posts
Latest Posts
-
How Long Is 5 Minutes
Sep 11, 2025
-
Volume Of A Oblique Cone
Sep 11, 2025
-
37 Degree Fahrenheit To Celsius
Sep 11, 2025
-
What Percent Is 6 9
Sep 11, 2025
-
Change Fraction To Whole Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3/2 As A Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.