3 2 Divided By 4
saludintensiva
Sep 20, 2025 · 6 min read
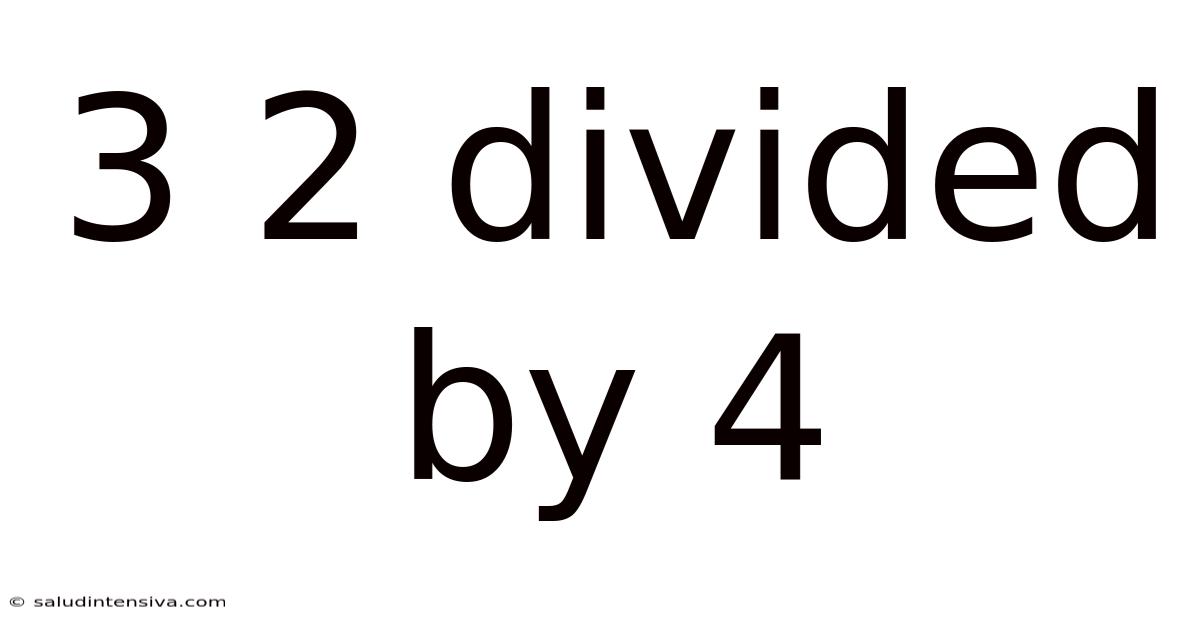
Table of Contents
Decoding 32 Divided by 4: A Deep Dive into Division
This article explores the seemingly simple calculation of 32 divided by 4, delving beyond the basic answer to illuminate the underlying principles of division, its various methods, and its real-world applications. Understanding division is fundamental to mathematics and crucial for various aspects of life, from budgeting to engineering. This comprehensive guide will equip you with a thorough grasp of this essential arithmetic operation.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of "32 divided by 4," we're asking: "How many times does 4 fit into 32?" The answer, as we'll demonstrate in various ways, is 8. But understanding why this is the answer is far more enriching than simply knowing the result. This exploration will cover different approaches to solving this problem, revealing the underlying mathematical concepts.
Method 1: Repeated Subtraction
One of the most intuitive ways to understand division, especially for beginners, is through repeated subtraction. We start with the dividend (32) and repeatedly subtract the divisor (4) until we reach zero. The number of times we subtract is the quotient (the answer).
Let's illustrate:
- 32 - 4 = 28
- 28 - 4 = 24
- 24 - 4 = 20
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
We subtracted 4 a total of eight times. Therefore, 32 divided by 4 equals 8. This method visually demonstrates the concept of division as repeated subtraction, making it easier to grasp the underlying logic.
Method 2: Long Division
Long division is a more formal method for performing division, particularly useful when dealing with larger numbers. While seemingly complex, it's a systematic approach that ensures accuracy. Let's apply it to 32 divided by 4:
8
4 | 32
-32
0
- Divide: How many times does 4 go into 3? It doesn't go in at all, so we move to the next digit. How many times does 4 go into 32? It goes in 8 times (4 x 8 = 32).
- Multiply: Multiply the quotient (8) by the divisor (4): 8 x 4 = 32.
- Subtract: Subtract the result (32) from the dividend (32): 32 - 32 = 0.
- Bring Down: There are no more digits to bring down. The remainder is 0.
The final result is 8. Long division provides a structured approach, making it suitable for more complex division problems.
Method 3: Multiplication as the Inverse of Division
Division and multiplication are inverse operations. This means that if we multiply the quotient (the answer to a division problem) by the divisor, we should get the dividend (the original number being divided). This acts as a check on our answer.
In our example:
- Quotient: 8
- Divisor: 4
- Dividend: 32
8 x 4 = 32. Since this matches our original dividend, we can confirm that 32 divided by 4 is indeed 8. This inverse relationship is a fundamental concept in arithmetic.
Method 4: Visual Representation with Objects
A visual approach, particularly helpful for younger learners, involves using physical objects. Imagine 32 counters. We can group these counters into sets of 4. By counting the number of groups, we find our answer. This provides a concrete representation of the abstract concept of division.
The Significance of Remainders: Beyond Whole Numbers
While 32 divided by 4 results in a whole number (8), many division problems produce remainders. A remainder is the amount left over after dividing as evenly as possible. For example, if we divided 35 by 4:
8 R 3
4 | 35
-32
3
Here, 4 goes into 35 eight times (4 x 8 = 32), leaving a remainder of 3. Understanding remainders is crucial in various contexts, from sharing items equally to more advanced mathematical concepts.
Real-World Applications of Division
Division is far from an abstract mathematical concept; it's an essential tool used daily in countless situations:
- Sharing: Dividing a cake amongst friends, splitting a bill at a restaurant, or distributing candies equally among children.
- Measurement: Converting units (e.g., converting inches to feet), calculating average speed, or determining the number of tiles needed to cover a floor.
- Finance: Budgeting, calculating unit costs, determining profit margins, or dividing assets.
- Engineering: Calculating ratios, determining dimensions, or distributing loads.
- Cooking: Scaling recipes, dividing ingredients proportionally, or calculating serving sizes.
The applications are extensive and demonstrate the practicality and importance of mastering division.
Exploring Fractions: Connecting Division to Fractions
The division problem "32 divided by 4" can also be represented as a fraction: 32/4. This fraction represents 32 parts out of a total of 4 equal parts. Simplifying this fraction gives us the answer:
32/4 = 8/1 = 8
This connection highlights the relationship between division and fractions, two fundamental concepts within mathematics.
Expanding the Concept: Division with Decimals and Larger Numbers
While we've focused on whole numbers, division extends to decimals and much larger numbers. The same principles apply, but the calculations may become more complex, often requiring the use of a calculator or more advanced techniques. Mastering the fundamental principles illustrated here provides a strong foundation for tackling these more challenging problems.
Frequently Asked Questions (FAQs)
Q: What is the dividend in the equation 32 divided by 4?
A: The dividend is 32. It's the number being divided.
Q: What is the divisor in the equation 32 divided by 4?
A: The divisor is 4. It's the number by which we are dividing.
Q: What is the quotient in the equation 32 divided by 4?
A: The quotient is 8. It's the result of the division.
Q: What if the dividend is smaller than the divisor?
A: If the dividend is smaller than the divisor, the quotient will be less than 1 (often represented as a decimal or fraction). For example, 3 divided by 4 is 0.75 or 3/4.
Q: How can I practice my division skills?
A: Practice is key! Work through various division problems, starting with simpler examples and gradually increasing the difficulty. Use different methods to reinforce your understanding. You can find numerous online resources and worksheets to help you practice.
Conclusion: Mastering Division—A Building Block for Success
Understanding 32 divided by 4 goes far beyond simply obtaining the answer of 8. This seemingly simple calculation provides a window into the fundamental principles of division, its various methods of calculation, and its extensive real-world applications. By grasping these concepts, you’re not just learning a mathematical operation; you're building a critical foundation for success in mathematics and beyond. From budgeting to engineering, the ability to divide accurately and efficiently is a valuable skill that transcends the classroom and empowers you to tackle numerous challenges in everyday life. Remember, practice makes perfect, so keep exploring and practicing different division problems to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
New Way To Do Multiplication
Sep 20, 2025
-
Square Root Of 5 Simplified
Sep 20, 2025
-
Conversion 9 16 En Mm
Sep 20, 2025
-
Mean Median Mode Range Outlier
Sep 20, 2025
-
40 Out Of 55 Percentage
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 2 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.