3 20 As A Decimal
saludintensiva
Sep 24, 2025 · 5 min read
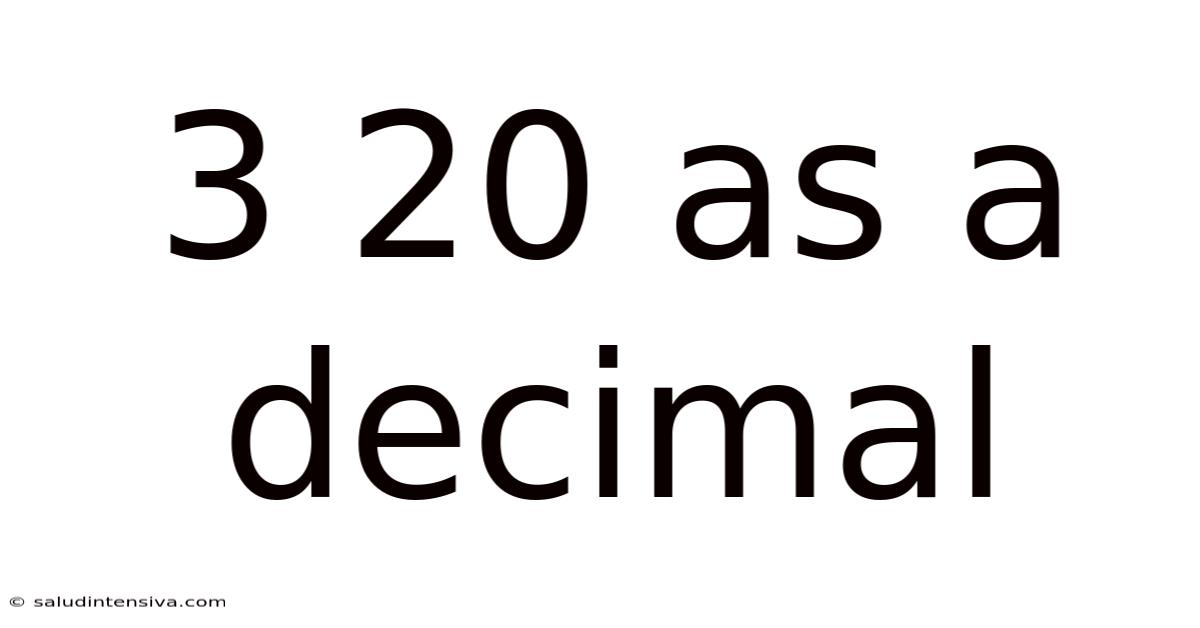
Table of Contents
Understanding 3/20 as a Decimal: A Comprehensive Guide
Many everyday situations require converting fractions to decimals. Whether you're calculating percentages, working with measurements, or solving mathematical problems, knowing how to perform this conversion is a valuable skill. This article provides a comprehensive explanation of how to convert the fraction 3/20 into a decimal, covering various methods and underlying mathematical principles. We will also explore the broader context of fraction-to-decimal conversion and delve into some related concepts.
Introduction to Fraction-to-Decimal Conversion
Fractions and decimals are two different ways to represent the same numerical value. A fraction expresses a part of a whole, while a decimal uses a base-10 system to represent numbers less than one. Converting between fractions and decimals is a fundamental mathematical process. The fraction 3/20 represents three out of twenty equal parts of a whole. Our goal is to express this same value as a decimal number, typically expressed with a point (.) separating the whole number part from the fractional part.
Method 1: Direct Division
The most straightforward method for converting a fraction to a decimal is through direct division. We simply divide the numerator (the top number) by the denominator (the bottom number). In the case of 3/20, we perform the following calculation:
3 ÷ 20 = 0.15
Therefore, 3/20 as a decimal is 0.15. This is a simple and effective method, especially for fractions with relatively small denominators.
Method 2: Converting to an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
Another approach involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). This method simplifies the conversion process because it directly relates to the place value system used in decimals.
To convert 3/20 to an equivalent fraction with a denominator of 100, we need to multiply both the numerator and the denominator by 5:
(3 × 5) / (20 × 5) = 15/100
Since 15/100 represents 15 hundredths, we can easily write this as a decimal: 0.15. This method is particularly useful when the denominator is a factor of a power of 10.
Understanding the Underlying Mathematical Principles
Both methods described above are based on the fundamental principle of equivalent fractions. Multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. This is because you are essentially multiplying or dividing by 1 (e.g., 5/5 = 1). This principle is crucial for understanding why both methods yield the same decimal result.
The direct division method relies on the definition of a fraction as a division problem. The fraction a/b is equivalent to the division a ÷ b. The result of this division will always be a decimal representation of the fraction.
The equivalent fraction method uses the properties of equivalent fractions to manipulate the fraction into a form that directly translates into a decimal. Fractions with denominators that are powers of 10 are easily converted into decimals because their place values are directly related to the decimal system (tenths, hundredths, thousandths, etc.).
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals has wide-ranging practical applications across numerous fields:
-
Finance: Calculating percentages, interest rates, and proportions of investments often involves converting fractions to decimals. For example, a 3/20 discount would be equivalent to a 0.15 or 15% discount.
-
Measurement: Many measurement systems involve both fractional and decimal representations. Converting between these systems ensures accurate calculations and comparisons. For instance, in construction or engineering, understanding the decimal equivalent of a fractional measurement is critical for precision.
-
Science: Scientific data often involves fractional values, which are typically converted to decimals for calculations and analysis. This is particularly crucial in fields like chemistry and physics where precise measurements are essential.
-
Everyday Calculations: From calculating tips in a restaurant to determining the amount of ingredients in a recipe, the ability to convert fractions to decimals simplifies everyday calculations.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions can be converted to either terminating decimals (decimals that end) or repeating decimals (decimals that have a repeating pattern of digits). Fractions that can be expressed with denominators that are only multiples of 2 and/or 5 will always result in terminating decimals. Fractions with other prime factors in the denominator will result in repeating decimals.
Q: What if the decimal representation is a repeating decimal? How do I handle that?
A: Repeating decimals are indicated by placing a bar over the repeating sequence of digits. For example, 1/3 = 0.3333... is written as 0.3̅. While some calculations may require carrying the repeating decimal to a certain level of precision, many calculators and computer programs can handle these types of decimals effectively.
Q: Are there other methods to convert fractions to decimals besides the two mentioned above?
A: While the direct division and equivalent fraction methods are the most common, there are other less frequently used methods involving long division or using specialized calculators. However, for most practical purposes, the two described methods suffice.
Q: What if I have a mixed number (a whole number and a fraction)? How do I convert it to a decimal?
A: Convert the fractional part of the mixed number to a decimal using either method and then add the whole number part. For example, 2 3/20 would be converted to 2 + 0.15 = 2.15
Conclusion
Converting the fraction 3/20 to a decimal is a fundamental skill with wide-ranging applications. Whether you use the direct division method or the equivalent fraction method, understanding the underlying mathematical principles ensures accuracy and enhances your problem-solving abilities. Mastering this skill improves your proficiency in mathematics and allows you to tackle various numerical challenges with greater confidence. The simplicity of the conversion (3/20 = 0.15) belies the importance of understanding the process and its applications across diverse fields. Remember, the ability to switch fluently between fractions and decimals is a valuable tool in your mathematical toolkit.
Latest Posts
Latest Posts
-
90 Days From 8 27
Sep 24, 2025
-
5 Square Root Of 8
Sep 24, 2025
-
Average Speed Of A Plane
Sep 24, 2025
-
18c Is What In Fahrenheit
Sep 24, 2025
-
Inch Conversion Decimal To Fraction
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 3 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.