3.25 Percent As A Decimal
saludintensiva
Sep 12, 2025 · 5 min read
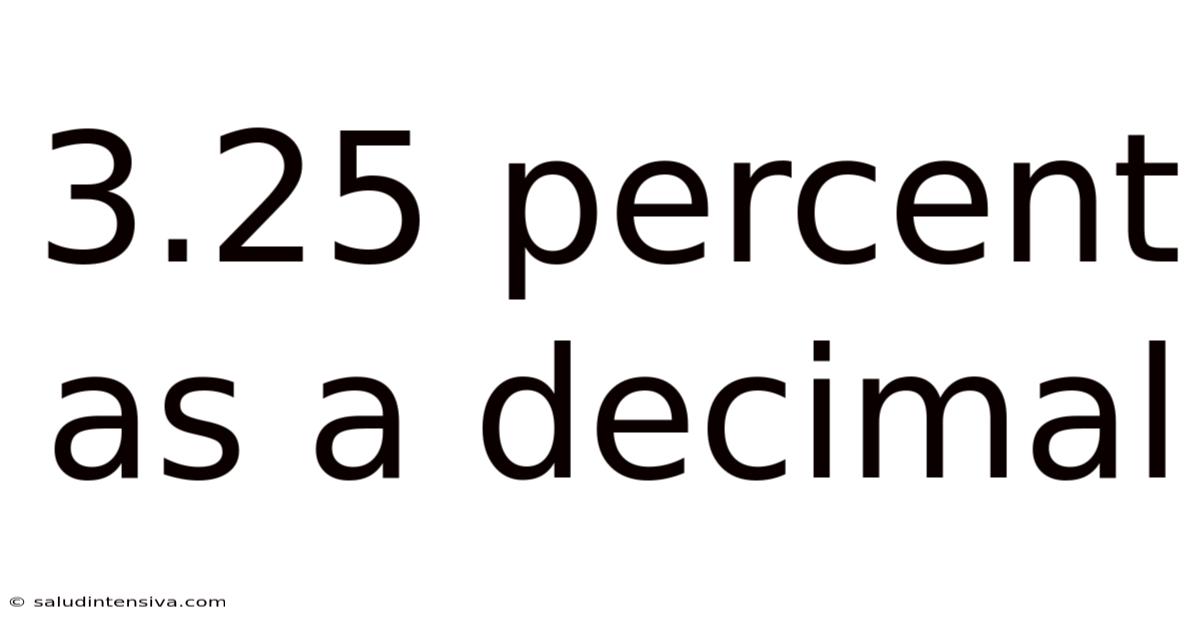
Table of Contents
Understanding 3.25 Percent as a Decimal: A Comprehensive Guide
Converting percentages to decimals is a fundamental skill in mathematics, crucial for various applications from calculating discounts and interest rates to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting 3.25 percent to its decimal equivalent, explaining the underlying principles and providing practical examples. We'll explore different methods, address common misconceptions, and equip you with the knowledge to confidently tackle similar conversions. By the end, you'll not only know the answer but also understand the "why" behind the conversion process.
Introduction: Percentages and Decimals – A Symbiotic Relationship
Percentages and decimals are two different ways of representing the same numerical value. A percentage, denoted by the symbol %, represents a fraction of 100. For instance, 50% means 50 out of 100, or 50/100. A decimal, on the other hand, uses a base-ten system to represent numbers, with a decimal point separating the whole number part from the fractional part. Understanding the relationship between them is key to successful conversion. This article focuses on converting 3.25%, a percentage that includes a decimal component within the percentage itself, highlighting the extra steps required for accurate conversion.
Method 1: The Direct Conversion Method
The most straightforward way to convert a percentage to a decimal is to divide the percentage by 100. This method works regardless of whether the percentage contains a decimal or is a whole number. Let's apply this to 3.25%:
-
Write the percentage as a fraction: 3.25% can be written as 3.25/100.
-
Divide the numerator by the denominator: Performing the division 3.25 ÷ 100 gives us 0.0325.
Therefore, 3.25% as a decimal is 0.0325.
Method 2: Understanding the Place Value Shift
Another way to visualize the conversion involves understanding the place value system. When we divide a number by 100, we essentially move the decimal point two places to the left. Consider the number 3.25.
-
3.25: This is our starting number.
-
03.25: Adding a zero to the left doesn't change the value. This helps visualize the shift.
-
0.325: Moving the decimal point two places to the left effectively divides the number by 100, converting the number into its decimal equivalent.
This method is especially helpful for mental calculations and reinforces the understanding behind the division process.
Method 3: Converting to a Fraction First (for deeper understanding)
For a more thorough understanding, we can convert the percentage to a fraction before converting to a decimal.
-
Rewrite the percentage as a fraction: 3.25% means 3.25 out of 100, or 3.25/100.
-
Remove the decimal from the numerator: To remove the decimal in the numerator, we multiply both the numerator and the denominator by 100 (since there are two digits after the decimal point). This gives us (3.25 x 100) / (100 x 100) = 325/10000.
-
Simplify the fraction (if possible): In this case, we can simplify by dividing both the numerator and the denominator by 25, resulting in 13/400.
-
Convert the simplified fraction to a decimal: Now, perform the division 13 ÷ 400, which results in 0.0325.
This method might seem longer, but it emphasizes the connection between percentages, fractions, and decimals, providing a strong foundation for understanding the underlying mathematical concepts.
Practical Applications of 3.25% as a Decimal (0.0325)
The decimal equivalent of 3.25%, which is 0.0325, finds numerous applications in various fields:
-
Finance: Calculating interest on loans or investments. If you have a savings account with a 3.25% annual interest rate, you would use 0.0325 to calculate the interest earned.
-
Sales and Discounts: Determining the discount amount on sale items. A 3.25% discount on a $100 item would be calculated as $100 x 0.0325 = $3.25.
-
Statistics: Representing proportions or probabilities. If 3.25% of a population has a certain characteristic, this can be expressed as 0.0325 in statistical analysis.
-
Taxes: Calculating tax amounts. A 3.25% sales tax on a purchase would be computed using the decimal equivalent.
-
Real Estate: Calculating property tax rates. A property tax rate of 3.25% is more easily used in calculations when represented as 0.0325.
Addressing Common Misconceptions
One common mistake is to simply move the decimal point two places to the left without considering the percentage symbol. Remember, the percentage symbol signifies "out of 100," and the division by 100 is an essential step in the conversion. Simply moving the decimal point in a number without dividing by 100 will result in an incorrect value.
Explanation of the Scientific Basis
The conversion from percentage to decimal rests on the fundamental definition of a percentage as a fraction of 100. The mathematical operation of dividing by 100 is a direct consequence of this definition. The process aligns with the principles of fractional arithmetic and the decimal number system. The movement of the decimal point two places to the left is merely a shortcut derived from the division by 100. It's essential to understand that this shortcut is based on the underlying mathematical principle of dividing the percentage value by 100.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to convert percentages to decimals?
-
A: Absolutely! Calculators make the conversion very easy. Simply enter the percentage value and divide it by 100.
-
Q: What if the percentage is a whole number (e.g., 5%)?
-
A: The same principle applies. Divide the whole number by 100 (e.g., 5% = 5/100 = 0.05).
-
Q: What if the percentage has more than two decimal places (e.g., 3.255%)?
-
A: The process remains the same. Divide the number by 100. 3.255% = 3.255/100 = 0.03255.
-
Q: Why is understanding this conversion important?
-
A: This conversion is fundamental for applying mathematical concepts in various real-world situations, from personal finance to scientific calculations. It provides a crucial link between percentages, fractions, and decimals, strengthening your overall mathematical understanding.
Conclusion: Mastering Percentage-to-Decimal Conversions
Converting 3.25% to its decimal equivalent, 0.0325, is a simple yet essential mathematical skill with broad applicability. Understanding the underlying principles – the definition of a percentage as a fraction of 100 and the subsequent division – allows you to confidently handle various percentage-to-decimal conversions. This knowledge is invaluable in numerous fields, empowering you to tackle calculations involving discounts, interest rates, statistics, and many other applications with accuracy and efficiency. Remember the three methods presented – the direct method, the place value shift, and the fraction-based method – to reinforce your understanding and choose the approach that best suits your learning style. Practice these conversions regularly to solidify your skills and build a strong foundation in mathematical concepts.
Latest Posts
Latest Posts
-
3 4 5 Improper Fraction
Sep 12, 2025
-
What Is Half Of 55
Sep 12, 2025
-
16 5 As A Decimal
Sep 12, 2025
-
Convert 87 Fahrenheit To Celsius
Sep 12, 2025
-
What Is 15 Of 45
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3.25 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.