3 3/10 As A Decimal
saludintensiva
Sep 19, 2025 · 5 min read
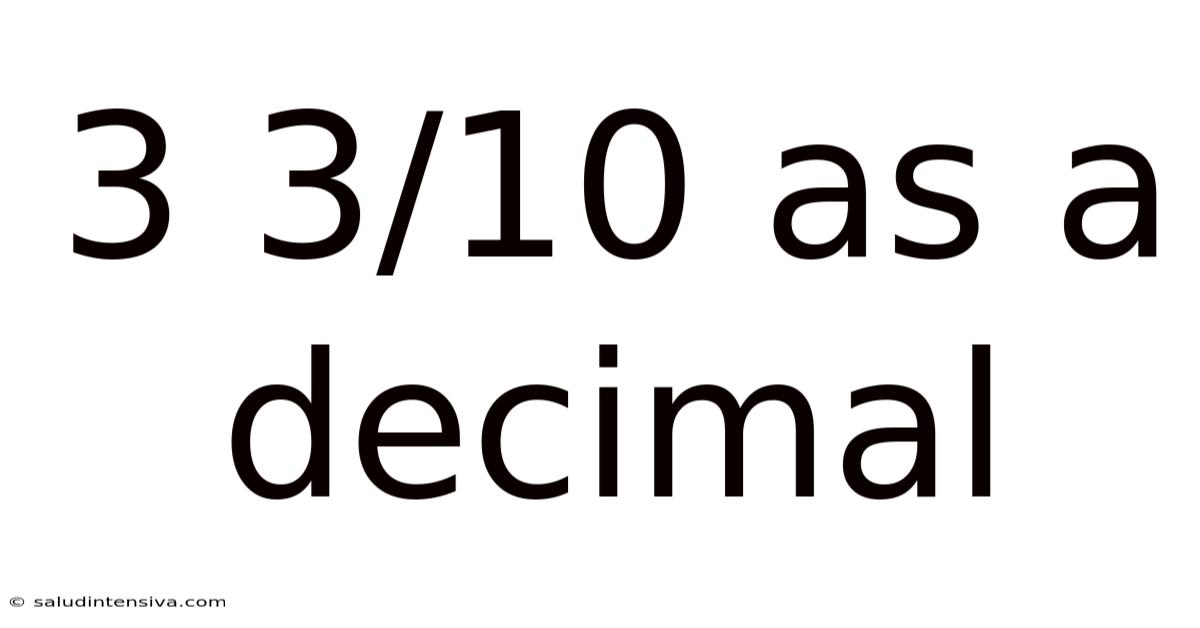
Table of Contents
3 3/10 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the mixed number 3 3/10 into its decimal equivalent, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also address common questions and misconceptions surrounding decimal representation. This guide is designed for learners of all levels, from those just beginning to grasp fractions to those seeking a deeper understanding of numerical representation.
Introduction: Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's clarify the terms involved. A mixed number combines a whole number and a fraction, such as 3 3/10. This represents three whole units and three-tenths of another unit. A decimal, on the other hand, uses a base-ten system to represent numbers, using a decimal point to separate the whole number part from the fractional part. For instance, 3.3 is a decimal number representing three and three-tenths. Our goal is to express the mixed number 3 3/10 in this decimal format.
Step-by-Step Conversion of 3 3/10 to Decimal
The conversion process is straightforward and involves two main steps:
1. Convert the Fraction to a Decimal:
The core of the conversion lies in transforming the fraction 3/10 into its decimal equivalent. Remember that the denominator of a fraction represents the number of equal parts a whole is divided into, while the numerator represents how many of those parts we have. In 3/10, the whole is divided into 10 equal parts, and we have 3 of them.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
3 ÷ 10 = 0.3
This tells us that 3/10 is equal to 0.3.
2. Combine the Whole Number and the Decimal:
Now that we've converted the fractional part, we combine it with the whole number part of the mixed number. In 3 3/10, the whole number is 3. Therefore, the decimal equivalent of 3 3/10 is:
3 + 0.3 = 3.3
Therefore, 3 3/10 as a decimal is 3.3.
Understanding the Place Value System
The decimal system is based on powers of 10. Each place value to the right of the decimal point represents a decreasing power of 10. The first place after the decimal point represents tenths (1/10), the second place represents hundredths (1/100), the third place represents thousandths (1/1000), and so on. In 3.3, the '3' after the decimal point occupies the tenths place, signifying three-tenths.
Alternative Method: Converting to an Improper Fraction First
While the above method is the most straightforward, an alternative approach involves first converting the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
1. Convert to an Improper Fraction:
To convert 3 3/10 to an improper fraction, we multiply the whole number (3) by the denominator (10) and add the numerator (3):
(3 × 10) + 3 = 33
This becomes the new numerator, while the denominator remains the same:
33/10
2. Divide the Numerator by the Denominator:
Now, divide the numerator (33) by the denominator (10):
33 ÷ 10 = 3.3
This yields the same decimal result as the previous method.
Why Understanding Decimal Conversions is Important
The ability to convert between fractions and decimals is crucial for several reasons:
- Real-world Applications: Many real-world measurements and calculations involve decimals. For instance, currency, weights, and measurements are often expressed using decimals.
- Problem Solving: Converting fractions to decimals simplifies many mathematical problems, especially those involving calculations with mixed numbers.
- Data Analysis: In statistics and data analysis, decimal representation is commonly used for representing proportions and probabilities.
- Scientific Calculations: Decimal representation is essential in scientific calculations and measurements.
Common Misconceptions and Troubleshooting
Several common misconceptions can hinder the understanding of decimal conversion:
- Confusion with Whole Numbers: Students might mistakenly think that 3 3/10 is simply 33. Remember that the mixed number indicates a whole number and a fraction.
- Incorrect Placement of the Decimal Point: Ensure the decimal point is correctly positioned after the whole number and before the decimal representation of the fraction.
- Difficulty with Division: Difficulties in performing division, especially with larger numbers, can lead to errors. Practice division skills to enhance accuracy.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be easily converted to terminating decimals?
No, not all fractions can be easily converted to terminating decimals. Fractions with denominators that are not multiples of 2 or 5 (or a combination thereof) will result in recurring or repeating decimals. For example, 1/3 = 0.3333...
Q2: What if the fraction has a larger numerator than denominator?
If the fraction has a larger numerator than denominator (an improper fraction), the decimal representation will have a whole number part greater than 0.
Q3: How do I convert decimals back to fractions?
To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (10, 100, 1000, etc.), depending on the number of digits after the decimal point. Then, simplify the fraction to its lowest terms.
Q4: What about more complex mixed numbers?
The principles remain the same for more complex mixed numbers. Convert the fractional part to a decimal by dividing the numerator by the denominator and then add the whole number part.
Conclusion: Mastering Decimal Conversions
Converting 3 3/10 to its decimal equivalent, 3.3, is a relatively simple process involving the division of the fraction's numerator by its denominator and the addition of the whole number part. However, understanding the underlying principles of the decimal system and place value is crucial for applying this skill to a wider range of mathematical problems. By mastering decimal conversions, you open doors to a deeper understanding of numbers and their representations, equipping you with a valuable skill for various mathematical and real-world applications. Remember to practice regularly to build confidence and proficiency. Consistent practice will solidify your understanding and help you confidently navigate the world of fractions and decimals.
Latest Posts
Latest Posts
-
5 8 As A Mixed Number
Sep 19, 2025
-
20 Percent Out Of 30
Sep 19, 2025
-
2 To The Power 6
Sep 19, 2025
-
Greatest Common Factor Of 60
Sep 19, 2025
-
3 4 Of 4 5
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 3/10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.