3 4 As A Percent
saludintensiva
Sep 11, 2025 · 5 min read
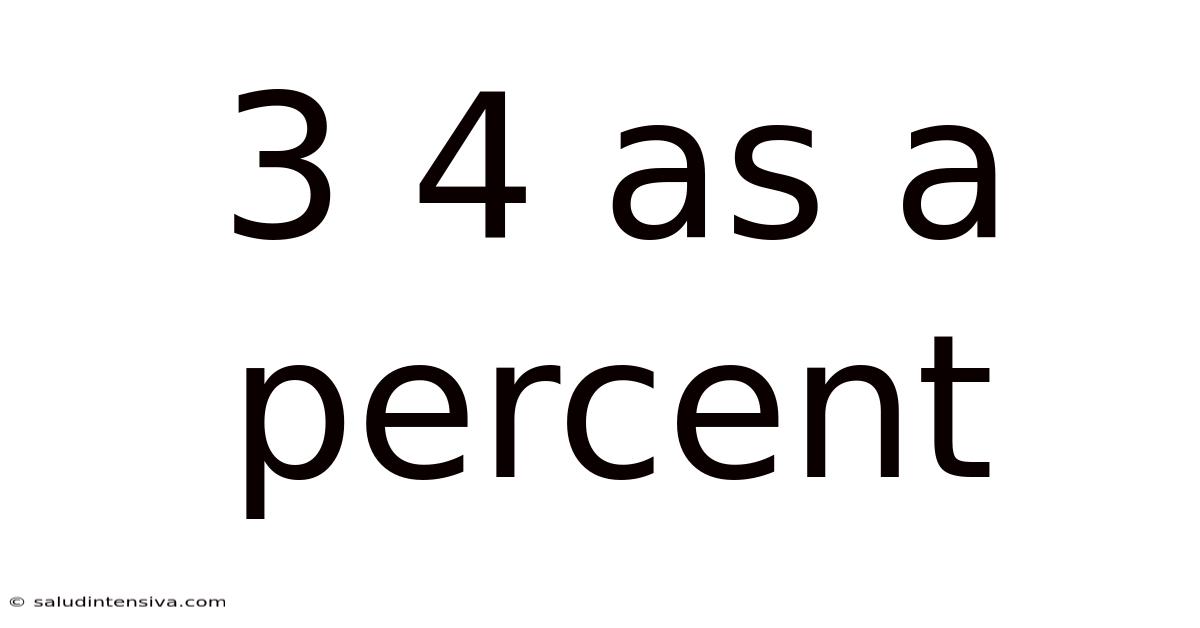
Table of Contents
Understanding 3/4 as a Percent: A Comprehensive Guide
Fractions, decimals, and percentages are fundamental concepts in mathematics, crucial for everyday life and various professional fields. This comprehensive guide delves into the conversion of the fraction 3/4 into its percentage equivalent, exploring the underlying principles and providing practical applications. Understanding this conversion is key to mastering basic arithmetic and applying it to real-world scenarios, such as calculating discounts, understanding statistics, and more. We'll break down the process step-by-step, ensuring clarity for learners of all levels.
Introduction: Fractions, Decimals, and Percentages - A Unified System
Before diving into the specifics of converting 3/4 to a percentage, let's establish the relationship between fractions, decimals, and percentages. They are simply different ways of representing the same value – a part of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For instance, 3/4 represents three parts out of four equal parts.
-
Decimals: Represent a part of a whole using a base-ten system, utilizing a decimal point to separate whole numbers from fractional parts. For example, 0.75 represents seventy-five hundredths.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" signifies "per cent" or "out of 100". For instance, 75% represents 75 parts out of 100 equal parts.
All three systems are interchangeable, meaning you can convert one form into another without changing the underlying value. This interoperability is essential for problem-solving in various contexts.
Method 1: Converting 3/4 to a Decimal, then to a Percentage
This method involves a two-step process: first converting the fraction to a decimal and then the decimal to a percentage.
Step 1: Converting the Fraction to a Decimal
To convert a fraction to a decimal, simply divide the numerator by the denominator. In this case:
3 ÷ 4 = 0.75
Therefore, 3/4 is equivalent to 0.75.
Step 2: Converting the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
0.75 x 100 = 75
Therefore, 0.75 is equivalent to 75%.
Conclusion of Method 1: Following these steps, we definitively establish that 3/4 is equal to 75%.
Method 2: The Direct Percentage Conversion Method
This method involves a more direct approach, leveraging the understanding that percentages are inherently fractions with a denominator of 100.
To convert 3/4 to a percentage directly, we need to find an equivalent fraction with a denominator of 100. We can achieve this by finding a number that, when multiplied by 4, results in 100.
100 ÷ 4 = 25
Now, multiply both the numerator and denominator of 3/4 by 25:
(3 x 25) / (4 x 25) = 75/100
Since 75/100 represents 75 parts out of 100, this directly translates to 75%.
Method 3: Using Proportions to Find the Percentage
This method utilizes the concept of proportions to solve for the percentage equivalent. We can set up a proportion where one ratio represents the fraction 3/4 and the other represents the unknown percentage (x) over 100.
3/4 = x/100
To solve for x, we cross-multiply:
4x = 300
Now, divide both sides by 4:
x = 75
Therefore, 3/4 is equal to 75%.
The Scientific Explanation: Ratio and Proportion
The conversion from fractions to percentages fundamentally relies on the mathematical concepts of ratio and proportion. A ratio compares two quantities, while a proportion states that two ratios are equal. When we convert 3/4 to a percentage, we are essentially establishing a proportion between the fraction and its equivalent representation out of 100.
The fraction 3/4 represents a ratio of 3 to 4. To express this ratio as a percentage, we need to find an equivalent ratio where the second term (the denominator) is 100. This is achieved through the methods outlined earlier – either by direct multiplication or by solving a proportion. The resulting ratio (75/100) directly translates to 75%. This underlying principle of ratio and proportion solidifies the mathematical foundation of percentage calculations.
Practical Applications of 3/4 (75%)
The knowledge that 3/4 equals 75% has wide-ranging practical applications in many areas of life:
-
Calculating Discounts: A 75% discount on a $100 item means you save $75 (75% of $100).
-
Understanding Statistics: If 3 out of 4 people prefer a particular product, this represents a 75% preference rate.
-
Measuring Progress: Completing 3 out of 4 tasks translates to 75% completion.
-
Baking and Cooking: Many recipes use fractions, and understanding their percentage equivalents can help with scaling recipes up or down.
-
Financial Calculations: Interest rates, tax calculations, and other financial computations often involve percentages, making this conversion essential.
Frequently Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
A1: Yes, absolutely! Any fraction can be converted to a percentage by following the methods described above. Simply divide the numerator by the denominator to obtain the decimal equivalent and then multiply by 100 to get the percentage.
Q2: What if the decimal has many digits after the decimal point?
A2: If the decimal has many digits, you can round it to a reasonable number of decimal places depending on the context of the problem. For instance, you might round to two decimal places for most everyday applications.
Q3: Are there other fractions that easily convert to whole number percentages?
A3: Yes, many fractions have simple percentage equivalents. For example: 1/2 = 50%, 1/4 = 25%, 1/5 = 20%, 1/10 = 10%, etc. These are commonly used and useful to memorize.
Q4: Why is understanding percentages important?
A4: Percentages are a crucial tool for communication and understanding data in various contexts. They provide a standardized and easily understandable way to represent proportions and comparisons, making them essential for various applications, from everyday shopping to complex financial analysis.
Conclusion: Mastering the Conversion of 3/4 to 75%
Understanding the conversion of 3/4 to 75% is not just about rote memorization; it's about grasping the underlying principles of fractions, decimals, and percentages. By understanding the methods presented here – direct conversion, decimal conversion, and proportional methods – you'll be able to confidently tackle similar conversions and apply them to real-world problems. This knowledge empowers you to interpret data, make calculations, and ultimately, become more proficient in mathematical applications across various fields. Remember, consistent practice is key to mastering these concepts and building confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Pound To Troy Ounce Conversion
Sep 11, 2025
-
1 2 Acre Sq Ft
Sep 11, 2025
-
1 2 4 In Fraction
Sep 11, 2025
-
Gcf For 6 And 9
Sep 11, 2025
-
Gcf Of 15 And 60
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.