3 4 Divided 1 6
saludintensiva
Sep 22, 2025 · 6 min read
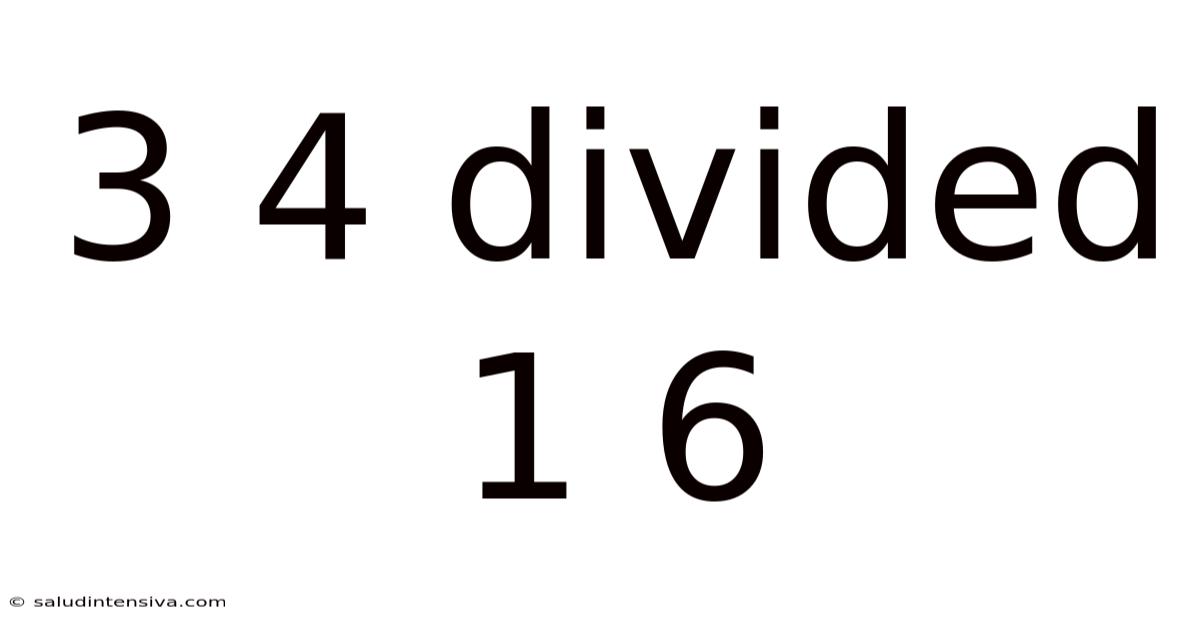
Table of Contents
Decoding 3/4 Divided by 1/6: A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting at first, but with a clear, step-by-step approach, it becomes manageable and even enjoyable. This comprehensive guide will break down the process of dividing 3/4 by 1/6, explaining the underlying principles and offering multiple methods to solve this type of problem. We'll explore the concept of reciprocal, the visual representation of division, and address frequently asked questions, ensuring a complete understanding of this fundamental mathematical operation.
Introduction: Why Fraction Division Matters
Fraction division is a crucial skill in mathematics, applicable in various fields, from cooking and sewing to engineering and finance. Mastering this skill allows you to solve real-world problems involving ratios, proportions, and the division of quantities. The seemingly simple problem of 3/4 divided by 1/6, while seemingly straightforward, provides a perfect illustration of the core concepts and techniques involved in fraction division. Understanding this example unlocks the ability to tackle more complex fraction problems with confidence. This guide will equip you with the knowledge and tools to confidently solve similar problems and build a strong foundation in arithmetic.
Method 1: The Reciprocal Method - The Most Common Approach
The most common and efficient method for dividing fractions involves using the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/6 is 6/1 (or simply 6). The process for dividing fractions is as follows:
-
Identify the dividend and the divisor: In the problem 3/4 divided by 1/6, 3/4 is the dividend (the number being divided), and 1/6 is the divisor (the number you're dividing by).
-
Find the reciprocal of the divisor: The reciprocal of 1/6 is 6/1.
-
Change the division to multiplication: Instead of dividing by 1/6, we multiply by its reciprocal, 6/1. Our problem now becomes: 3/4 * 6/1.
-
Multiply the numerators and the denominators: Multiply the numerators (top numbers) together: 3 * 6 = 18. Then, multiply the denominators (bottom numbers) together: 4 * 1 = 4. This gives us the fraction 18/4.
-
Simplify the fraction: The fraction 18/4 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2. 18 divided by 2 is 9, and 4 divided by 2 is 2. Therefore, the simplified answer is 9/2.
-
Convert to a mixed number (optional): While 9/2 is a perfectly acceptable answer, it can also be expressed as a mixed number. To do this, divide the numerator (9) by the denominator (2). 9 divided by 2 is 4 with a remainder of 1. This means 9/2 is equal to 4 1/2.
Therefore, 3/4 divided by 1/6 = 9/2 or 4 1/2.
Method 2: Visual Representation - Understanding the Concept
Visualizing the division of fractions can provide a deeper understanding of the process. Let's imagine a pizza cut into four equal slices. We have 3/4 of the pizza (3 slices). Now we want to divide these 3 slices into portions of 1/6 of a pizza. How many portions of 1/6 can we get from 3/4?
This visual representation is difficult to solve directly. Instead, we can find a common denominator. The common denominator for 4 and 6 is 12. Converting 3/4 and 1/6 to twelfths, we get 9/12 and 2/12 respectively. Now we're asking how many times 2/12 goes into 9/12. This is equivalent to 9/12 divided by 2/12 which simplifies to 9/2 (or 4 1/2). This visual method reinforces the reciprocal method, showing that dividing by a fraction is the same as multiplying by its reciprocal.
Method 3: Common Denominator Method - A More Intuitive Approach (For Beginners)
While the reciprocal method is generally faster, using a common denominator can be more intuitive for beginners.
-
Find a common denominator: Find the least common multiple of the denominators 4 and 6. This is 12.
-
Convert fractions to equivalent fractions with the common denominator:
- 3/4 becomes 9/12 (multiply numerator and denominator by 3).
- 1/6 becomes 2/12 (multiply numerator and denominator by 2).
-
Divide the numerators: Divide the numerator of the first fraction (9) by the numerator of the second fraction (2): 9 ÷ 2 = 4.5 or 9/2.
-
Keep the common denominator: The denominator remains 12.
This process, while appearing different, ultimately gives the same result: 9/2 or 4 1/2, but it emphasizes the idea of dividing parts of a whole.
The Mathematical Explanation Behind the Reciprocal Method
The reciprocal method isn't just a trick; it's rooted in the fundamental principles of division and fractions. Dividing by a fraction is equivalent to multiplying by its multiplicative inverse (reciprocal). This stems from the definition of division: a ÷ b is the number that, when multiplied by b, gives a. When we multiply 3/4 by the reciprocal of 1/6 (which is 6/1), we are effectively finding the number that, when multiplied by 1/6, equals 3/4. This ultimately leads to the same solution obtained through the other methods.
Frequently Asked Questions (FAQ)
-
Q: Why do we use the reciprocal when dividing fractions?
- A: Dividing by a fraction is the same as multiplying by its reciprocal because division is the inverse operation of multiplication. Multiplying by the reciprocal essentially "undoes" the division by the original fraction.
-
Q: Can I divide fractions without using the reciprocal?
- A: Yes, you can use the common denominator method, as explained above, which provides a more intuitive approach for some learners.
-
Q: What if the fractions are mixed numbers?
- A: Convert the mixed numbers into improper fractions before applying any of the methods discussed. For example, 2 1/2 would become 5/2.
-
Q: What if the result is an improper fraction?
- A: An improper fraction (where the numerator is larger than the denominator) is a perfectly acceptable answer. However, you may choose to convert it into a mixed number for easier interpretation depending on the context.
-
Q: Is there a way to check my answer?
- A: Yes! You can check your answer by multiplying your result by the original divisor. If the product equals the original dividend, your answer is correct. In our example, 4 1/2 (or 9/2) multiplied by 1/6 should equal 3/4. (9/2) * (1/6) = 9/12 = 3/4.
Conclusion: Mastering Fraction Division – A Stepping Stone to Success
Dividing fractions, particularly a problem like 3/4 divided by 1/6, may seem challenging at first, but by understanding the underlying principles and applying the appropriate methods, it becomes a straightforward process. Whether you prefer the reciprocal method for its efficiency or the common denominator approach for its intuitive nature, consistent practice will solidify your understanding. Mastering fraction division is not merely about solving problems; it's about developing a deeper understanding of mathematical concepts and building a solid foundation for more advanced mathematical endeavors. Remember to practice regularly, explore different methods, and visualize the concepts to truly grasp the power and practicality of fraction division. The journey to mathematical fluency begins with mastering these fundamental building blocks.
Latest Posts
Latest Posts
-
21 100 As A Decimal
Sep 22, 2025
-
Square Root Of 300 Simplified
Sep 22, 2025
-
Ten Thousandths As A Decimal
Sep 22, 2025
-
What Angle Is 60 Degrees
Sep 22, 2025
-
Convert 100 Minutes To Hours
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.