3 5 Is Equal To
saludintensiva
Sep 17, 2025 · 6 min read
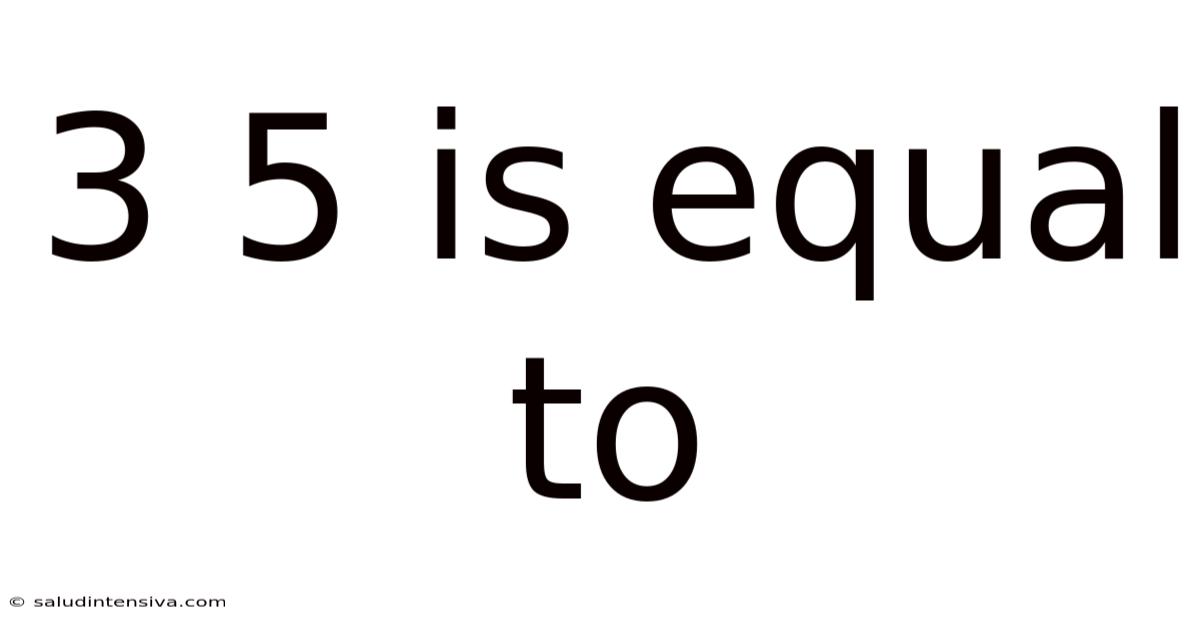
Table of Contents
Decoding 3 = 5: Exploring Mathematical Equivalences and Beyond
The statement "3 = 5" is, at first glance, a blatant falsehood. In standard arithmetic, three is unequivocally not equal to five. However, the seeming simplicity of this statement belies a rich exploration into various mathematical concepts, logical fallacies, and even the nature of truth itself. This article delves deep into the potential interpretations of this statement, moving beyond the simple arithmetic to explore abstract algebra, conditional statements, and the importance of context in mathematical reasoning.
I. The Obvious Falsity and the Importance of Axioms
In the realm of standard arithmetic, based on the Peano axioms (a foundational system for natural numbers), the statement "3 = 5" is demonstrably false. The Peano axioms define the natural numbers and their fundamental operations, establishing a consistent and rigorous system. Within this system, addition and equality are well-defined operations, and the statement 3 + 2 = 5 is true, while 3 = 5 is false. This falsehood stems from the core axioms which define the unique properties of each number. Any system that claims 3 = 5 would necessarily violate at least one of these fundamental axioms, rendering it inconsistent. Understanding this foundational aspect is crucial before exploring alternative interpretations.
II. Exploring Mathematical Structures Beyond Standard Arithmetic
While "3 = 5" is false in standard arithmetic, mathematics encompasses a vast landscape of structures and systems beyond the familiar natural numbers. Let's explore some possibilities:
-
Modular Arithmetic: In modular arithmetic, numbers "wrap around" after reaching a certain modulus. For example, in modulo 2 arithmetic (mod 2), even numbers are equivalent to 0 and odd numbers are equivalent to 1. In this system, 3 ≡ 1 (mod 2) and 5 ≡ 1 (mod 2), so 3 and 5 are congruent modulo 2. This means they share the same remainder when divided by 2. While not strictly "equal" in the standard sense, they are equivalent within the specific context of modulo 2 arithmetic. This demonstrates that the meaning of equality is context-dependent.
-
Abstract Algebra: Abstract algebra introduces groups, rings, and fields, which are sets equipped with operations that satisfy certain axioms. In some of these algebraic structures, it's possible to define operations where elements might appear "equal" in a certain sense, even if they wouldn't be considered equal in standard arithmetic. For instance, consider a group where the group operation is defined in a non-standard way. It's theoretically possible to construct such a group where the elements representing "3" and "5" are equivalent under the group operation. However, this requires a very specific and carefully defined algebraic structure, far removed from the usual understanding of numbers.
-
Fuzzy Logic: Fuzzy logic deals with degrees of truth, rather than absolute true or false statements. In fuzzy logic, a statement like "3 is approximately equal to 5" might be assigned a truth value between 0 and 1, reflecting the degree of similarity or closeness between the two numbers. The closer the numbers, the higher the truth value. This approach acknowledges that the concept of equality can be graded or imprecise, particularly in real-world applications.
III. Logical Fallacies and Misinterpretations
The assertion "3 = 5" is often employed in logical fallacies to demonstrate flawed reasoning. Let's examine some common examples:
-
Division by Zero: A classic example of a false proof often involves an illegal division by zero. A common trick might start with a seemingly true statement and manipulate it through illegal operations (like dividing by zero) to arrive at the absurd conclusion 3 = 5. This highlights the critical importance of following the rules of arithmetic and algebra precisely.
-
Hidden Assumptions: Some "proofs" rely on unstated or hidden assumptions that are subtly flawed. These assumptions might involve incorrect manipulations of variables or misinterpretations of mathematical symbols, leading to a logically invalid conclusion. A critical analysis of every step in a mathematical argument is necessary to identify such hidden flaws.
IV. The Importance of Context and Precision in Mathematics
The exploration of "3 = 5" underscores the critical importance of context and precision in mathematics. The meaning of equality, and indeed the meaning of any mathematical statement, depends heavily on the underlying mathematical system or framework being used. A statement that is false in one system might be true or even meaningful in another.
For instance, the statement "3 apples = 5 oranges" is clearly false if we're considering the number of fruits. However, if we're comparing the value of the fruits in a specific market, it could theoretically be true under certain pricing conditions. This demonstrates how the same statement can have different truth values depending on the context and the units of measurement being used.
V. Beyond Numbers: The Conceptual Equality
The discussion extends beyond mere numerical equality. The statement "3 = 5" can be interpreted metaphorically or conceptually. In some contexts, we might use such a statement to represent a symbolic equivalence or a deliberate simplification for the sake of argument or illustration.
For example, in a simplified model of a complex system, we might assign the value "3" to represent a particular state or condition, and the value "5" to represent another state. If these states are considered functionally equivalent in that simplified model, we might use "3 = 5" as a shorthand notation, understanding that this equality holds only within the confines of the specific model and does not reflect numerical equivalence in the real world.
VI. Addressing Common Misconceptions
Several misconceptions surround the concept of mathematical equality. Let’s clarify some common points of confusion:
-
Approximation vs. Equality: It's crucial to distinguish between approximate equality (≈) and exact equality (=). While 3 might be approximately equal to 5 in some specific context (for instance, when dealing with rounded values), this is different from a strict statement of equality.
-
Equality as a Relation: Equality is a fundamental mathematical relation. It's a binary relation (a relationship between two objects) that satisfies certain properties (reflexivity, symmetry, and transitivity). Understanding these properties helps in assessing the validity of any equality statement.
VII. Conclusion: The Richness of Mathematical Inquiry
While the statement "3 = 5" is a falsehood within standard arithmetic, its analysis reveals a wealth of insights into the nature of mathematics itself. It encourages us to appreciate the diversity of mathematical systems, the importance of precise language and rigorous reasoning, and the context-dependency of mathematical truths. The seeming simplicity of this statement opens doors to exploring modular arithmetic, abstract algebra, fuzzy logic, and the subtle nuances of logical fallacies. It serves as a powerful reminder of the richness and complexity of mathematical inquiry and the importance of critical thinking in all aspects of mathematics. It’s not just about numbers; it’s about understanding the underlying principles and the flexible nature of mathematical concepts. By exploring the limitations and potential interpretations of such a seemingly simple statement, we deepen our understanding of mathematical systems and the profound power of mathematical reasoning. The seemingly trivial "3 = 5" ultimately becomes a gateway to a deeper appreciation of the beauty and complexity of mathematics.
Latest Posts
Latest Posts
-
6 7 As A Decimal
Sep 17, 2025
-
12 100 As A Percentage
Sep 17, 2025
-
67 M2 To Square Feet
Sep 17, 2025
-
50 Deg Fahrenheit To Celsius
Sep 17, 2025
-
43 Degrees Fahrenheit In Celsius
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.