3 5 Is Equivalent To
saludintensiva
Sep 18, 2025 · 6 min read
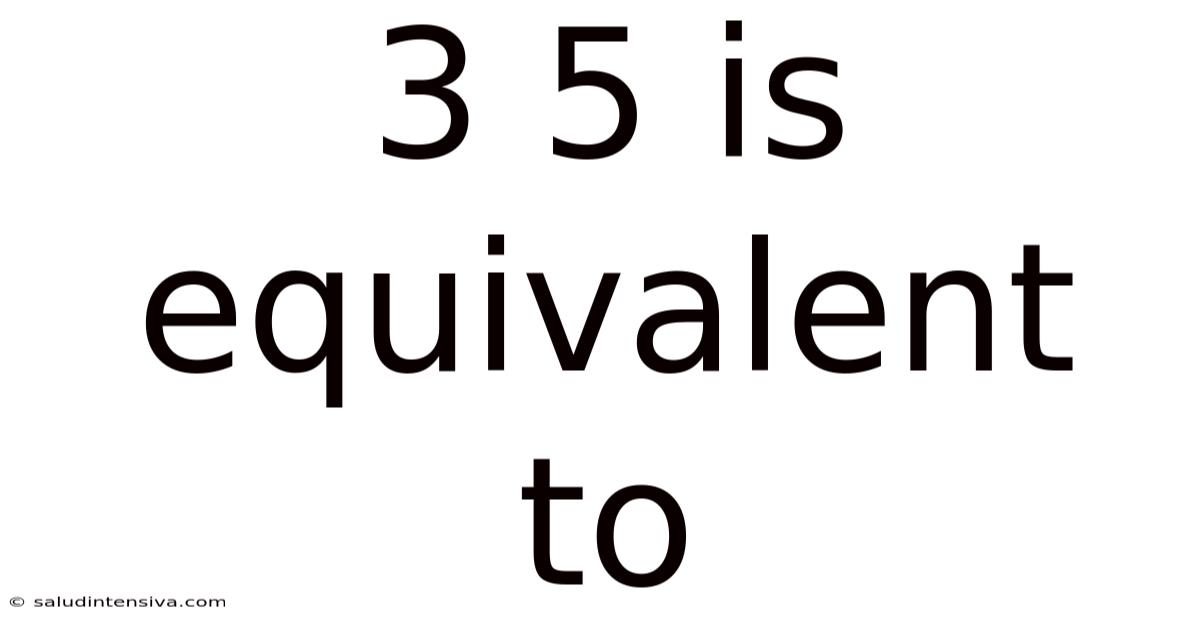
Table of Contents
Decoding 3/5: Exploring Equivalence, Fractions, Decimals, and Percentages
The seemingly simple fraction 3/5 holds a wealth of mathematical understanding within its concise form. Understanding its equivalence unlocks doors to various mathematical concepts, from basic arithmetic to more complex calculations. This article delves deep into the meaning of 3/5, exploring its equivalent forms in decimals, percentages, and other fractions, and clarifying the underlying principles. We'll unpack its representation, provide practical examples, and address common misconceptions. Whether you're a student grasping foundational math or someone looking to refresh your understanding of fractions, this comprehensive guide will illuminate the multifaceted nature of 3/5.
Understanding Fractions: A Quick Refresher
Before diving into the equivalence of 3/5, let's briefly revisit the fundamentals of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number (in this case, 3) indicates how many parts we have.
- Denominator: The bottom number (in this case, 5) indicates the total number of equal parts the whole is divided into.
Therefore, 3/5 means we have 3 parts out of a total of 5 equal parts.
Finding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same value, even though they look different. This is achieved by multiplying or dividing both the numerator and the denominator by the same non-zero number. Think of it like resizing a pizza: If you cut a pizza into 5 slices and take 3, it's the same as cutting the same pizza into 10 slices and taking 6 (both represent 60% of the pizza).
Let's find some equivalent fractions for 3/5:
- Multiplying by 2: (3 x 2) / (5 x 2) = 6/10
- Multiplying by 3: (3 x 3) / (5 x 3) = 9/15
- Multiplying by 4: (3 x 4) / (5 x 4) = 12/20
- Multiplying by 5: (3 x 5) / (5 x 5) = 15/25
And so on. All these fractions – 6/10, 9/15, 12/20, 15/25, etc. – are equivalent to 3/5. They represent the same proportion or quantity. This principle of equivalence is crucial in simplifying fractions and performing various mathematical operations.
Converting 3/5 to a Decimal: The Division Approach
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 3/5:
3 ÷ 5 = 0.6
Therefore, 3/5 is equivalent to 0.6. This decimal representation provides a different but equally valid way of expressing the same value. It's particularly useful in calculations involving decimal numbers or when comparing values in decimal form.
Expressing 3/5 as a Percentage: Scaling to 100
Percentages represent parts per hundred. To convert a fraction to a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%.
0.6 x 100% = 60%
So, 3/5 is equivalent to 60%. This form is commonly used to represent proportions or ratios in various contexts, particularly in statistics, finance, and everyday life.
Visualizing 3/5: A Pictorial Representation
Visual aids can significantly enhance understanding. Imagine a rectangular bar divided into 5 equal parts. Shading 3 of those parts visually represents the fraction 3/5. This visualization helps to grasp the concept of a part of a whole more intuitively. Similarly, you can use circles, squares, or any other shape divided into equal parts to represent the fraction.
Applications of 3/5 Equivalence in Real-World Scenarios
The equivalence of 3/5 finds applications in diverse real-world situations:
- Cooking: If a recipe calls for 3/5 of a cup of sugar, you could use 0.6 cups or 60% of a cup instead.
- Sales and Discounts: A 60% discount is equivalent to a reduction of 3/5 of the original price.
- Statistics: If 3 out of 5 people prefer a particular brand, this represents a 60% preference rate.
- Geometry: When dealing with proportions in shapes, the concept of equivalence plays a crucial role.
Simplifying Fractions: Reducing to the Lowest Terms
While we've explored creating equivalent fractions by multiplying, it's also important to know how to simplify fractions by dividing. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. In the case of 3/5, both 3 and 5 are prime numbers, meaning their only factors are 1 and themselves. Therefore, 3/5 is already in its simplest form.
Comparing Fractions: Determining Greater or Lesser Values
Understanding equivalent fractions is critical when comparing fractions with different denominators. To compare, you need to find a common denominator for both fractions, thereby converting them into equivalent fractions with the same denominator. Then, simply compare the numerators.
Beyond the Basics: Advanced Applications
The concept of equivalent fractions extends to more complex mathematical concepts such as:
- Algebra: Solving equations involving fractions requires manipulating and simplifying fractions, often using the principles of equivalent fractions.
- Calculus: Derivatives and integrals often involve working with fractional expressions where understanding equivalent forms is crucial for simplification and calculation.
Frequently Asked Questions (FAQ)
Q: Is 3/5 a proper or improper fraction?
A: 3/5 is a proper fraction because the numerator (3) is smaller than the denominator (5).
Q: How can I easily convert a fraction to a decimal?
A: Divide the numerator by the denominator using a calculator or long division.
Q: What is the simplest form of 3/5?
A: 3/5 is already in its simplest form because 3 and 5 share no common factors other than 1.
Q: Can I convert 3/5 to a mixed number?
A: No, you cannot convert 3/5 to a mixed number because it's a proper fraction (the numerator is less than the denominator). Mixed numbers are used to represent improper fractions where the numerator is greater than or equal to the denominator.
Q: Are there any other ways to represent 3/5 besides as a fraction, decimal, and percentage?
A: You could represent it visually, using diagrams as mentioned above. You can also express it as a ratio (3:5).
Q: Why is understanding equivalent fractions important?
A: Understanding equivalent fractions is fundamental for comparing fractions, simplifying calculations, solving equations, and understanding proportions in various contexts.
Conclusion: The Significance of 3/5 Equivalence
The seemingly simple fraction 3/5 offers a rich tapestry of mathematical concepts. Its various equivalent forms – decimal (0.6), percentage (60%), and other equivalent fractions (6/10, 9/15, etc.) – illustrate the flexibility and power of fractional representation. Mastering the concept of equivalence is crucial for building a strong foundation in mathematics and applying these principles to real-world problems across diverse fields. This understanding extends beyond basic arithmetic, proving indispensable in more advanced mathematical studies and applications. By grasping the equivalence of 3/5, you unlock a deeper understanding of fractions, decimals, percentages, and their interconnectedness within the broader field of mathematics.
Latest Posts
Latest Posts
-
Ones Tens Hundreds Thousands Chart
Sep 18, 2025
-
1 3 To The Second Power
Sep 18, 2025
-
7 4 As A Fraction
Sep 18, 2025
-
3 4 Plus 1 4
Sep 18, 2025
-
32 Deg C To Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Is Equivalent To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.