3 7 X 2 3
saludintensiva
Sep 20, 2025 · 5 min read
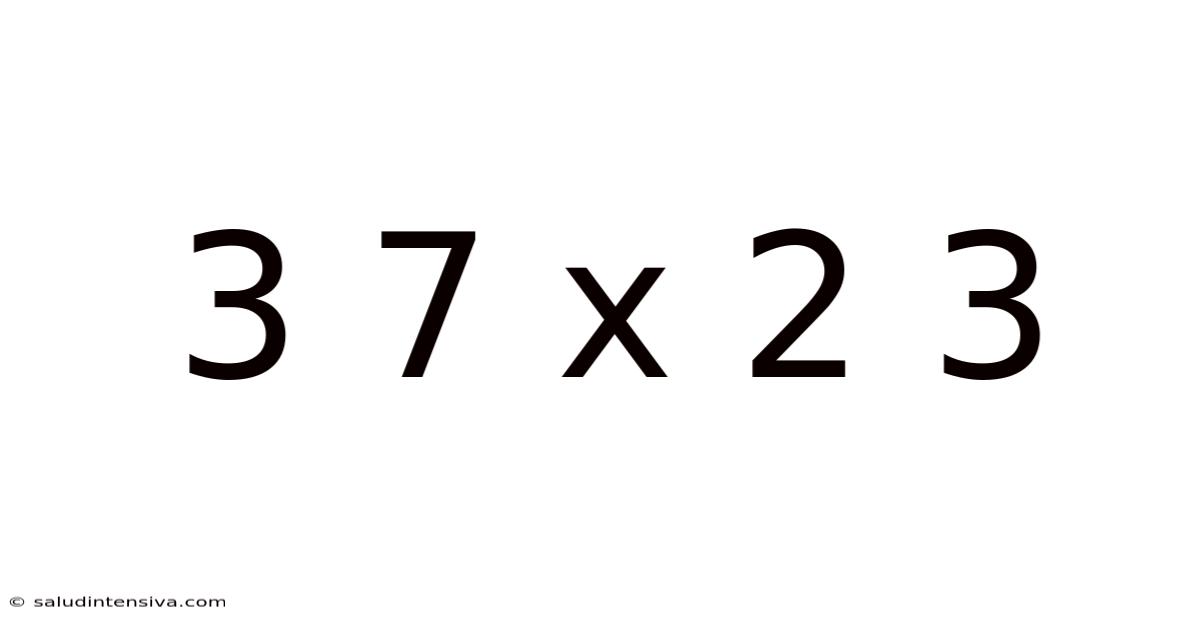
Table of Contents
Unveiling the Mystery: A Deep Dive into 37 x 23
The seemingly simple multiplication problem, 37 x 23, hides a wealth of mathematical concepts and techniques. This seemingly straightforward calculation offers a gateway to understanding fundamental arithmetic principles, different methods of multiplication, and even the underlying logic behind our number system. This article will explore this problem in depth, going beyond a simple answer to reveal the rich tapestry of mathematical ideas woven into its fabric. We'll explore various methods of solving this problem, delve into the underlying mathematical principles, and address common questions and misconceptions.
Introduction: More Than Just a Calculation
At its core, 37 x 23 represents a fundamental operation in arithmetic: multiplication. It signifies the repeated addition of 37, twenty-three times, or equivalently, the repeated addition of 23, thirty-seven times. However, understanding 37 x 23 goes far beyond simply arriving at a numerical answer. It provides an opportunity to explore different approaches to multiplication, offering insight into the versatility and elegance of mathematics. This problem allows us to solidify our understanding of place value, the distributive property, and the efficiency of different calculation methods. By the end of this article, you'll not only know the answer but also grasp the underlying principles and appreciate the beauty of mathematical processes.
Method 1: Standard Long Multiplication
This is the method most commonly taught in schools. It systematically breaks down the multiplication into smaller, manageable steps based on place value.
-
Set up the problem: Write 37 above 23, aligning the digits according to their place value (ones, tens).
37
x23
2. **Multiply by the ones digit:** Multiply 37 by 3 (the ones digit of 23).
37 x23
111 (37 x 3)
3. **Multiply by the tens digit:** Multiply 37 by 20 (the tens digit of 23). Notice we add a zero as a placeholder to account for the tens place.
37 x23
111 740 (37 x 20)
4. **Add the partial products:** Add the two results together.
37 x23
111 740
851
Therefore, 37 x 23 = **851**.
### Method 2: Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to our problem by breaking down the numbers:
37 x 23 = 37 x (20 + 3) = (37 x 20) + (37 x 3)
1. **Calculate 37 x 20:** This is equivalent to 37 x 2 x 10 = 74 x 10 = 740
2. **Calculate 37 x 3:** This equals 111
3. **Add the results:** 740 + 111 = **851**
This method highlights the underlying principle that multiplication is essentially a shortcut for repeated addition and demonstrates the power of breaking down complex problems into simpler components.
### Method 3: Lattice Multiplication
Lattice multiplication is a visually appealing and less error-prone method, especially for larger numbers.
1. **Create a lattice:** Draw a grid with two rows (for the two digits of 37) and two columns (for the two digits of 23).
2. **Fill the cells:** Multiply each digit pair and write the result in the corresponding cell, with the tens digit above the diagonal and the ones digit below.
2 | 3
3 | 06| 09 7 | 14| 21
3. **Sum the diagonals:** Add the numbers along each diagonal, starting from the bottom right. Carry-over digits are added to the next diagonal.
2 | 3
3 | 06| 09 7 | 14| 21
1 | 5 | 1 (851)
The final result, read from top to bottom along the diagonals, is **851**.
### Method 4: Mental Math Techniques
For those comfortable with mental arithmetic, various strategies can streamline the calculation. One approach is to break down the numbers into more manageable parts:
37 x 23 ≈ (40 - 3) x (20 + 3) ≈ (40 x 20) + (40 x 3) - (3 x 20) - (3 x 3) = 800 + 120 - 60 - 9 = 851
This method uses approximation and then adjusts for the overestimation or underestimation. Practicing mental math techniques enhances numerical fluency and provides a deeper understanding of number relationships.
### The Mathematical Underpinnings: Place Value and the Distributive Property
The success of all these methods relies on two fundamental mathematical concepts:
* **Place Value:** Our decimal number system is based on place value, where each digit represents a power of 10. In the number 37, the 3 represents 3 tens (30) and the 7 represents 7 ones (7). Similarly, in 23, the 2 represents 2 tens (20) and the 3 represents 3 ones (3). Understanding place value allows us to break down the multiplication into smaller, manageable steps.
* **Distributive Property:** As illustrated in Method 2, the distributive property is crucial for breaking down the multiplication into simpler components. This property forms the backbone of many algebraic manipulations and is fundamental to understanding how multiplication interacts with addition and subtraction.
### Frequently Asked Questions (FAQ)
* **Why are there different methods for multiplication?** Different methods cater to various learning styles and preferences. Some methods are better suited for mental calculations, while others are more systematic and less prone to errors, especially with larger numbers.
* **Which method is the "best"?** There isn't a single "best" method. The optimal approach depends on individual strengths, the complexity of the problem, and the desired level of accuracy.
* **What if I make a mistake?** Mistakes are opportunities for learning. Carefully review each step, identify the error, and try again. Practice makes perfect.
* **How can I improve my multiplication skills?** Consistent practice is key. Start with simpler problems and gradually increase the difficulty. Explore different methods and find the ones that resonate with you.
### Conclusion: Beyond the Answer
The simple equation 37 x 23 = 851 is more than just a calculation; it's a journey into the heart of arithmetic. By exploring different methods and understanding the underlying principles of place value and the distributive property, we gain a deeper appreciation for the elegance and power of mathematics. This problem serves as a microcosm of the broader mathematical landscape, demonstrating the versatility of approaches and the importance of understanding the 'why' behind the 'how.' The journey of solving this problem enhances our numerical fluency, problem-solving skills, and overall mathematical understanding, preparing us to tackle more complex challenges with confidence and efficiency. Remember, the beauty of mathematics lies not just in finding the answer, but in understanding the process and appreciating the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
1cubic Yard To Cubic Feet
Sep 20, 2025
-
Multiplication Fraction Word Problems Worksheet
Sep 20, 2025
-
11 5 Into A Decimal
Sep 20, 2025
-
Financial Calculator Vs Scientific Calculator
Sep 20, 2025
-
How Tall Is 63 Centimeters
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 7 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.