3 Squared + 4 Squared
saludintensiva
Sep 11, 2025 · 6 min read
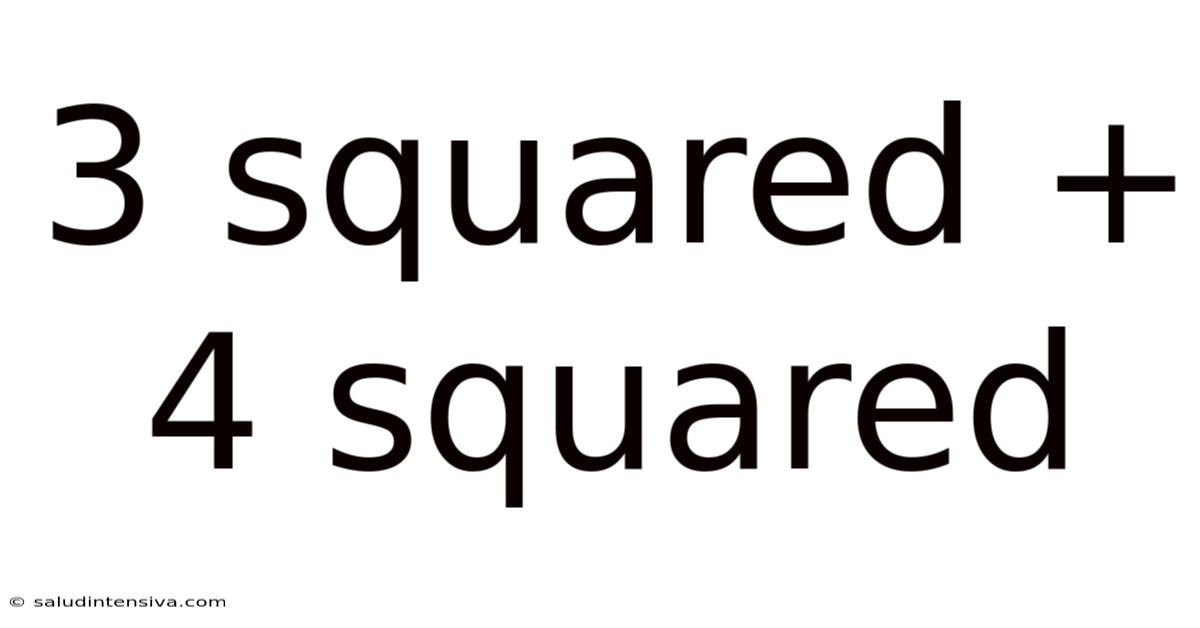
Table of Contents
Decoding 3 Squared + 4 Squared: A Deep Dive into Pythagorean Triples and Beyond
The seemingly simple equation, 3 squared + 4 squared, holds a fascinating place in mathematics. This seemingly straightforward calculation, resulting in 25, opens the door to a world of geometric concepts, algebraic identities, and the elegant beauty of Pythagorean triples. This article will explore this equation in detail, examining its significance, its applications, and its connections to broader mathematical principles. We'll journey from the basic calculation to advanced concepts, ensuring a comprehensive understanding for readers of all levels.
Introduction: Beyond the Basics
At its core, 3 squared + 4 squared is simply a calculation: 3² + 4² = 9 + 16 = 25. However, the significance extends far beyond this basic arithmetic. This equation represents a fundamental example of the Pythagorean theorem, a cornerstone of geometry and trigonometry. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs). In this case, 3 and 4 represent the lengths of the legs, and 5 represents the length of the hypotenuse. This specific combination (3, 4, 5) is the most well-known example of a Pythagorean triple.
Understanding Pythagorean Triples
A Pythagorean triple is a set of three positive integers (a, b, c) that satisfy the Pythagorean theorem: a² + b² = c². The (3, 4, 5) triple is the smallest and most frequently encountered, but infinitely many others exist. These triples are not merely abstract mathematical curiosities; they have practical applications in construction, surveying, and even computer graphics.
Generating Pythagorean Triples: Euclid's Formula
The discovery of an infinite number of Pythagorean triples wasn't a matter of chance. Euclid's formula provides a systematic way to generate them. The formula states that for any two positive integers m and n, where m > n:
- a = m² - n²
- b = 2mn
- c = m² + n²
Let's see how this works. If we let m = 2 and n = 1, we get:
- a = 2² - 1² = 3
- b = 2 * 2 * 1 = 4
- c = 2² + 1² = 5
This reproduces our familiar (3, 4, 5) triple. By varying m and n, we can generate countless other triples. For instance, using m = 3 and n = 2, we obtain the triple (5, 12, 13).
Geometric Interpretation: Right-Angled Triangles
The equation 3² + 4² = 5² has a beautiful geometric interpretation. Imagine a right-angled triangle with legs of length 3 and 4. The Pythagorean theorem guarantees that the hypotenuse will have a length of 5. This relationship is visually compelling and forms the basis for many practical applications. Construction workers, for example, use this principle to ensure the corners of buildings are perfectly square.
Applications in Real World
The applications of Pythagorean triples and the underlying Pythagorean theorem extend far beyond simple geometry:
- Construction and Surveying: Ensuring right angles and accurate measurements in building structures and land surveying. This is crucial for ensuring stability and accuracy in construction projects.
- Navigation: Calculating distances and directions, particularly in systems relying on latitude and longitude coordinates.
- Computer Graphics: Rendering three-dimensional objects on a two-dimensional screen requires extensive use of the Pythagorean theorem to calculate distances and positions.
- Physics and Engineering: Analyzing forces, velocities, and trajectories in many physics and engineering problems often relies on the Pythagorean theorem.
Beyond the (3, 4, 5) Triple: Exploring Other Triples
While (3, 4, 5) is the most well-known, many other Pythagorean triples exist. Here are a few examples generated using Euclid's formula or found through other methods:
- (5, 12, 13): Another relatively small and frequently used triple.
- (8, 15, 17): This triple illustrates the increasing size and complexity of Pythagorean triples.
- (7, 24, 25): This example shows the variety in the ratios between the sides of the triangles.
- (20, 21, 29): This highlights the fact that the numbers within the triples can be very close to each other.
Advanced Concepts: Primitive and Non-Primitive Triples
Pythagorean triples can be categorized as either primitive or non-primitive. A primitive Pythagorean triple is one where the three integers (a, b, c) are coprime, meaning they share no common divisor other than 1. The (3, 4, 5) triple is primitive. A non-primitive Pythagorean triple is one where the three integers share a common divisor greater than 1. For example, (6, 8, 10) is a non-primitive triple, as all three numbers are divisible by 2.
The Equation in Different Number Systems:
While we've primarily discussed the equation within the realm of decimal numbers, it's interesting to consider how it might be represented in other number systems. For example, in binary, 3 is 11, 4 is 100, and 5 is 101. The calculation would involve binary addition and exponentiation, demonstrating the flexibility of the concept across different numerical representations.
Exploring the Equation's Connection to Geometry
The equation 3² + 4² = 5² is visually represented by a right-angled triangle with sides 3, 4, and 5. This connection to geometry gives rise to various geometric problems and constructions that rely on this fundamental relationship. For instance, one can create a visual proof of the Pythagorean theorem using squares built on each side of the triangle, illustrating the area relationships directly.
Frequently Asked Questions (FAQ)
- Q: Is (3, 4, 5) the only Pythagorean triple? A: No, there are infinitely many Pythagorean triples. Euclid's formula provides a method to generate them.
- Q: What is the significance of Pythagorean triples in mathematics? A: They represent a fundamental application of the Pythagorean theorem, connecting algebra and geometry. They also appear in various mathematical fields, such as number theory.
- Q: Are all Pythagorean triples primitive? A: No, many are non-primitive; that is, the numbers share a common factor greater than 1.
- Q: How are Pythagorean triples used in real-world applications? A: They find practical applications in construction, surveying, navigation, computer graphics, and many other fields.
- Q: Can negative numbers be part of a Pythagorean triple? A: No, Pythagorean triples are defined as sets of positive integers.
Conclusion: A Simple Equation, a Vast World
The equation 3 squared + 4 squared, while seemingly simple, unlocks a profound understanding of Pythagorean triples and their connections to geometry, algebra, and various real-world applications. From the basic calculation to the generation of infinite triples using Euclid's formula, the equation showcases the elegance and power of mathematical concepts. Its enduring significance underscores the beauty and practical utility of mathematics in our world. Further exploration into number theory and geometry will reveal even more intricate relationships and applications stemming from this seemingly simple yet fundamental equation. This exploration, hopefully, inspires a deeper appreciation for the rich tapestry of mathematical principles woven into even the most basic mathematical expressions.
Latest Posts
Latest Posts
-
22 9 As A Mixed Number
Sep 12, 2025
-
1 88 Meters To Feet
Sep 12, 2025
-
4 10 In A Decimal
Sep 12, 2025
-
Convert 1 5 To A Fraction
Sep 12, 2025
-
90 Degrees Fahrenheit In Celsius
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 Squared + 4 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.