32/3 As A Mixed Number
saludintensiva
Sep 19, 2025 · 6 min read
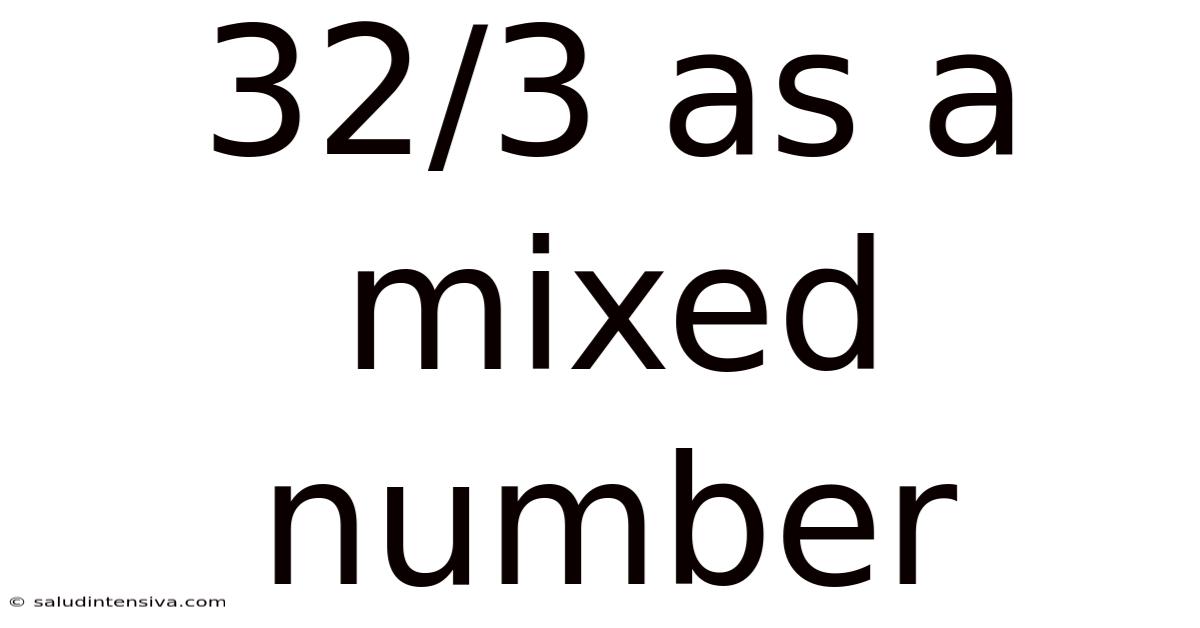
Table of Contents
Understanding 32/3 as a Mixed Number: A Comprehensive Guide
The conversion of improper fractions, like 32/3, into mixed numbers is a fundamental concept in arithmetic. This comprehensive guide will not only show you how to convert 32/3 into a mixed number but also delve into the underlying principles, provide practical examples, and address frequently asked questions. Understanding this process is crucial for mastering fractions and tackling more advanced mathematical concepts. This guide will equip you with the knowledge and confidence to handle similar fraction conversions with ease.
Introduction to Improper Fractions and Mixed Numbers
Before we dive into converting 32/3, let's establish a clear understanding of the terms involved. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and of course, our focus today: 32/3.
A mixed number, on the other hand, combines a whole number and a proper fraction. A proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers provide a more intuitive representation of quantities larger than one. For instance, instead of saying "seven-quarters," we typically say "one and three-quarters" (1 ¾).
Converting 32/3 into a Mixed Number: A Step-by-Step Approach
The conversion process involves dividing the numerator by the denominator. Here’s how to do it for 32/3:
Step 1: Perform the Division
Divide the numerator (32) by the denominator (3):
32 ÷ 3 = 10 with a remainder of 2
Step 2: Identify the Whole Number and the Remainder
The result of the division gives us two crucial pieces of information:
- The quotient (10): This becomes the whole number part of our mixed number.
- The remainder (2): This becomes the numerator of the fractional part of our mixed number.
Step 3: Construct the Mixed Number
The denominator of the fraction in the mixed number remains the same as the denominator of the original improper fraction (3). Therefore, combining the whole number and the fraction from Step 2, we get:
32/3 = 10 ²⁄₃
Therefore, 32/3 expressed as a mixed number is 10 ⅔.
Visualizing the Conversion: A Practical Example
Imagine you have 32 identical cookies, and you want to divide them equally among 3 friends. How many cookies does each friend get?
You can divide 32 cookies by 3 friends: 32 ÷ 3 = 10 with a remainder of 2.
Each friend receives 10 whole cookies (the whole number). You have 2 cookies remaining (the remainder), which you can’t divide equally among the three friends. These 2 cookies represent the fraction 2/3.
So, each friend gets 10 ⅔ cookies. This visually demonstrates the conversion of the improper fraction 32/3 into the mixed number 10 ⅔.
The Reverse Process: Converting a Mixed Number to an Improper Fraction
It's equally important to understand the reverse process—converting a mixed number back into an improper fraction. This is useful for performing calculations involving mixed numbers. Let’s use our example:
Step 1: Multiply the Whole Number by the Denominator
Multiply the whole number (10) by the denominator (3): 10 x 3 = 30
Step 2: Add the Numerator
Add the numerator of the fraction (2) to the result from Step 1: 30 + 2 = 32
Step 3: Construct the Improper Fraction
The result from Step 2 (32) becomes the numerator, and the denominator remains the same (3). Therefore:
10 ²⁄₃ = 32/3
This confirms the equivalence between the mixed number and the improper fraction.
Working with Other Improper Fractions: Applying the Principles
The method described above can be applied to any improper fraction. Let's consider a few more examples:
- 17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ²/₅.
- 25/4: 25 ÷ 4 = 6 with a remainder of 1. Therefore, 25/4 = 6 ¼.
- 41/6: 41 ÷ 6 = 6 with a remainder of 5. Therefore, 41/6 = 6 ⁵⁄₆.
Notice that in each case, we follow the same steps: divide, identify the whole number and remainder, and construct the mixed number.
The Mathematical Rationale Behind the Conversion
The conversion process is based on the fundamental principle of fraction representation. An improper fraction represents a quantity larger than one. By dividing the numerator by the denominator, we separate the whole number units contained within the fraction from the remaining fractional part.
This is essentially a form of long division applied to fractions. The quotient represents the number of whole units, and the remainder represents the portion of a whole unit left over.
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert improper fractions to mixed numbers?
A1: Mixed numbers often provide a more intuitive and easily understandable representation of quantities. They are also more convenient for certain calculations and comparisons. For example, it's easier to visualize 2 ½ pizzas than 5/2 pizzas.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, all improper fractions can be converted to mixed numbers. This is because the numerator is always larger than or equal to the denominator, guaranteeing at least one whole unit.
Q3: What if the remainder is zero after the division?
A3: If the remainder is zero, it means the improper fraction is a whole number. For example, 12/3 = 4. There’s no fractional part in this case.
Q4: Are there different methods for converting improper fractions to mixed numbers?
A4: While the division method is the most common and straightforward, there are other approaches, but they all essentially lead to the same result. These alternative methods might involve using visual aids or repeated subtraction. However, the long division method remains the most efficient and widely applicable.
Q5: How can I check if my conversion is correct?
A5: To verify your conversion, simply convert the mixed number back into an improper fraction using the method outlined earlier. If you obtain the original improper fraction, your conversion was accurate.
Conclusion
Converting improper fractions to mixed numbers is a fundamental skill in arithmetic. Mastering this process not only helps in understanding fractional quantities but also forms a solid base for tackling more advanced mathematical concepts. By following the straightforward steps outlined in this guide, and practicing with various examples, you'll quickly gain confidence and proficiency in handling improper fractions and their mixed-number equivalents. Remember the key steps: divide, identify the whole number and remainder, and construct the mixed number. With practice, this process will become second nature. Understanding this core concept is a significant step towards achieving mastery in mathematics.
Latest Posts
Latest Posts
-
15 Percent Into A Fraction
Sep 19, 2025
-
Size Of Acre In Yards
Sep 19, 2025
-
Convert 65 Pounds To Kilograms
Sep 19, 2025
-
1 5 In Simplest Form
Sep 19, 2025
-
Area Of A Nonagon Calculator
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 32/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.