34/9 As A Mixed Number
saludintensiva
Sep 22, 2025 · 6 min read
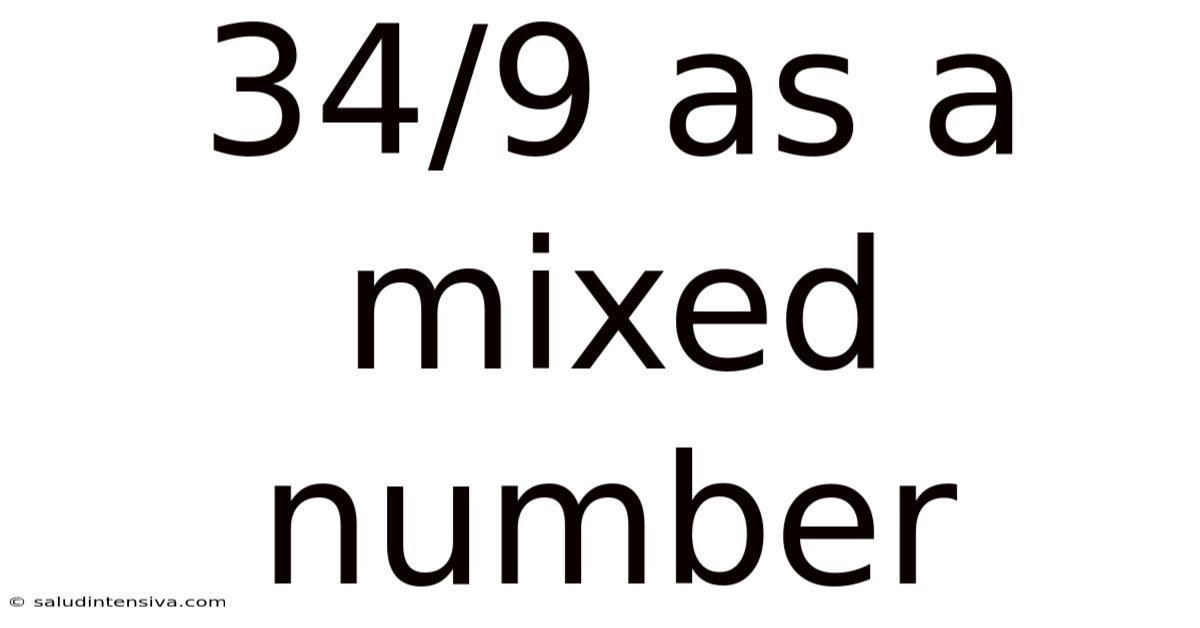
Table of Contents
Understanding 34/9 as a Mixed Number: A Comprehensive Guide
This article will explore the conversion of the improper fraction 34/9 into a mixed number. We'll delve into the process step-by-step, providing a clear understanding of the underlying mathematical concepts. Understanding this conversion is crucial for various mathematical operations and problem-solving, particularly in areas like fractions, decimals, and percentages. We will also examine the practical applications of mixed numbers and address frequently asked questions. This guide aims to provide a comprehensive understanding suitable for students and anyone looking to refresh their knowledge of fraction manipulation.
Introduction: What are Improper Fractions and Mixed Numbers?
Before diving into the conversion of 34/9, let's clarify some fundamental terms. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and, of course, our focus: 34/9. An improper fraction represents a value greater than or equal to one.
A mixed number, on the other hand, consists of a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator (e.g., 3/4, 2/5). Mixed numbers provide a more intuitive representation of values greater than one. For instance, the mixed number 3 3/4 represents three whole units and three-quarters of another unit.
Converting 34/9 to a Mixed Number: A Step-by-Step Guide
The conversion of an improper fraction to a mixed number involves dividing the numerator by the denominator. The quotient (the result of the division) becomes the whole number part of the mixed number. The remainder becomes the numerator of the proper fraction, while the denominator remains the same.
Let's apply this to 34/9:
-
Divide the numerator (34) by the denominator (9): 34 ÷ 9 = 3 with a remainder of 7.
-
The quotient (3) becomes the whole number part of the mixed number.
-
The remainder (7) becomes the numerator of the proper fraction.
-
The denominator (9) remains the same.
Therefore, 34/9 as a mixed number is 3 7/9.
Visualizing the Conversion: A Practical Approach
Imagine you have 34 identical items, and you want to group them into sets of 9. You can create three complete sets of 9 (3 x 9 = 27). This accounts for 27 of your 34 items. You'll have 7 items remaining (34 - 27 = 7). These 7 remaining items represent the 7/9 part of your mixed number. Thus, you have 3 complete sets and 7/9 of another set, confirming our conversion to 3 7/9.
The Importance of Understanding Mixed Numbers
Mixed numbers are essential for various reasons:
-
Clarity and Ease of Understanding: They offer a more intuitive representation of quantities greater than one. It's easier to grasp the concept of 3 7/9 pies than the equivalent 34/9.
-
Real-world Applications: Many real-world measurements and quantities are expressed using mixed numbers. For example, someone might measure a piece of wood as 2 1/2 feet long, rather than 5/2 feet.
-
Problem Solving: In many mathematical problems, using mixed numbers can simplify calculations and make the process more manageable. Adding or subtracting mixed numbers is often easier than working solely with improper fractions.
-
Foundation for Further Mathematical Concepts: A solid understanding of mixed numbers forms the foundation for more advanced concepts like decimal representation, percentage calculations, and even algebraic manipulations.
Beyond the Conversion: Working with Mixed Numbers
Once you've converted an improper fraction to a mixed number, you can perform various operations. Let's consider some examples related to 3 7/9:
-
Addition and Subtraction: To add or subtract mixed numbers, you can either convert them back to improper fractions or work directly with the whole number and fractional parts separately. For example, adding 3 7/9 + 1 2/9 would give you 4 9/9, which simplifies to 5.
-
Multiplication and Division: Multiplying or dividing mixed numbers usually involves converting them into improper fractions first to simplify the calculation. For instance, multiplying 3 7/9 by 2 would involve converting 3 7/9 to 34/9 and then multiplying 34/9 * 2/1 = 68/9. This can then be converted back to a mixed number.
-
Comparing Mixed Numbers: Comparing mixed numbers is straightforward; compare the whole number parts first. If they are equal, then compare the fractional parts.
Explanation of the Underlying Mathematical Principles
The conversion of an improper fraction to a mixed number is fundamentally based on the concept of division and the relationship between the numerator and the denominator. The denominator represents the number of equal parts a whole is divided into, while the numerator represents the number of those parts we have. When the numerator exceeds the denominator, it signifies that we have more than one whole unit. The division process essentially separates the whole units from the remaining fractional part.
Frequently Asked Questions (FAQ)
Q1: Can all improper fractions be converted to mixed numbers?
A1: Yes, all improper fractions can be converted to mixed numbers. This is because an improper fraction inherently represents a value greater than or equal to one, which can always be expressed as a whole number and a fraction.
Q2: Why is it important to learn how to convert improper fractions to mixed numbers?
A2: It's crucial for several reasons: It simplifies calculations, makes problem-solving easier, improves comprehension of quantities, and provides a foundation for more advanced mathematical concepts.
Q3: Are there any shortcuts or tricks to quickly convert improper fractions to mixed numbers?
A3: While there isn't a magical shortcut, practice and familiarity with division will speed up the process. Understanding the relationship between the numerator and the denominator helps you estimate the whole number part before performing the long division.
Q4: What if the remainder is zero after dividing the numerator by the denominator?
A4: If the remainder is zero, it means the improper fraction is a whole number. For example, 18/6 = 3. There is no fractional part in the mixed number.
Q5: Can I convert a mixed number back to an improper fraction?
A5: Absolutely! To do this, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, to convert 3 7/9 back to an improper fraction: (3 * 9) + 7 = 34, so it becomes 34/9.
Conclusion: Mastering the Conversion of 34/9 and Beyond
Converting 34/9 to the mixed number 3 7/9 is a fundamental skill in mathematics. Understanding this conversion isn't just about manipulating numbers; it's about grasping the underlying concepts of fractions, division, and the representation of quantities. This knowledge is crucial for everyday applications and forms the foundation for tackling more complex mathematical problems. By practicing and solidifying your understanding of this conversion, you'll build a stronger mathematical foundation and enhance your problem-solving abilities across various mathematical domains. Remember, the key is practice and consistent application of the learned techniques. Don't hesitate to work through numerous examples to fully internalize the process and confidently tackle similar problems in the future.
Latest Posts
Latest Posts
-
Ten Thousandths As A Decimal
Sep 22, 2025
-
What Angle Is 60 Degrees
Sep 22, 2025
-
Convert 100 Minutes To Hours
Sep 22, 2025
-
Amortization Calculator Interest Only Payments
Sep 22, 2025
-
9 2 Divided By 4
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 34/9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.