34 Percent As A Decimal
saludintensiva
Sep 19, 2025 · 6 min read
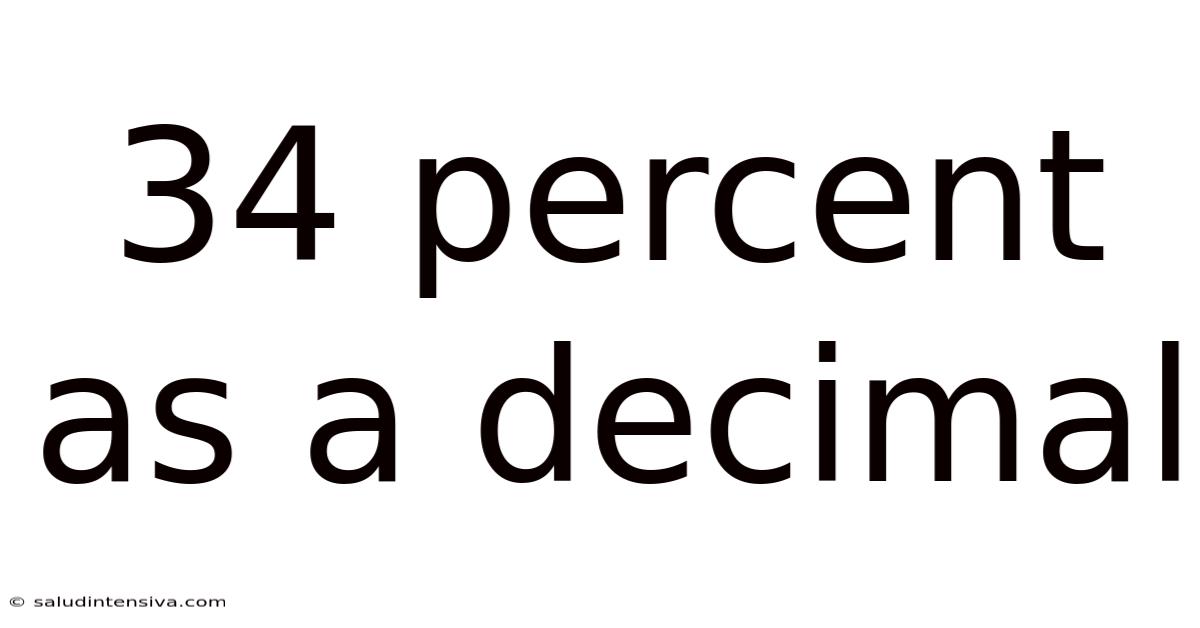
Table of Contents
34 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article provides a comprehensive guide to converting 34 percent to its decimal form, explaining the process, its applications, and addressing frequently asked questions. We'll explore the underlying principles, ensuring you gain a solid grasp of this essential concept.
Understanding Percentages
Before diving into the conversion, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 34% means 34 out of 100, which can be written as the fraction 34/100.
Converting 34% to a Decimal: The Process
Converting a percentage to a decimal is a straightforward process involving a simple division. Since a percentage represents a fraction out of 100, we can directly convert it by dividing the percentage value by 100.
Step 1: Write the percentage as a fraction.
34% can be written as the fraction 34/100.
Step 2: Divide the numerator (top number) by the denominator (bottom number).
Dividing 34 by 100 gives us 0.34.
Therefore, 34% as a decimal is 0.34.
This conversion can also be achieved by moving the decimal point two places to the left. Since every whole number implicitly has a decimal point at the end (e.g., 34 is the same as 34.0), moving the decimal point two places to the left in 34.0 results in 0.34. This shortcut is a quick and efficient method for percentage-to-decimal conversions.
Applications of Decimal Equivalents
Understanding the decimal equivalent of percentages is crucial across numerous fields. Here are a few examples:
-
Finance: Calculating interest rates, discounts, and taxes often requires converting percentages to decimals. For example, if a bank offers a 5% interest rate, it's represented as 0.05 in calculations. Similarly, a 20% discount on a $100 item translates to a $20 discount (0.20 * $100 = $20).
-
Statistics: Percentages are frequently used to represent proportions or probabilities in statistical analysis. Converting percentages to decimals simplifies calculations and interpretations. For instance, if the probability of an event is 75%, it is represented as 0.75 in statistical formulas and models.
-
Science: Many scientific calculations involve percentages, such as expressing concentrations of solutions or measuring changes in physical quantities. Converting to decimals streamlines the calculations and allows for more precise measurements.
-
Everyday Life: From calculating tips in restaurants to understanding sale prices in stores, the ability to convert percentages to decimals is a valuable life skill.
Beyond 34%: Understanding Percentage-to-Decimal Conversions in General
The method used to convert 34% to 0.34 is applicable to any percentage. To convert any percentage to its decimal equivalent, follow these steps:
-
Remove the percent symbol (%).
-
Divide the number by 100. This is equivalent to moving the decimal point two places to the left.
Let's look at some examples:
- 75%: Removing the percent symbol gives 75. Dividing by 100 gives 0.75.
- 12.5%: Removing the percent symbol gives 12.5. Dividing by 100 gives 0.125.
- 250%: Removing the percent symbol gives 250. Dividing by 100 gives 2.5. (Note that percentages greater than 100% result in decimals greater than 1).
- 0.5%: Removing the percent symbol gives 0.5. Dividing by 100 gives 0.005.
Converting Decimals to Percentages
Conversely, converting decimals back to percentages involves the reverse process:
-
Multiply the decimal by 100. This is equivalent to moving the decimal point two places to the right.
-
Add the percent symbol (%).
For example:
- 0.25: Multiplying by 100 gives 25. Adding the percent symbol gives 25%.
- 0.07: Multiplying by 100 gives 7. Adding the percent symbol gives 7%.
- 1.5: Multiplying by 100 gives 150. Adding the percent symbol gives 150%.
Working with Percentages and Decimals in Calculations
Understanding the interchangeability between percentages and decimals is vital for solving mathematical problems involving percentages. It allows you to seamlessly integrate percentage values into equations and formulas. For example, calculating a sales tax of 6% on a $50 purchase can be expressed and solved as:
0.06 * $50 = $3
Understanding the Significance of Place Value
The conversion of 34% to 0.34 highlights the importance of place value in the decimal system. The digit 3 in 0.34 represents 3 tenths (3/10), while the digit 4 represents 4 hundredths (4/100). This understanding is essential for accurately interpreting and manipulating decimal numbers.
Common Mistakes to Avoid
-
Forgetting to divide by 100: A common mistake is directly using the percentage value without dividing by 100. Remember, the percentage represents a fraction out of 100.
-
Incorrect placement of the decimal point: When moving the decimal point, ensure you move it two places to the left (for percentage to decimal) or two places to the right (for decimal to percentage).
-
Misunderstanding percentages greater than 100%: Percentages greater than 100% translate to decimals greater than 1. This represents a value exceeding the original whole.
Frequently Asked Questions (FAQs)
Q1: What is the difference between 34% and 0.34?
A1: They represent the same value, expressed in different forms. 34% is the percentage form, while 0.34 is the decimal form. They are interchangeable in calculations.
Q2: Can I use a calculator to convert 34% to a decimal?
A2: Yes, you can simply enter "34 / 100" into a calculator to get the decimal equivalent, 0.34. Many calculators also have a percentage button that can directly convert percentages to decimals.
Q3: How do I convert a fraction to a percentage and then to a decimal?
A3: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100%. Then, to convert the percentage to a decimal, divide by 100 (or move the decimal point two places to the left).
Q4: Why is understanding percentage-to-decimal conversion important?
A4: It's crucial for various applications, from everyday financial calculations to complex scientific and statistical analyses. It simplifies calculations and enables accurate interpretations of data.
Q5: What if I have a percentage with a fraction (e.g., 34 1/2%)?
A5: First, convert the mixed number percentage to an improper fraction (e.g., 34 1/2% = 69/2%). Then convert this improper fraction to a decimal by dividing the numerator (69) by the denominator (2) to get 34.5. Finally, divide this by 100 to arrive at 0.345.
Conclusion
Converting 34% to its decimal equivalent, 0.34, is a fundamental mathematical skill with wide-ranging applications. Understanding the underlying principles, the conversion process, and the various contexts where these concepts are used is crucial for effective problem-solving in various fields. This guide provided a comprehensive overview, clarifying the process, addressing common misconceptions, and equipping you with the knowledge to confidently handle percentage-to-decimal conversions in the future. Remember the simple steps, practice regularly, and you'll quickly master this essential mathematical skill.
Latest Posts
Latest Posts
-
5 Divided By 1 1 4
Sep 19, 2025
-
All The Multiples Of 16
Sep 19, 2025
-
11 000 Minutes To Hours
Sep 19, 2025
-
3 To The Tenth Power
Sep 19, 2025
-
5000 Sq Ft To Acres
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 34 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.