36/5 As A Mixed Number
saludintensiva
Sep 20, 2025 · 6 min read
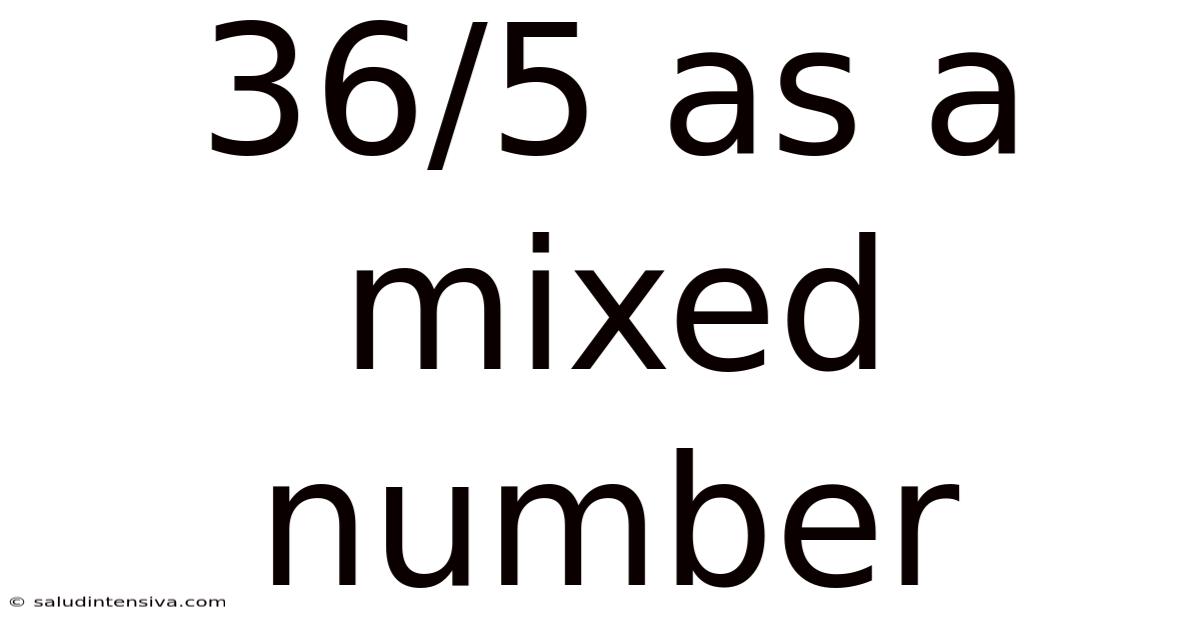
Table of Contents
Understanding 36/5 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 36/5, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 36/5 into a mixed number but also delve into the underlying concepts, provide practical examples, and address frequently asked questions. Understanding this process is crucial for various mathematical operations and problem-solving scenarios. We will explore the concept of mixed numbers, explain the steps involved in the conversion process, provide a scientific explanation, and clarify any common misconceptions. By the end of this article, you'll confidently convert any improper fraction into a mixed number.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit. Mixed numbers are a useful way to represent quantities that are greater than one but not a whole number.
Converting 36/5 to a Mixed Number: A Step-by-Step Guide
The process of converting an improper fraction (where the numerator is larger than or equal to the denominator) to a mixed number involves division. Here's how to convert 36/5:
-
Divide the numerator by the denominator: Divide 36 by 5.
36 ÷ 5 = 7 with a remainder of 1
-
Identify the whole number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 7.
-
Identify the new numerator (remainder): The remainder from the division becomes the numerator of the fraction part of the mixed number. The remainder is 1.
-
Keep the original denominator: The denominator of the fraction remains the same as the original denominator. In this case, it's 5.
-
Combine the whole number and the fraction: Put the whole number and the fraction together to form the mixed number. Therefore, 36/5 as a mixed number is 7 1/5.
Practical Examples: Mastering the Conversion
Let's solidify our understanding with a few more examples:
-
Convert 22/7 to a mixed number:
22 ÷ 7 = 3 with a remainder of 1. Therefore, 22/7 = 3 1/7.
-
Convert 45/8 to a mixed number:
45 ÷ 8 = 5 with a remainder of 5. Therefore, 45/8 = 5 5/8.
-
Convert 100/12 to a mixed number:
100 ÷ 12 = 8 with a remainder of 4. Therefore, 100/12 = 8 4/12. Notice that this fraction can be simplified further to 8 1/3 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 4. Always simplify your fractions to their lowest terms whenever possible.
The Scientific Explanation: Understanding the Underlying Principles
The conversion from an improper fraction to a mixed number is based on the fundamental concept of division and the representation of quantities. An improper fraction represents a quantity larger than one whole unit. By dividing the numerator by the denominator, we are essentially determining how many whole units are contained within the improper fraction. The remainder represents the portion of a whole unit that is left over, expressed as a fraction.
This process can also be visually represented. Imagine you have 36 identical objects. If you want to group them into sets of 5, you can create 7 complete sets (7 x 5 = 35) and have 1 object left over. This visually represents 7 wholes and 1/5 of a whole, reinforcing the mixed number 7 1/5.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process – converting a mixed number back into an improper fraction. This skill is often necessary in more complex mathematical calculations. The steps are as follows:
-
Multiply the whole number by the denominator: Multiply the whole number of the mixed number by the denominator of the fraction.
-
Add the numerator: Add the result from step 1 to the numerator of the fraction.
-
Keep the original denominator: The denominator remains unchanged.
Let's convert 7 1/5 back to an improper fraction:
-
7 (whole number) x 5 (denominator) = 35
-
35 + 1 (numerator) = 36
-
The denominator remains 5.
Therefore, 7 1/5 converts back to 36/5.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert between improper fractions and mixed numbers?
A1: Converting between improper fractions and mixed numbers is essential for various mathematical operations, including addition, subtraction, multiplication, and division of fractions. Mixed numbers offer a more intuitive representation of quantities larger than one, while improper fractions are often more convenient for calculations.
Q2: What if the remainder is zero after dividing the numerator by the denominator?
A2: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 20/5 = 4. There is no fractional part.
Q3: Can I convert any improper fraction into a mixed number?
A3: Yes, you can convert any improper fraction into a mixed number. The process is always the same: divide the numerator by the denominator.
Q4: How do I simplify a fraction in a mixed number?
A4: After converting to a mixed number, simplify the fractional part by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. This reduces the fraction to its lowest terms. For example, 8 4/12 simplifies to 8 1/3 because the GCD of 4 and 12 is 4.
Q5: Are there any online tools or calculators that can help me convert improper fractions to mixed numbers?
A5: While there are many online calculators available, understanding the underlying process is crucial. These tools can be helpful for checking your work but should not replace a thorough grasp of the method itself.
Conclusion: Mastering Fractions – A Stepping Stone to Success
Converting improper fractions like 36/5 into mixed numbers is a cornerstone of fractional arithmetic. The ability to seamlessly transition between these representations is invaluable for further mathematical explorations. By understanding the steps involved, the underlying principles, and addressing common questions, you've gained a solid foundation for confidently tackling more complex fractional problems. Remember to practice regularly and utilize various examples to solidify your understanding. This skill is not just about memorizing steps; it's about developing a deeper understanding of numerical representation and manipulation. Mastering this skill will undoubtedly enhance your problem-solving abilities and contribute to your overall mathematical proficiency.
Latest Posts
Latest Posts
-
1000 Cubic Inches To Liters
Sep 21, 2025
-
180 Degrees Celsius To Fahrenheit
Sep 21, 2025
-
1 3 Of 1 Million
Sep 21, 2025
-
Mach To Kilometers Per Hour
Sep 21, 2025
-
Dares For A 21st Birthday
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 36/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.