3x 1 10x X 4
saludintensiva
Sep 22, 2025 · 5 min read
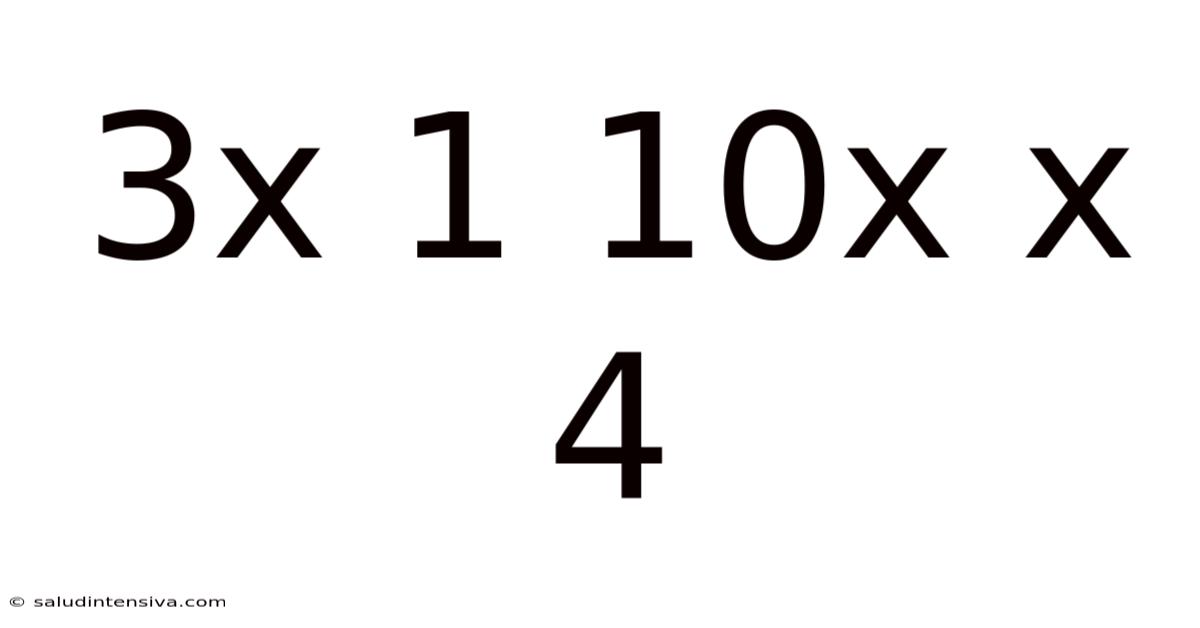
Table of Contents
Deconstructing the Mathematical Puzzle: 3x + 1 = 10x + 4
This article delves into the seemingly simple yet surprisingly complex mathematical equation: 3x + 1 = 10x + 4. We'll explore how to solve this equation, understand the underlying principles, and even touch upon its relevance in broader mathematical contexts. This isn't just about finding the value of 'x'; it's about understanding the process and appreciating the elegance of algebraic manipulation. Whether you're a student brushing up on your algebra skills or simply curious about the world of equations, this comprehensive guide will provide a thorough understanding.
Understanding Linear Equations
Before jumping into the solution, let's establish a foundational understanding. The equation 3x + 1 = 10x + 4 is a linear equation. This means that the highest power of the variable 'x' is 1. Linear equations represent straight lines when graphed on a coordinate plane. Solving such equations involves manipulating them algebraically to isolate the variable 'x' on one side of the equation.
Step-by-Step Solution: Solving for 'x'
Solving this equation is a straightforward application of algebraic principles. Our goal is to isolate 'x' and determine its numerical value. Here's a step-by-step breakdown:
-
Combine like terms: The first step involves moving all the terms containing 'x' to one side of the equation and the constant terms (numbers without 'x') to the other side. We can achieve this by subtracting 3x from both sides:
3x + 1 - 3x = 10x + 4 - 3x
This simplifies to:
1 = 7x + 4
-
Isolate the term with 'x': Next, we isolate the term containing 'x' by subtracting 4 from both sides:
1 - 4 = 7x + 4 - 4
This simplifies to:
-3 = 7x
-
Solve for 'x': Finally, we solve for 'x' by dividing both sides by 7:
-3 / 7 = 7x / 7
Therefore:
x = -3/7
This is the solution to the equation. The value of 'x' that satisfies the equation 3x + 1 = 10x + 4 is -3/7.
Verification: Checking the Solution
It's always a good practice to verify your solution. Let's substitute x = -3/7 back into the original equation:
3(-3/7) + 1 = 10(-3/7) + 4
-9/7 + 1 = -30/7 + 4
Converting 1 and 4 to fractions with a denominator of 7:
-9/7 + 7/7 = -30/7 + 28/7
-2/7 = -2/7
Since both sides of the equation are equal, our solution x = -3/7 is correct.
The Broader Context: Applications of Linear Equations
Linear equations, like the one we just solved, are fundamental building blocks in various fields. They find applications in:
-
Physics: Describing relationships between physical quantities like velocity, acceleration, and time. For example, calculating the distance traveled by an object with constant acceleration involves linear equations.
-
Engineering: Modeling systems and predicting behavior. Linear equations are crucial in structural analysis, circuit design, and many other engineering disciplines.
-
Economics: Analyzing supply and demand, predicting market trends, and modeling economic growth. Linear equations provide a simplified yet powerful tool for understanding these complex systems.
-
Computer Science: Developing algorithms and solving problems related to optimization, resource allocation, and data analysis. Linear algebra, a more advanced field built upon linear equations, is particularly important in machine learning and artificial intelligence.
-
Finance: Calculating interest, projecting investments, and analyzing financial risks. Linear equations help in creating financial models and making informed investment decisions.
Expanding the Understanding: Systems of Linear Equations
While the equation 3x + 1 = 10x + 4 is a single linear equation, we often encounter systems of linear equations. These involve multiple equations with multiple variables. Solving systems of linear equations can be approached using various techniques such as substitution, elimination, or matrix methods. These techniques are essential in many advanced mathematical and scientific applications.
Beyond Linearity: Exploring Non-Linear Equations
While this article focuses on linear equations, it's important to note that many real-world phenomena are best modeled using non-linear equations. These equations contain variables raised to powers greater than 1 or involve more complex functions. Solving non-linear equations often requires more sophisticated techniques, and sometimes analytical solutions are not even possible. Numerical methods are often employed to approximate solutions for these types of equations.
Frequently Asked Questions (FAQ)
Q: Can this equation be solved graphically?
A: Yes, absolutely! You can graph both lines, y = 3x + 1 and y = 10x + 4, on a coordinate plane. The point where the two lines intersect represents the solution to the equation. The x-coordinate of this intersection point will be -3/7.
Q: What if the equation was slightly different, say 3x + 1 = 10x + 5? Would the solution process be similar?
A: Yes, the solution process would be very similar. The only difference would be the numerical values involved in the calculations. Following the same steps as above, you would arrive at a different solution for 'x'.
Q: Are there any other methods to solve this linear equation?
A: While the method explained above is the most straightforward, you could also use other algebraic manipulation techniques to reach the same solution. The core principle remains the same: isolate the variable 'x' using valid algebraic operations.
Q: What if I encounter an equation where there's no solution or infinitely many solutions?
A: In some cases, linear equations may have no solution (parallel lines) or infinitely many solutions (overlapping lines). This happens when the coefficients of the variables and the constants result in an inconsistency or an identity.
Conclusion: Mastering the Fundamentals
Solving the equation 3x + 1 = 10x + 4 may seem like a small step, but it's a fundamental exercise that builds a strong foundation in algebra. Understanding linear equations and the process of solving them is crucial for tackling more complex mathematical problems. This skill isn't just limited to academic settings; it's a transferable skill with broad applications in diverse fields. By mastering these basic principles, you're laying the groundwork for deeper exploration into the fascinating world of mathematics and its real-world applications. The journey of mathematical understanding begins with these seemingly simple equations, paving the way for more advanced concepts and problem-solving abilities. Remember to practice regularly and explore different approaches to solidify your grasp of the subject.
Latest Posts
Latest Posts
-
X 2 1 0 Solution
Sep 22, 2025
-
Concrete Demolition And Removal Cost
Sep 22, 2025
-
Acre Feet To Cubic Yards
Sep 22, 2025
-
0 2 As A Fraction
Sep 22, 2025
-
Convert 1500 M To Feet
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3x 1 10x X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.