3x 2 9x 30 0
saludintensiva
Sep 22, 2025 · 5 min read
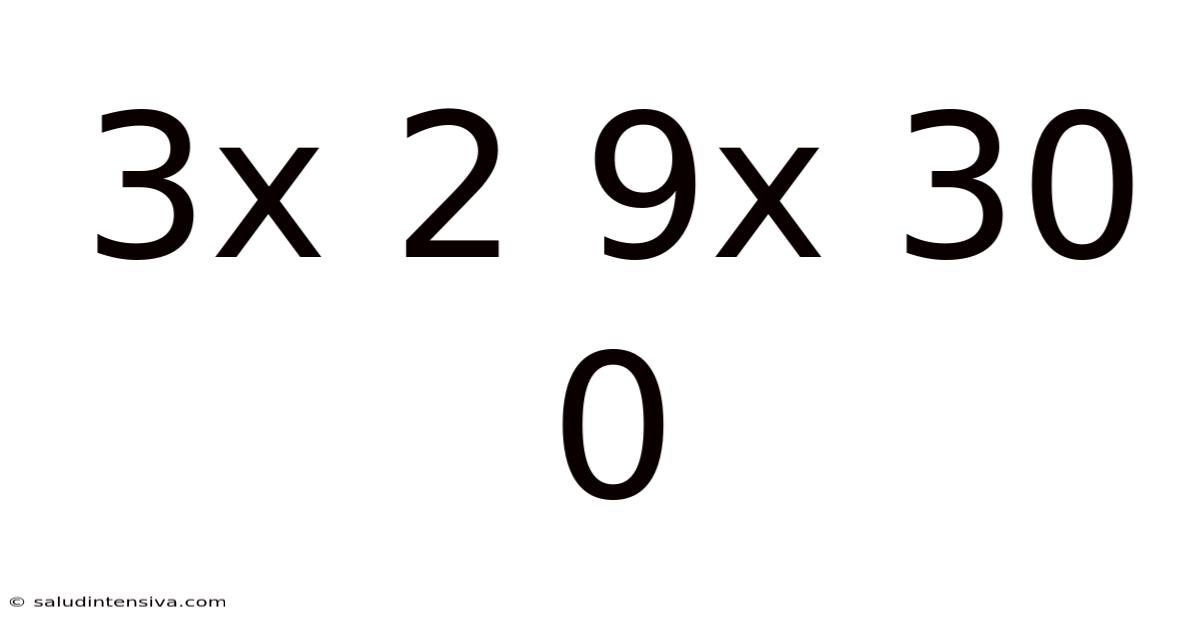
Table of Contents
Decoding the Mystery: Exploring the Pattern in 3x2, 9x30, and 0
This article delves into the intriguing numerical sequence: 3 x 2, 9 x 30, and 0. While seemingly disparate at first glance, a closer examination reveals potential underlying patterns and mathematical relationships. We'll explore various interpretations, considering arithmetic progressions, geometric progressions, and even possibilities within modular arithmetic. This investigation will not only decipher the immediate sequence but also equip you with the tools to approach similar numerical puzzles. Understanding these patterns helps build a stronger foundation in mathematical reasoning and problem-solving.
I. Initial Observations and Potential Interpretations
The given sequence, 3 x 2, 9 x 30, and 0, presents an immediate challenge. The expressions "3 x 2" and "9 x 30" represent multiplication operations, resulting in 6 and 270 respectively. The presence of "0" as the third element introduces an element of asymmetry and requires careful consideration.
Several initial interpretations could be considered:
-
Arithmetic Progression: An arithmetic progression is a sequence where the difference between consecutive terms is constant. The difference between 6 and 270 is 264, which makes an arithmetic progression unlikely. The inclusion of 0 further complicates this possibility.
-
Geometric Progression: A geometric progression is a sequence where each term is found by multiplying the previous term by a constant value (the common ratio). The ratio between 6 and 270 is 45, but this relationship doesn't extend to the third term, 0. Therefore, a straightforward geometric progression is also improbable.
-
Hidden Operations or Patterns: The most likely interpretation is that there's a more complex underlying pattern or hidden operation connecting the three elements. This might involve multiple operations, consideration of prime factors, or even a relationship based on the digits themselves.
II. Exploring Potential Mathematical Relationships
Let's explore various avenues to potentially uncover the pattern:
A. Analyzing the Results:
The results of the multiplications are 6 and 270. Let's analyze their prime factorizations:
- 6 = 2 x 3
- 270 = 2 x 3<sup>3</sup> x 5
Observing the prime factorization, we see a common factor of 2 and 3. The presence of 5 in the factorization of 270 might hint at a possible pattern involving the multiplication of prime numbers or their powers. However, the inclusion of 0 significantly complicates this approach.
B. Examining the Numbers as Sequences:
Let's look at the individual numbers involved: 3, 2, 9, 30, and 0. Is there a sequence within these numbers themselves?
- We can consider the progression of the first multipliers: 3 and 9 (a simple 3 times increase).
- The second multipliers exhibit a more complex progression: 2 and 30. There isn't an obvious arithmetic or geometric relationship between these two numbers.
C. Considering Modular Arithmetic:
Modular arithmetic involves performing arithmetic operations within a specific modulus (a positive integer). For example, modulo 3 means we only consider the remainders after division by 3. While there's no immediately apparent modulus that directly connects these values, exploring modular arithmetic with different moduli could potentially reveal hidden patterns.
D. Investigating Digit Manipulation:
We can consider manipulating the digits of the numbers involved. For example:
- Sum of digits: 3 + 2 = 5; 9 + 3 + 0 = 12. No immediate pattern emerges.
- Product of digits: 3 x 2 = 6; 9 x 3 x 0 = 0. The results are 6 and 0, still requiring further analysis.
III. Potential Scenarios and Hypotheses
Given the complexities, several hypotheses could explain the sequence:
Hypothesis 1: A Recursive or Iterative Pattern:
It is possible that the sequence follows a recursive or iterative rule. Each element might depend on the previous one or multiple preceding elements according to some mathematical formula. Defining this formula would require additional information or a clearer pattern.
Hypothesis 2: A Context-Dependent Sequence:
The sequence might only make sense within a specific context. Perhaps it's an excerpt from a larger mathematical problem, a coding sequence, or a real-world scenario where the numbers represent specific quantities or measurements. Without further context, the meaning remains ambiguous.
Hypothesis 3: A Sequence with Gaps or Missing Elements:
The three elements might be part of a larger sequence with missing terms. It's possible that additional data points are needed to reveal the true nature of the underlying progression.
Hypothesis 4: An Arbitrary or Random Sequence:
In the absence of any discernible pattern, it is possible that the sequence is essentially arbitrary or random. There might be no deeper mathematical relationship connecting these three elements. This hypothesis should only be considered after exhaustively exploring all other possibilities.
IV. The Role of the Zero
The inclusion of zero is a particularly intriguing aspect of this sequence. Zero's unique properties in mathematics often signal a change, a termination point, or a reset within a mathematical system. In this case, the presence of zero could mean:
- Termination: The sequence ends with zero, suggesting a completion or conclusion.
- Reset: Zero could signal a restart or the beginning of a new pattern.
- Placeholder: Zero might be a placeholder for a missing term or an undefined value.
V. Expanding the Exploration: Methods and Tools
To further investigate the pattern, we could employ more advanced mathematical tools and techniques:
- Statistical Analysis: Analyzing the sequence statistically might reveal trends or correlations that are not immediately apparent.
- Computer Programming: Writing a program to generate sequences based on various hypothetical rules could help test different patterns and identify possibilities.
- Mathematical Software: Specialized mathematical software can assist in identifying patterns and relationships in numerical data.
VI. Conclusion: The Ongoing Search for Patterns
The sequence 3 x 2, 9 x 30, and 0 presents a captivating challenge in mathematical pattern recognition. While we have explored several potential avenues—arithmetic and geometric progressions, prime factorization, modular arithmetic, and digit manipulation—no definitive pattern has emerged. The presence of zero adds an extra layer of complexity, suggesting potential termination, reset, or placeholder interpretations. To definitively solve this puzzle, more information or context might be necessary. However, the exploration itself highlights the importance of systematically investigating numerical sequences, utilizing various mathematical tools and approaches, and fostering critical thinking in problem-solving. The quest to decipher the mystery of this seemingly simple sequence serves as a valuable exercise in mathematical reasoning and problem-solving skills. This exploration underscores the creativity and persistence required to unravel mathematical puzzles and the inherent beauty of mathematical patterns, even when they remain elusive. Further investigation might involve seeking additional data points, exploring different mathematical models, or considering the potential contextual relevance of the sequence.
Latest Posts
Latest Posts
-
Convert 48 F To Celsius
Sep 22, 2025
-
Simple Interest Calculator In Excel
Sep 22, 2025
-
5200 Sq Ft To Acres
Sep 22, 2025
-
160 Degrees C To F
Sep 22, 2025
-
45 Days From December 16
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 9x 30 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.