3x 4 2x 8 5x
saludintensiva
Sep 23, 2025 · 6 min read
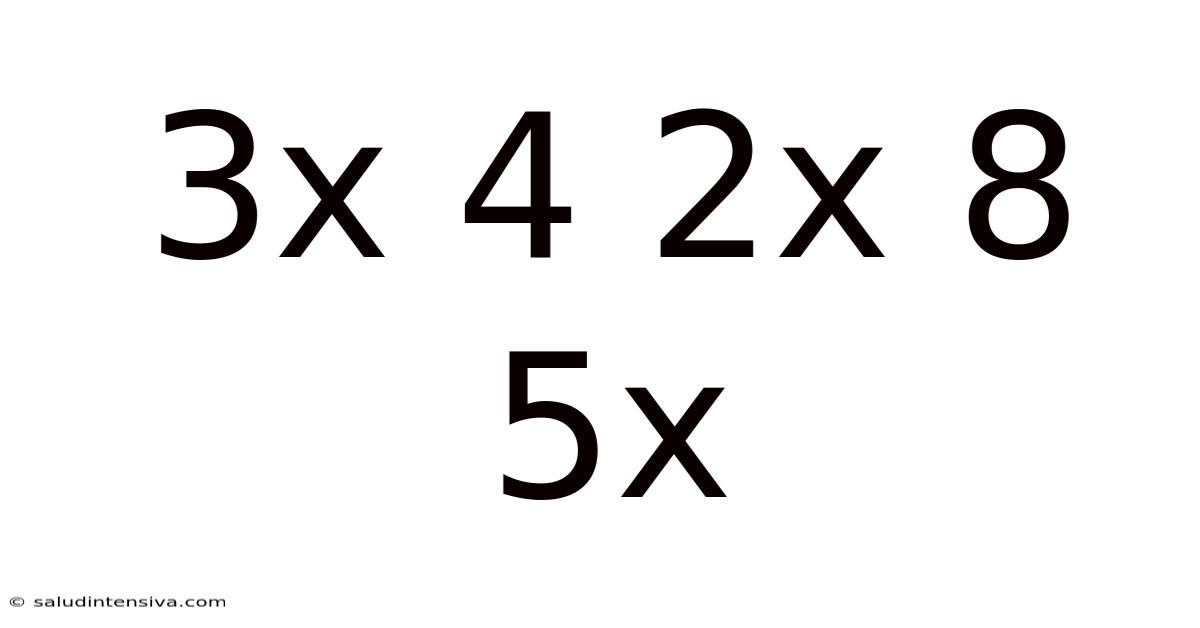
Table of Contents
Decoding the Mystery: Understanding the Sequence 3x4, 2x8, 5x
This article delves into the fascinating puzzle presented by the numerical sequence: 3x4, 2x8, 5x. We'll explore various mathematical approaches to decipher the pattern, discuss potential solutions, and consider the broader implications of pattern recognition in mathematics. Understanding this seemingly simple sequence can unlock valuable insights into logical reasoning and problem-solving skills. This exploration will cover multiple interpretations and approaches, emphasizing critical thinking and analytical skills.
Introduction: The Allure of Pattern Recognition
The human brain is wired to identify patterns. From recognizing faces to predicting weather patterns, our ability to discern order in apparent chaos is fundamental to our survival and understanding of the world. Mathematics, at its core, is the study of patterns. The sequence 3x4, 2x8, 5x presents a concise but intriguing challenge, forcing us to consider various mathematical operations and logical reasoning to determine the underlying rule. This exercise not only improves mathematical skills but also strengthens critical thinking and problem-solving abilities.
Possible Interpretations and Solutions
The beauty of this puzzle lies in its multiple potential solutions, depending on the assumptions we make about the underlying rules. Let's explore several possibilities:
1. The Product Pattern: A Simple Approach
The most straightforward interpretation involves focusing on the product of the numbers in each pair.
- 3 x 4 = 12
- 2 x 8 = 16
Notice that the products increase by 4. Following this pattern, the next product should be 20. Therefore, if we assume the pattern relates to the products, we might consider the equation 5 x y = 20, leading to the solution y = 4. Thus, one possible completion of the sequence is 3x4, 2x8, 5x4. This interpretation is simple and elegant, relying on a consistent arithmetic progression.
2. The Ratio Pattern: A More Complex Relationship
Instead of focusing on the products, let's examine the ratio between the two numbers in each pair.
- 3/4 = 0.75
- 2/8 = 0.25
Here, we observe that the ratios decrease by 0.5. Continuing this pattern, the next ratio should be -0.25. To find the value of x that satisfies this condition, we would solve the equation 5/x = -0.25. This gives us x = -20. Therefore, another possible completion of the sequence is 3x4, 2x8, 5x(-20). This approach demonstrates the importance of considering different mathematical relationships.
3. A Combination of Operations: Exploring Non-Linear Relationships
We can explore more complex scenarios by considering combinations of operations. For instance, we might add the two numbers and then multiply the result by a specific factor. Let's analyze:
- 3 + 4 = 7. If we multiply 7 by 12/7 (approximately 1.71), we get approximately 12.
- 2 + 8 = 10. If we multiply 10 by 16/10 (1.6), we get 16.
This suggests a changing multiplier, possibly reflecting a complex function. The next step would involve identifying that function and extrapolating it to determine the value of x. Such non-linear patterns would require more advanced mathematical techniques and potentially involve curve fitting or regression analysis. This demonstrates the potential for diverse approaches in mathematical problem-solving, and the necessity to think outside the box.
4. Prime Numbers and Their Multipliers: A More Abstract Approach
Let's examine the numbers themselves, focusing on their prime factorizations. This is a more abstract and potentially less intuitive approach, but it opens up the possibility of hidden patterns:
- 3: A prime number. Its multiplier is 4.
- 2: A prime number. Its multiplier is 8.
- 5: A prime number. Its multiplier is yet to be determined.
Observing the multipliers, we notice they are not directly related in a simple arithmetic progression, so a different pattern may be present. Perhaps the pattern lies in the relationship between the prime number and its multiplier. For example, maybe the multiplier is always a multiple of 4, in which case the next multiplier could be 12 (resulting in 5 x 12 = 60), or perhaps there's a sequence within the multipliers themselves (4,8,...). Without more terms, it's difficult to pinpoint this definitively, illustrating that even seemingly simple sequences can hold surprising mathematical depth.
The Importance of Context and Further Data
The lack of additional terms in the sequence makes definitive conclusions difficult. With only three elements, multiple interpretations remain plausible. The inclusion of more terms would considerably narrow down the possibilities and allow for a more rigorous analysis. The solution, then, is inherently dependent on the underlying mathematical operation or rule intended by the originator of the sequence.
Mathematical Tools for Pattern Recognition
Various mathematical tools can aid in identifying patterns in numerical sequences. These include:
- Arithmetic Progressions: Sequences where the difference between consecutive terms is constant.
- Geometric Progressions: Sequences where the ratio between consecutive terms is constant.
- Polynomial Sequences: Sequences that can be expressed as polynomial functions.
- Recurrence Relations: Equations that define each term as a function of previous terms.
- Difference Tables: A method for analyzing sequences by calculating the differences between consecutive terms, then the differences of the differences, and so on.
These tools, coupled with intuitive observation and logical reasoning, are invaluable in solving mathematical puzzles like the sequence presented above.
FAQ (Frequently Asked Questions)
Q: Is there only one correct answer?
A: No, without further context or additional terms, there is not one definitively "correct" answer. Multiple interpretations and solutions are possible, depending on the assumed underlying rules or patterns.
Q: What makes this sequence challenging?
A: The challenge lies in the ambiguity of the pattern. The limited number of terms allows for multiple valid interpretations, requiring careful consideration of various mathematical relationships and the potential for complex or non-linear patterns.
Q: How can I improve my pattern recognition skills?
A: Practice is key. Regularly engage in activities like solving mathematical puzzles, analyzing data sets, and exploring different mathematical concepts. This will help train your brain to identify and understand patterns more efficiently.
Q: Are there similar puzzles I can try?
A: Yes, many mathematical puzzles and number sequences exist online and in textbooks. Searching for terms like "number sequence puzzles," "mathematical pattern recognition," or "logic puzzles" will reveal a variety of challenges to test your skills.
Conclusion: The Value of Exploration and Critical Thinking
The seemingly simple sequence 3x4, 2x8, 5x serves as a powerful reminder of the importance of critical thinking, logical reasoning, and the exploration of multiple mathematical perspectives. While a single, definitive answer may not exist without additional information, the process of attempting to solve this puzzle enhances problem-solving skills and underscores the richness and complexity of mathematical patterns. Remember, the journey of exploration is often as valuable as reaching a final solution. The flexibility in interpreting the sequence emphasizes that mathematical problems often present multiple approaches and interpretations, fostering creativity and encouraging deeper engagement with mathematical concepts. The exploration of this relatively simple sequence can pave the way for understanding more complex mathematical patterns and principles, fostering a strong foundation for mathematical reasoning.
Latest Posts
Latest Posts
-
Standard Form Examples With Answers
Sep 23, 2025
-
Inches To Gallons Conversion Chart
Sep 23, 2025
-
1 3 4 Times 3
Sep 23, 2025
-
90 Days From August 31
Sep 23, 2025
-
Convert 27 Inches To Centimeters
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3x 4 2x 8 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.