4 12 As A Percent
saludintensiva
Sep 14, 2025 · 6 min read
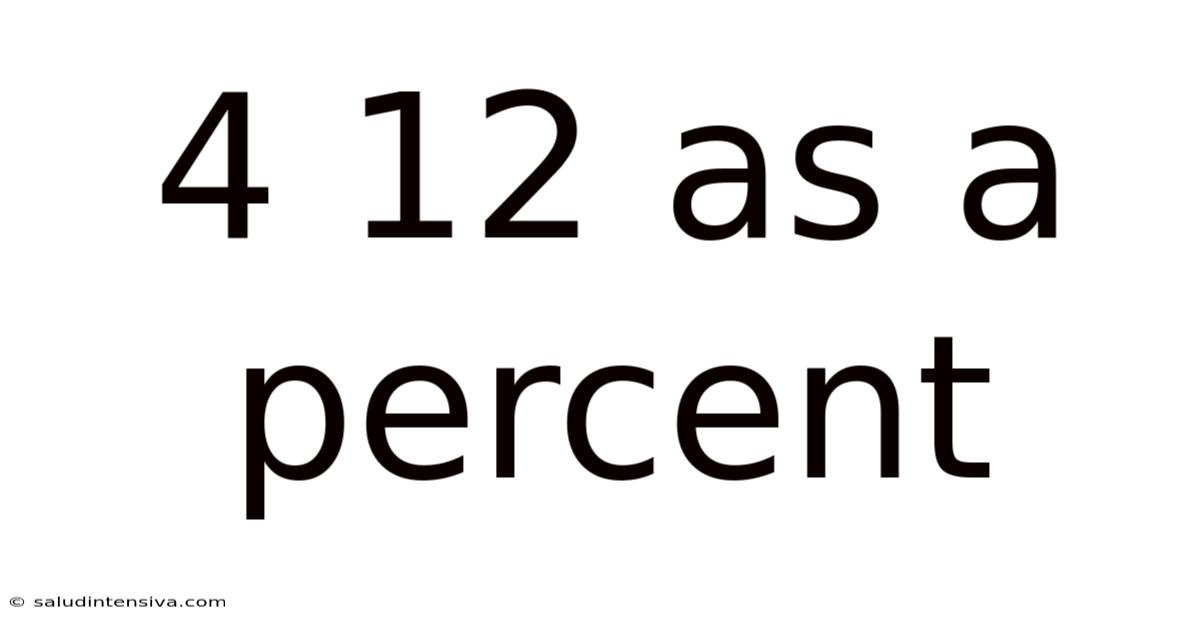
Table of Contents
Understanding 4/12 as a Percentage: A Comprehensive Guide
Many situations in daily life, from calculating discounts to understanding financial reports, require converting fractions into percentages. This article provides a comprehensive guide to understanding how to convert the fraction 4/12 into a percentage, along with explanations, examples, and frequently asked questions. We’ll delve into the underlying mathematical principles and offer practical applications to solidify your understanding.
Introduction: Fractions, Decimals, and Percentages
Before we dive into converting 4/12, let's briefly review the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). For example, 4/12 represents 4 parts out of a total of 12 parts.
-
Decimal: A decimal is a way of expressing a fraction using base-10 notation. It uses a decimal point to separate the whole number part from the fractional part.
-
Percentage: A percentage is a way of expressing a fraction as a portion of 100. It's denoted by the symbol "%". A percentage represents how many parts out of 100 make up the whole.
The ability to convert between these forms is crucial for various mathematical operations and real-world applications.
Converting 4/12 to a Percentage: Step-by-Step Guide
Converting 4/12 to a percentage involves two main steps: simplifying the fraction and then converting the simplified fraction to a percentage.
Step 1: Simplify the Fraction
The fraction 4/12 can be simplified by finding the greatest common divisor (GCD) of the numerator (4) and the denominator (12). The GCD of 4 and 12 is 4. Dividing both the numerator and denominator by 4, we get:
4 ÷ 4 / 12 ÷ 4 = 1/3
This simplified fraction, 1/3, represents the same proportion as 4/12. Simplifying fractions makes the conversion to a percentage much easier.
Step 2: Convert the Simplified Fraction to a Percentage
To convert a fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can achieve this by dividing the numerator by the denominator and multiplying the result by 100.
1 ÷ 3 ≈ 0.3333...
Multiplying this decimal by 100 gives us the percentage:
0.3333... × 100 ≈ 33.33%
Therefore, 4/12 is equal to approximately 33.33%. The three dots (...) indicate that the decimal 0.3333... is a repeating decimal, meaning the digit 3 repeats infinitely. In practical applications, we often round the percentage to a reasonable number of decimal places, such as two decimal places (33.33%).
Mathematical Explanation: The Underlying Principles
The conversion from a fraction to a percentage is fundamentally about expressing a proportion as a part of 100. The formula for converting a fraction (a/b) to a percentage is:
(a/b) × 100%
Where 'a' is the numerator and 'b' is the denominator. This formula directly reflects the concept of expressing a proportion relative to a base of 100. In the case of 4/12, we first simplified it to 1/3, and then applied this formula:
(1/3) × 100% ≈ 33.33%
This process is based on the fundamental principle of equivalent fractions and the definition of a percentage as a fraction out of 100.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages has wide-ranging applications in various fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve converting fractions or decimals to percentages.
-
Statistics: Representing data as percentages is crucial for visualizing and interpreting statistical information, such as survey results or population demographics.
-
Science: Many scientific calculations and measurements involve expressing quantities as percentages, particularly in fields like chemistry and physics.
-
Everyday Life: Calculating tips at restaurants, understanding sale prices in stores, and even comprehending weather reports (e.g., a 30% chance of rain) all require an understanding of percentages.
Real-World Examples: Applying the Concept
Let's look at a few real-world scenarios where converting 4/12 (or its equivalent, 1/3) to a percentage is useful:
Example 1: Sales Discount
A store offers a discount of 4/12 on a product. This means the discount is 33.33% off the original price. If the original price is $60, the discount amount is:
$60 × 0.3333 ≈ $20
The final price after the discount would be $40.
Example 2: Test Scores
A student answered 4 out of 12 questions correctly on a quiz. Their score is 1/3 or approximately 33.33%.
Example 3: Survey Results
In a survey of 12 people, 4 preferred a particular brand. The percentage of people who preferred that brand is 33.33%.
Frequently Asked Questions (FAQ)
Q: Is there a quicker way to convert 1/3 to a percentage without a calculator?
A: While the method of dividing and multiplying by 100 is accurate, for 1/3, you can remember that 1/3 is approximately 33.33%. It’s a commonly used fraction, so memorizing its percentage equivalent is helpful.
Q: What if the fraction isn't easily simplified?
A: If the fraction is not easily simplified, use a calculator to divide the numerator by the denominator and then multiply the result by 100 to find the percentage.
Q: What's the difference between a repeating decimal and a terminating decimal?
A: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.75). A repeating decimal has digits that repeat infinitely (e.g., 0.333...).
Q: Can I convert percentages back to fractions?
A: Yes, to convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 33.33% becomes 33.33/100, which can be approximated as 1/3.
Q: Are there any online tools or calculators to help with these conversions?
A: While this article aims to provide a comprehensive understanding, various online calculators and conversion tools are readily available to perform these calculations quickly. However, understanding the underlying principles remains crucial for effective problem-solving.
Conclusion: Mastering Percentage Conversions
Converting fractions like 4/12 to percentages is a fundamental skill with broad applicability. By understanding the steps involved—simplifying the fraction and then applying the conversion formula—you can confidently tackle various percentage-related problems in diverse settings. Remember that the ability to convert between fractions, decimals, and percentages is not just about mathematical accuracy; it's about developing a deeper understanding of proportions and their practical significance in the real world. Mastering this skill will significantly enhance your ability to analyze data, solve problems, and navigate various aspects of daily life.
Latest Posts
Latest Posts
-
3 To The 6 Power
Sep 15, 2025
-
What Is 6 9 Reduced
Sep 15, 2025
-
What Time Is 20 45
Sep 15, 2025
-
Lcm Of 14 And 10
Sep 15, 2025
-
48 Acres To Sq Ft
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 4 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.