4 12 In Lowest Terms
saludintensiva
Sep 17, 2025 · 5 min read
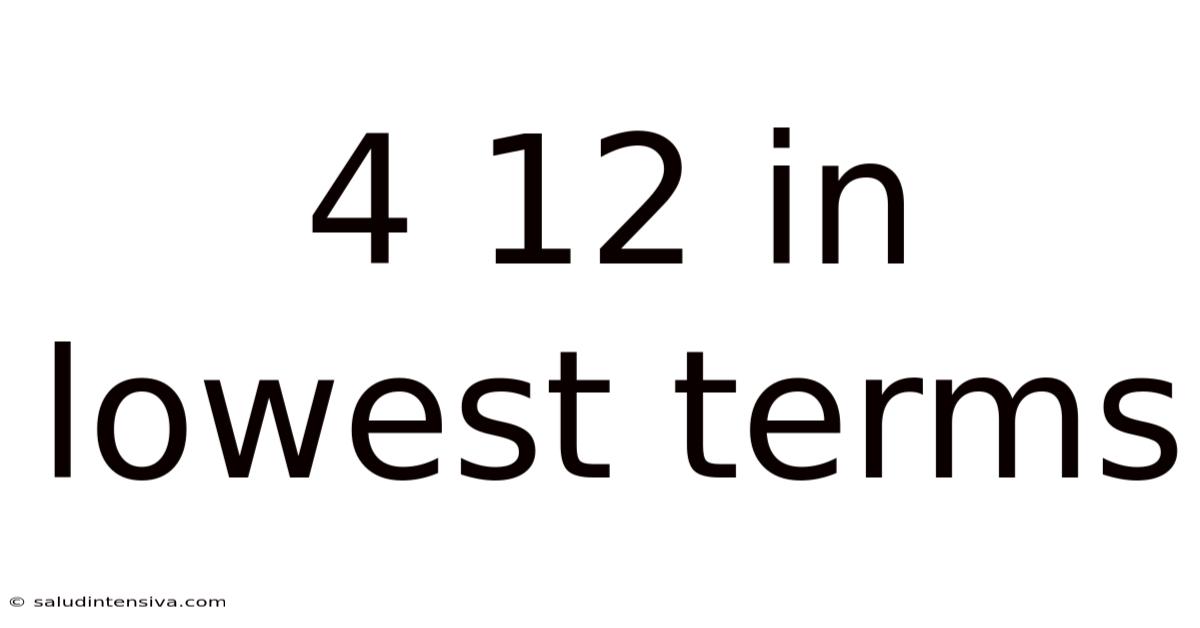
Table of Contents
Simplifying Fractions: Understanding 4/12 in Lowest Terms
Finding the simplest form of a fraction is a fundamental concept in mathematics, crucial for understanding proportions, ratios, and various other mathematical operations. This article will comprehensively explore the simplification of the fraction 4/12, explaining the process step-by-step, delving into the underlying mathematical principles, and addressing frequently asked questions. We'll also explore how this seemingly simple concept applies to more complex scenarios. Understanding this process will build a strong foundation for more advanced mathematical concepts.
Introduction to Fraction Simplification
A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. For example, in the fraction 4/12, 4 is the numerator and 12 is the denominator. Simplifying a fraction means reducing it to its lowest terms—a form where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and use in calculations. Simplifying fractions is essentially finding an equivalent fraction that is in its simplest form.
Finding the Greatest Common Factor (GCF)
The key to simplifying fractions lies in identifying the Greatest Common Factor (GCF) of the numerator and denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder. To find the GCF of 4 and 12, we can list the factors of each number:
- Factors of 4: 1, 2, 4
- Factors of 12: 1, 2, 3, 4, 6, 12
By comparing the lists, we see that the largest number that appears in both lists is 4. Therefore, the GCF of 4 and 12 is 4.
Simplifying 4/12 to Lowest Terms
Once we've found the GCF, we simplify the fraction by dividing both the numerator and the denominator by the GCF. In this case:
4 ÷ 4 = 1 12 ÷ 4 = 3
Therefore, 4/12 simplified to its lowest terms is 1/3. This means that 4/12 and 1/3 represent the same proportion or part of a whole.
Alternative Methods for Finding the GCF
While listing factors works well for smaller numbers, it becomes less efficient with larger numbers. Here are two alternative methods for finding the GCF:
1. Prime Factorization: This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factors are 2 x 2 = 4, which is the GCF.
2. Euclidean Algorithm: This algorithm is particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 4 and 12:
- Divide 12 by 4: 12 = 4 x 3 + 0
Since the remainder is 0, the GCF is the divisor, which is 4.
Visual Representation of Fraction Simplification
Imagine you have a pizza cut into 12 equal slices. If you have 4 slices, you have 4/12 of the pizza. Simplifying 4/12 to 1/3 means grouping the 4 slices into a single larger group representing one-third of the whole pizza. This visual representation helps to understand that both fractions represent the same quantity.
Applying Fraction Simplification in Real-World Scenarios
Simplifying fractions isn't just an abstract mathematical exercise. It has practical applications in many real-world situations:
- Cooking: A recipe calls for 4/12 cups of sugar; simplifying to 1/3 cup makes measuring easier.
- Construction: Calculations involving measurements often involve fractions that need to be simplified for accuracy.
- Finance: Working with percentages and proportions frequently requires simplifying fractions.
- Data Analysis: Simplifying fractions is often needed to interpret and present data clearly.
Beyond 4/12: Simplifying More Complex Fractions
The same principles apply to simplifying more complex fractions. For instance, let's consider the fraction 24/36:
-
Find the GCF: The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36. The GCF is 12.
-
Simplify: 24 ÷ 12 = 2; 36 ÷ 12 = 3.
Therefore, 24/36 simplified to its lowest terms is 2/3.
Understanding Equivalent Fractions
Simplifying a fraction doesn't change its value; it only changes its representation. 4/12, 2/6, and 1/3 are all equivalent fractions because they represent the same proportion. This concept is fundamental to understanding operations with fractions, such as addition and subtraction, where finding a common denominator often involves working with equivalent fractions.
Frequently Asked Questions (FAQ)
Q: What if the numerator and denominator are prime numbers?
A: If the numerator and denominator are both prime numbers (and different), the fraction is already in its lowest terms. For example, 2/7 cannot be simplified further.
Q: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
A: Yes, but it's more efficient to divide by the greatest common factor. Dividing by smaller common factors will require multiple steps to reach the lowest terms.
Q: What happens if the numerator is larger than the denominator?
A: This is called an improper fraction. You can simplify it in the same way as a proper fraction. Alternatively, you can convert it to a mixed number (a whole number and a fraction). For example, 16/4 simplifies to 4/1, or simply 4.
Q: Are there any online tools or calculators for simplifying fractions?
A: Yes, numerous online tools and calculators can simplify fractions automatically. However, understanding the underlying principles is crucial for developing mathematical proficiency.
Conclusion: Mastering Fraction Simplification
Simplifying fractions to their lowest terms is a critical skill in mathematics. Understanding the concept of the GCF, using various methods to find it, and recognizing equivalent fractions are all vital components. This article has explored these concepts in detail, offering various approaches to tackling fraction simplification and providing insights into its real-world applications. By mastering this fundamental skill, you build a solid foundation for more advanced mathematical concepts and problem-solving. Remember, practice is key to becoming proficient in simplifying fractions. The more you practice, the more confident and efficient you'll become.
Latest Posts
Latest Posts
-
3 5 As An Improper Fraction
Sep 17, 2025
-
9 10 Into A Decimal
Sep 17, 2025
-
Is 29 Prime Or Composite
Sep 17, 2025
-
26 Out Of 40 Percentage
Sep 17, 2025
-
How Many Minutes Is 120
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 12 In Lowest Terms . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.