4 5 As A Percent
saludintensiva
Sep 12, 2025 · 5 min read
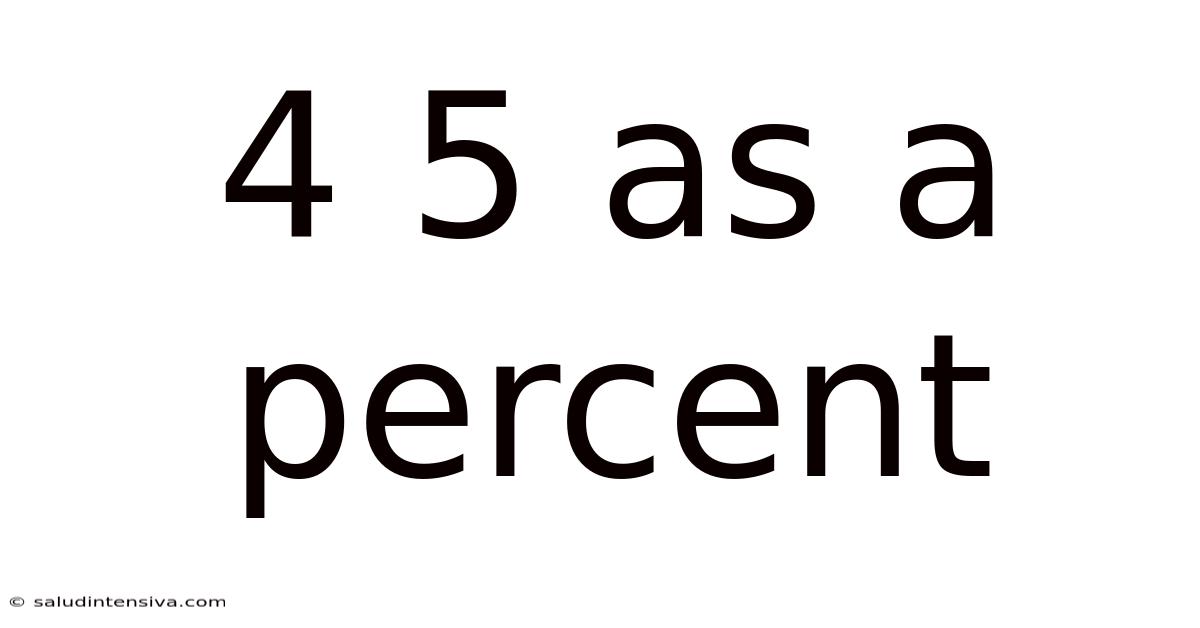
Table of Contents
Understanding 4/5 as a Percent: A Comprehensive Guide
What is 4/5 as a percent? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with widespread applications in everyday life. This comprehensive guide will not only answer the question directly but also equip you with the tools and knowledge to confidently convert any fraction into a percentage. We'll explore the underlying principles, provide step-by-step examples, delve into the practical applications, and address frequently asked questions.
Introduction: Fractions, Decimals, and Percentages
Before tackling the conversion of 4/5 to a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 4/5 means 4 parts out of a total of 5 parts.
-
Decimals: Represent a part of a whole using a base-10 system. The decimal point separates the whole number from the fractional part. For instance, 0.75 represents seventy-five hundredths.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" denotes percentage. For example, 75% means 75 parts out of 100 parts.
These three forms are interchangeable; you can convert one to another using specific methods. Understanding these conversions is crucial for various mathematical operations and real-world applications.
Converting 4/5 to a Percentage: Step-by-Step Guide
There are two primary methods to convert the fraction 4/5 into a percentage:
Method 1: Converting the Fraction to a Decimal First
This method involves two steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (4) by the denominator (5): 4 ÷ 5 = 0.8
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.8 × 100 = 80%. Therefore, 4/5 is equal to 80%.
Method 2: Direct Conversion using the Percentage Formula
This method utilizes the fundamental percentage formula:
(Part / Whole) × 100% = Percentage
In our case:
- Part = 4
- Whole = 5
Substituting these values into the formula:
(4 / 5) × 100% = 0.8 × 100% = 80%
Both methods yield the same result: 4/5 is equivalent to 80%.
Understanding the Result: What does 80% mean?
80% represents 80 parts out of 100 equal parts. Imagine a pie cut into 100 slices. 80% would represent 80 of those slices. This concept is fundamental to understanding proportions and ratios.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating Discounts: A store offers a 20% discount on an item. Understanding percentages allows you to calculate the actual discount amount.
-
Analyzing Test Scores: Your test score is represented as a fraction (e.g., 15/20). Converting this fraction to a percentage gives you a clear understanding of your performance.
-
Understanding Financial Data: Financial reports often use percentages to represent growth rates, profit margins, and other key metrics.
-
Estimating Quantities: If a recipe calls for 75% of a cup of flour, you can easily calculate the required amount.
-
Comparing Proportions: Percentages allow for easy comparison of different proportions. For example, comparing the percentage of students who passed an exam in different classes.
Beyond 4/5: Converting Other Fractions to Percentages
The methods described above can be applied to convert any fraction to a percentage. Let's look at a few more examples:
-
Converting 3/4 to a percentage:
- Method 1: 3 ÷ 4 = 0.75; 0.75 × 100% = 75%
- Method 2: (3/4) × 100% = 75%
-
Converting 1/2 to a percentage:
- Method 1: 1 ÷ 2 = 0.5; 0.5 × 100% = 50%
- Method 2: (1/2) × 100% = 50%
-
Converting 7/10 to a percentage:
- Method 1: 7 ÷ 10 = 0.7; 0.7 × 100% = 70%
- Method 2: (7/10) × 100% = 70%
Dealing with Improper Fractions
Improper fractions (where the numerator is larger than the denominator) can also be converted to percentages. For example, let's convert 7/4 to a percentage:
- Convert to a decimal: 7 ÷ 4 = 1.75
- Convert to a percentage: 1.75 × 100% = 175%
Notice that the percentage is greater than 100%. This is perfectly acceptable and indicates that the fraction represents more than a whole.
Scientific Explanation: Ratio and Proportion
At its core, converting a fraction to a percentage is about understanding ratio and proportion. A fraction represents a ratio between two quantities (the numerator and the denominator). A percentage expresses this ratio as a proportion of 100. The process of conversion is essentially scaling the ratio to a common denominator of 100.
Frequently Asked Questions (FAQ)
Q1: Why is converting fractions to percentages useful?
A1: Percentages provide a standardized way to compare different fractions and proportions. They are easier to understand and interpret in many contexts than fractions.
Q2: Can I convert a percentage back to a fraction?
A2: Yes! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% becomes 60/100, which simplifies to 3/5.
Q3: What if the denominator of the fraction is a large number?
A3: The methods remain the same. You can still divide the numerator by the denominator to get the decimal equivalent and then multiply by 100 to obtain the percentage. A calculator can be very helpful in these situations.
Q4: What if I have a mixed number (e.g., 1 1/2)?
A4: First convert the mixed number to an improper fraction (e.g., 1 1/2 becomes 3/2). Then, follow the steps outlined above to convert the improper fraction to a percentage.
Q5: Are there any online calculators that can help with these conversions?
A5: Yes, numerous online calculators are available to convert fractions to percentages and vice versa. However, understanding the underlying principles is crucial for a deeper mathematical understanding.
Conclusion: Mastering Percentage Conversions
Converting 4/5 to a percentage, and understanding the broader concept of fraction-to-percentage conversion, is a fundamental skill in mathematics. This process involves understanding the relationships between fractions, decimals, and percentages, and applying straightforward calculations. By mastering these concepts, you'll gain a powerful tool for tackling various mathematical problems and real-world situations. Remember, practice is key to solidifying your understanding and building confidence in your ability to perform these conversions quickly and accurately. The more you practice, the more intuitive these conversions will become.
Latest Posts
Latest Posts
-
Lcm Of 11 And 10
Sep 12, 2025
-
180 Days From April 15
Sep 12, 2025
-
Convert Bar Pressure To Psi
Sep 12, 2025
-
16 To The Second Power
Sep 12, 2025
-
Find Missing Side Of Parallelogram
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 4 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.