4 9 X 1 7
saludintensiva
Sep 15, 2025 · 5 min read
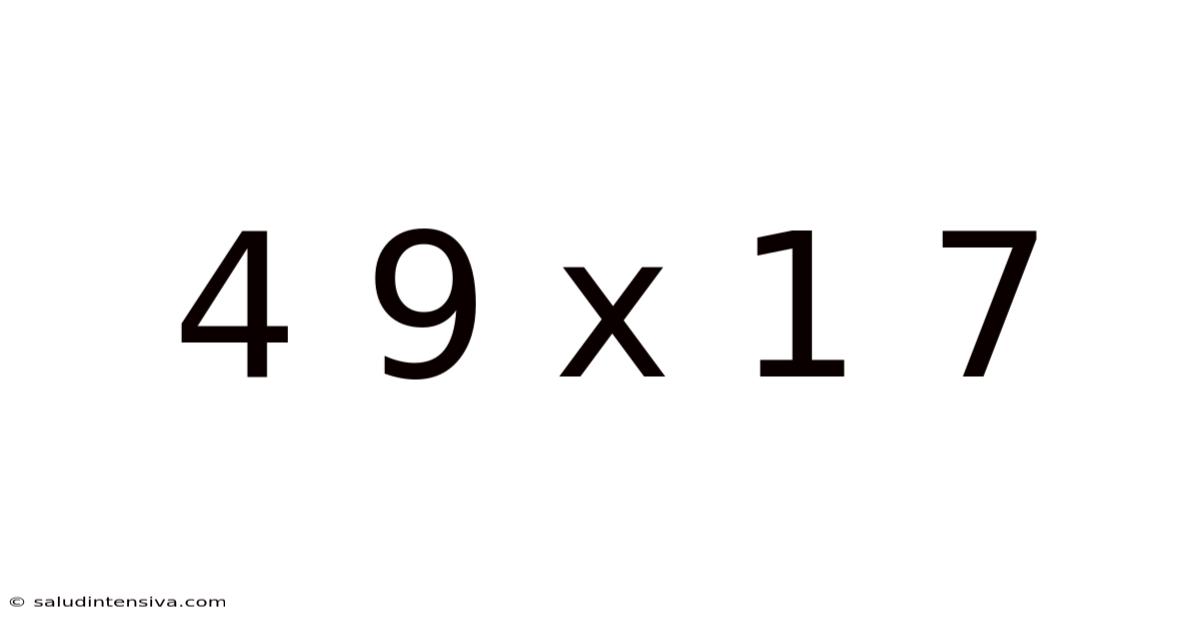
Table of Contents
Unlocking the Mystery of 49 x 17: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem 49 x 17, delving beyond the basic answer to uncover the underlying mathematical principles, alternative calculation methods, and real-world applications. Understanding this seemingly straightforward calculation provides a strong foundation for more complex mathematical concepts. We'll cover various techniques, from the standard algorithm to mental math tricks, making this a comprehensive guide for students of all levels.
The Standard Algorithm: A Step-by-Step Approach
The most common method for solving 49 x 17 is the standard multiplication algorithm, taught in most elementary schools. This method involves breaking down the problem into smaller, more manageable parts.
-
Step 1: Multiply 49 by 7 (the units digit of 17).
49 x 7 = 343. Write down 343.
-
Step 2: Multiply 49 by 10 (the tens digit of 17).
49 x 10 = 490. Write this below 343, aligning the units digit with the tens digit of 343.
-
Step 3: Add the two results together.
343 + 490 = 833
Therefore, 49 x 17 = 833.
This method provides a systematic approach, making it easy to follow and minimizes errors. However, it's not always the fastest or most intuitive method, especially for larger numbers.
Alternative Calculation Methods: Expanding Your Mathematical Toolkit
While the standard algorithm is reliable, exploring alternative methods enhances mathematical understanding and problem-solving skills. Here are a few alternatives to consider:
1. Distributive Property: This method leverages the distributive property of multiplication over addition (or subtraction). We can break down 17 into 10 + 7, then multiply each part by 49 and add the results.
- 49 x (10 + 7) = (49 x 10) + (49 x 7) = 490 + 343 = 833
This method highlights the underlying principles of multiplication and can be easier to visualize.
2. Foil Method (Similar to Distributive Property, but visually different): While primarily used for binomials in algebra, the concept can be applied here. Think of 49 as (50 - 1) and 17 as it is. Then:
- (50 - 1) x 17 = (50 x 17) - (1 x 17) = 850 - 17 = 833
This approach uses easier-to-handle numbers (multiples of 10) and subtraction, making mental calculations more manageable.
3. Lattice Multiplication: This visual method is particularly useful for larger numbers. It involves creating a grid and performing single-digit multiplications within each cell. The results are then added diagonally. While more visually complex for 49 x 17, it's a valuable technique for understanding the multiplication process and a great tool to teach younger children.
4. Mental Math Techniques: With practice, you can perform this calculation mentally using a variety of techniques. One approach involves rounding and adjusting:
- Round 49 to 50: 50 x 17 = 850. Since we rounded up by 1, subtract 17 (17 x 1): 850 - 17 = 833
This approach requires estimation skills and familiarity with multiplication tables.
The Importance of Understanding the Underlying Principles
Beyond simply obtaining the answer (833), understanding the underlying mathematical principles is crucial. This problem touches upon several key concepts:
-
Place Value: The standard algorithm hinges on understanding place value (units, tens, hundreds). Incorrect placement of digits leads to incorrect answers.
-
Distributive Property: As shown above, this property is fundamental to multiplication and simplifies complex calculations. It's a cornerstone of algebraic manipulation.
-
Commutative Property: While not directly used in the calculation itself, the commutative property (a x b = b x a) highlights that the order of multiplication doesn't affect the result. This understanding helps to streamline calculations and choose the most efficient approach.
-
Associative Property: Similarly, the associative property ((a x b) x c = a x (b x c)) isn't directly applied here but offers insights into grouping numbers for easier calculation.
Real-World Applications: Beyond the Textbook
While 49 x 17 might seem abstract, understanding multiplication has countless real-world applications:
-
Shopping: Calculating the total cost of multiple items, especially with discounts or bulk purchases.
-
Cooking/Baking: Scaling recipes up or down, adjusting ingredient quantities.
-
Construction/Engineering: Calculating material needs, determining dimensions, and calculating costs.
-
Finance: Calculating interest, determining loan payments, managing budgets.
-
Data Analysis: Working with datasets, calculating averages, and performing statistical calculations.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to learn different methods of multiplication? A: Learning multiple methods provides a deeper understanding of the underlying mathematical principles and improves problem-solving skills. It also allows for flexibility in choosing the most efficient method for a particular problem.
-
Q: What if I make a mistake during the standard algorithm? A: Double-check your work carefully, paying close attention to the placement of digits and the addition steps. Using alternative methods can help verify your answer.
-
Q: Are there any online resources or tools to help with multiplication practice? A: While we can't provide links here, a simple online search for "multiplication practice" will yield numerous websites and apps designed to help students improve their multiplication skills.
-
Q: How can I improve my mental math skills for multiplication? A: Regular practice is key. Start with smaller numbers and gradually work your way up to larger numbers. Focus on mastering multiplication tables and learning mental math techniques.
Conclusion: Mastering Multiplication, One Problem at a Time
The seemingly simple problem of 49 x 17 offers a window into the rich world of mathematics. Beyond the answer, understanding the various methods of calculation and the underlying mathematical principles empowers you with versatile problem-solving skills applicable in numerous contexts. By exploring different approaches and practicing regularly, you can not only master multiplication but also develop a deeper appreciation for the elegance and power of mathematical concepts. This journey of understanding multiplication extends far beyond the immediate answer, shaping your ability to approach complex problems with confidence and ingenuity. Remember, the key to mathematical proficiency lies not only in memorization but also in a deep grasp of the underlying principles and the development of versatile problem-solving strategies.
Latest Posts
Latest Posts
-
What Is 1 In Fraction
Sep 15, 2025
-
Future Value Of One Table
Sep 15, 2025
-
Lowest Term Of 2 3
Sep 15, 2025
-
Convert 300 Lbs To Kgs
Sep 15, 2025
-
Surface Area Of Cuboid Calculator
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 4 9 X 1 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.