4 Divided By 4 3
saludintensiva
Sep 23, 2025 · 6 min read
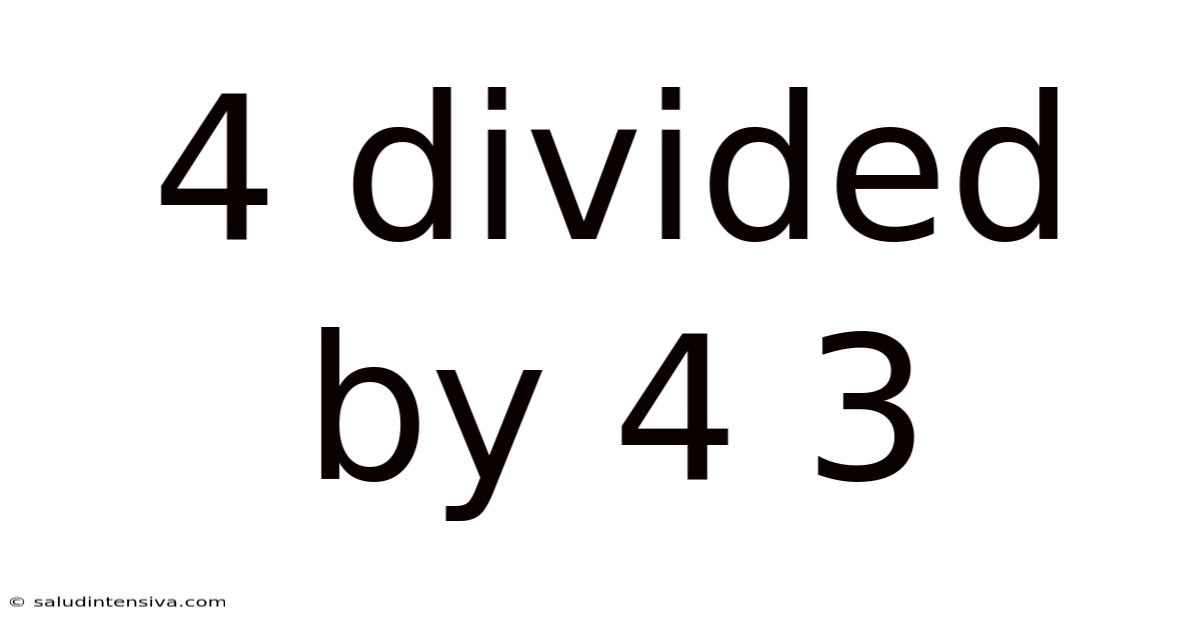
Table of Contents
Decoding 4 Divided by 4 3: A Deep Dive into Mathematical Operations
This article explores the seemingly simple yet conceptually rich problem of "4 divided by 4 3". We'll unpack the meaning behind this expression, delve into the order of operations (often remembered by the acronym PEMDAS/BODMAS), and explore the different interpretations and potential solutions. Understanding this seemingly simple problem provides a strong foundation for more complex mathematical concepts. We'll also address frequently asked questions and provide clarifying examples to ensure a thorough understanding.
Understanding the Problem: 4 ÷ 4 3
At first glance, the expression "4 divided by 4 3" might seem straightforward. However, the absence of explicit grouping symbols (parentheses, brackets, or braces) introduces ambiguity. This ambiguity highlights the critical importance of order of operations in mathematics. Without a clear understanding of the order of operations, we can arrive at different, and incorrect, answers.
The Order of Operations: PEMDAS/BODMAS
The order of operations dictates the sequence in which mathematical operations should be performed to ensure a consistent and unambiguous result. This is crucial when dealing with expressions containing multiple operations. Two common acronyms are used to represent the order of operations:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- BODMAS: Brackets, Orders (powers and roots), Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Both PEMDAS and BODMAS represent the same fundamental principles; the only difference lies in the terminology used for parentheses/brackets and exponents/orders.
Interpreting and Solving 4 ÷ 4 3 using PEMDAS/BODMAS
Let's apply the order of operations to solve "4 divided by 4 3". Since there are no parentheses or exponents, we proceed directly to multiplication and division, working from left to right.
-
Multiplication/Division (from left to right): The expression can be interpreted as 4 ÷ (4 x 3). Following the order of operations, we first perform the multiplication: 4 x 3 = 12.
-
Division: Now we have 4 ÷ 12. Performing the division, we get 4 ÷ 12 = 1/3 or 0.333...
Therefore, using the standard order of operations, the solution to "4 divided by 4 3" is 1/3 or approximately 0.333...
Alternative Interpretations and Potential Errors
The absence of parentheses leads to the possibility of misinterpretations. Someone might mistakenly interpret the expression as (4 ÷ 4) x 3. Let's analyze this:
-
Division: (4 ÷ 4) = 1
-
Multiplication: 1 x 3 = 3
This yields a result of 3, which is incorrect according to the standard order of operations. This example emphasizes the vital role of parentheses in clarifying the intended order of operations. If the intention was to perform the division before the multiplication, parentheses would be necessary. For instance, (4 ÷ 4) x 3 would be correctly interpreted as 3.
Expanding the Concept: Incorporating More Complex Operations
Let's consider a slightly more complex example to further illustrate the importance of order of operations:
12 ÷ 2 + 4 x 3 – 6
Following PEMDAS/BODMAS:
-
Division: 12 ÷ 2 = 6
-
Multiplication: 4 x 3 = 12
-
Addition: 6 + 12 = 18
-
Subtraction: 18 – 6 = 12
Therefore, the solution to 12 ÷ 2 + 4 x 3 – 6 is 12. This example demonstrates how adhering to the correct order ensures a consistent and accurate solution. Any deviation from the prescribed order can lead to incorrect answers.
The Role of Parentheses: Clarifying Ambiguity
Parentheses play a crucial role in removing ambiguity and directing the order of operations. Let's revisit our original problem, incorporating parentheses to showcase different interpretations:
-
(4 ÷ 4) x 3 = 3: This expression explicitly states that the division should be performed before the multiplication.
-
4 ÷ (4 x 3) = 1/3: This expression clearly indicates that the multiplication should be done before the division, which aligns with the standard order of operations interpretation when parentheses are absent.
The use of parentheses eliminates any potential confusion and ensures that the intended calculation is performed correctly. It is a vital tool for accurately representing complex mathematical expressions.
Practical Applications: Real-World Scenarios
The order of operations is not just a theoretical concept; it has practical applications in various fields:
-
Computer Programming: Programming languages strictly adhere to the order of operations to ensure accurate execution of code. Incorrect ordering can lead to program errors.
-
Engineering and Physics: Calculations in engineering and physics frequently involve multiple operations. Following the correct order is essential for accurate results and safe designs.
-
Finance and Accounting: Financial calculations, such as calculating compound interest or analyzing investment returns, require precise adherence to the order of operations.
-
Data Analysis and Statistics: Statistical calculations and data analysis often involve complex formulas and expressions, where the correct order of operations is crucial for accurate conclusions.
Frequently Asked Questions (FAQ)
Q1: Why is the order of operations important?
A1: The order of operations ensures that mathematical expressions are interpreted consistently. Without a set order, different people might interpret the same expression differently, leading to various, incorrect results. The consistent order ensures everyone arrives at the same correct answer.
Q2: What happens if I don't follow the order of operations?
A2: Not following the order of operations will generally lead to incorrect results. The answer you obtain will be different from the mathematically correct solution.
Q3: Can I change the order of operations?
A3: No, the order of operations is a fundamental principle in mathematics. Changing the order will inevitably lead to incorrect calculations. Parentheses can be used to override the default order, but they don't change the fundamental principles.
Q4: Are there any exceptions to the order of operations?
A4: No, there are no exceptions to the standard order of operations (PEMDAS/BODMAS). Any perceived exceptions are usually due to misinterpretations or missing parentheses.
Q5: How can I improve my understanding of the order of operations?
A5: Practice is key. Work through various examples, including those with multiple operations and parentheses. Familiarize yourself with different types of problems to strengthen your understanding. Online resources and educational materials can also be helpful in clarifying any remaining doubts.
Conclusion: Mastering the Fundamentals
Understanding the order of operations, as demonstrated by solving "4 divided by 4 3," is a fundamental skill in mathematics. It ensures consistent and accurate calculations, which is crucial across various disciplines. The absence of parentheses highlights the importance of adhering to PEMDAS/BODMAS to avoid ambiguity and obtain the correct answer. By mastering this foundational concept, you lay a strong groundwork for tackling more complex mathematical problems and applications in the future. Remember that the key to success lies in consistent application of the rules and the strategic use of parentheses to clarify complex expressions.
Latest Posts
Latest Posts
-
How To Determine Pool Volume
Sep 23, 2025
-
Whats 20 Percent Of 1200
Sep 23, 2025
-
Convert 6 5 Cm To Inches
Sep 23, 2025
-
Convert 24 Centimeters To Inches
Sep 23, 2025
-
Grams Per Gallon Of Water
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 4 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.