4 Divided By Negative 2
saludintensiva
Sep 17, 2025 · 6 min read
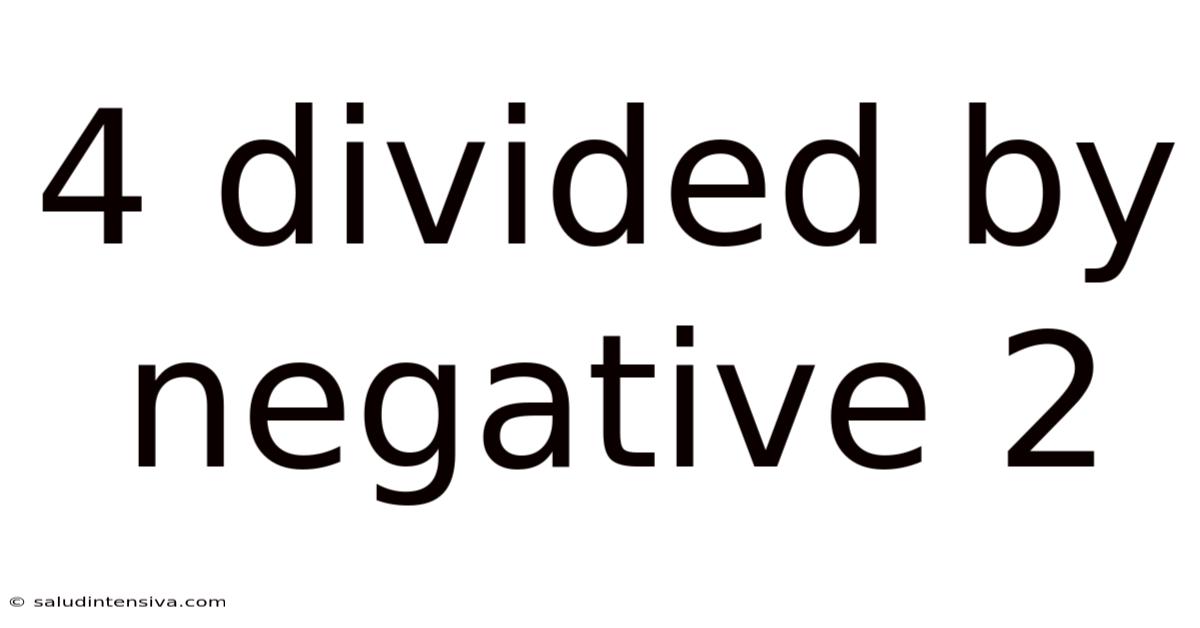
Table of Contents
Diving Deep into 4 Divided by -2: Understanding Division with Negative Numbers
Understanding division, especially when negative numbers are involved, is a fundamental concept in mathematics. This comprehensive guide will explore the seemingly simple problem of 4 divided by -2, delving into the underlying principles, providing step-by-step explanations, and addressing common misconceptions. We'll cover the rules of signs, different approaches to solving the problem, and explore the broader implications of this operation within the context of algebra and real-world applications. By the end, you'll not only know the answer but also possess a solid understanding of division with negative numbers.
Understanding the Basics of Division
Before tackling the specific problem of 4 divided by -2, let's refresh our understanding of division itself. Division is essentially the inverse operation of multiplication. When we say 4 divided by 2, we're asking: "What number, when multiplied by 2, gives us 4?" The answer, of course, is 2. We can express this mathematically as:
4 ÷ 2 = 2 or 4 / 2 = 2
This simple example illustrates the core concept: division determines how many times one number (the divisor) is contained within another number (the dividend).
Introducing Negative Numbers
Negative numbers represent values less than zero. They are often used to represent quantities like debt, temperature below zero, or a decrease in value. Understanding how to perform arithmetic operations with negative numbers is crucial for mastering basic algebra and more advanced mathematical concepts.
The Rules of Signs in Division
The key to solving 4 divided by -2 lies in understanding the rules of signs when dealing with division (and multiplication) involving negative numbers. These rules are:
- Positive ÷ Positive = Positive: A positive number divided by a positive number always results in a positive number.
- Negative ÷ Negative = Positive: A negative number divided by a negative number also results in a positive number.
- Positive ÷ Negative = Negative: A positive number divided by a negative number results in a negative number.
- Negative ÷ Positive = Negative: A negative number divided by a positive number results in a negative number.
These rules can be summarized as: If the signs of the dividend and divisor are the same, the result is positive. If the signs are different, the result is negative.
Solving 4 Divided by -2
Now, let's apply these rules to our problem: 4 divided by -2.
Following the rules above, we identify that we have a positive dividend (4) and a negative divisor (-2). Since the signs are different, the result will be negative. The absolute value of the division is:
4 ÷ 2 = 2
Therefore, combining the magnitude and the sign, we get:
4 ÷ (-2) = -2
Multiple Approaches to Solving the Problem
While the rules of signs provide a quick and efficient method, let's explore other approaches to reinforce our understanding:
-
Using the Number Line: Visualizing the problem on a number line can be helpful. Start at 0. Since we're dividing by -2, we're essentially asking how many groups of -2 are in 4. If we move two units to the left (-2) twice, we reach -4. To reach 4, we have to consider the direction. Moving to the right from -4 to 0 and then to 4 necessitates a negative sign, thus indicating that we have -2 such groups.
-
Relationship with Multiplication: Remember, division is the inverse of multiplication. Therefore, we can check our answer by multiplying the quotient (-2) by the divisor (-2). If the result equals the dividend (4), then our answer is correct.
(-2) x (-2) = 4. This confirms that our answer, -2, is correct.
- Using Fractions: We can represent the division as a fraction: 4 / -2. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This gives us -2/1, which simplifies to -2.
The Importance of Understanding Signs
The correct application of the rules of signs is crucial, not just for this specific problem, but for all mathematical operations involving negative numbers. Mistakes in handling signs can lead to incorrect results, and it's essential to be comfortable with these fundamental principles. Understanding the reasoning behind these rules helps prevent careless errors.
Real-World Applications
Division involving negative numbers appears in many real-world scenarios:
-
Finance: Calculating losses or debts. For example, if a company loses $4 million over two years, the average yearly loss is calculated as 4,000,000 / -2 = -2,000,000. The negative sign indicates a loss.
-
Temperature: Calculating average temperature change. If the temperature drops 4 degrees over two hours, the average hourly drop is 4 / -2 = -2 degrees.
-
Physics: Representing vectors and velocity. Negative values indicate opposite directions.
Expanding the Concept: Algebra and Beyond
The principles discussed here extend far beyond simple arithmetic. Understanding division with negative numbers is foundational to more advanced mathematical concepts like:
-
Algebra: Solving equations and inequalities involving negative numbers is crucial for algebra. Being comfortable with the rules of signs enables accurate manipulation of variables and equations.
-
Calculus: Limits and derivatives often involve operations with negative numbers, requiring a solid understanding of these basic rules.
-
Linear Algebra: Matrices and vectors commonly use negative numbers, making a strong grasp of the principles of negative number operations essential.
Frequently Asked Questions (FAQ)
Q: What if I divide -4 by 2?
A: Using the rules of signs, a negative dividend (-4) divided by a positive divisor (2) results in a negative quotient. Therefore, -4 / 2 = -2.
Q: Is there a difference between 4 / -2 and -4 / 2?
A: No, both expressions are equivalent and result in -2. The order doesn't change the outcome.
Q: Why is a negative divided by a negative positive?
A: This is a fundamental rule of mathematics. It can be explained through repeated subtraction or by considering the concept of multiplicative inverses. The product of two negative numbers is positive, and division is the inverse of multiplication.
Q: Can I use a calculator to solve this?
A: Yes, most calculators will correctly handle division with negative numbers. However, understanding the underlying principles is essential for problem-solving beyond simple calculations.
Conclusion
The seemingly simple problem of 4 divided by -2 offers a gateway to a deeper understanding of negative numbers and the fundamental rules of arithmetic. By mastering the rules of signs and understanding the various approaches to solving this type of problem, you build a strong foundation for success in more advanced mathematical concepts. Remember, the answer is -2, but the true value lies in the understanding of why it is -2. This knowledge will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Meters Per Second To Rpm
Sep 17, 2025
-
Gcf Of 18 And 50
Sep 17, 2025
-
First 10 Multiples Of 7
Sep 17, 2025
-
How Long Is 280 Minutes
Sep 17, 2025
-
Multiples Of 6 To 100
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By Negative 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.