4 Is What Of 20
saludintensiva
Sep 24, 2025 · 5 min read
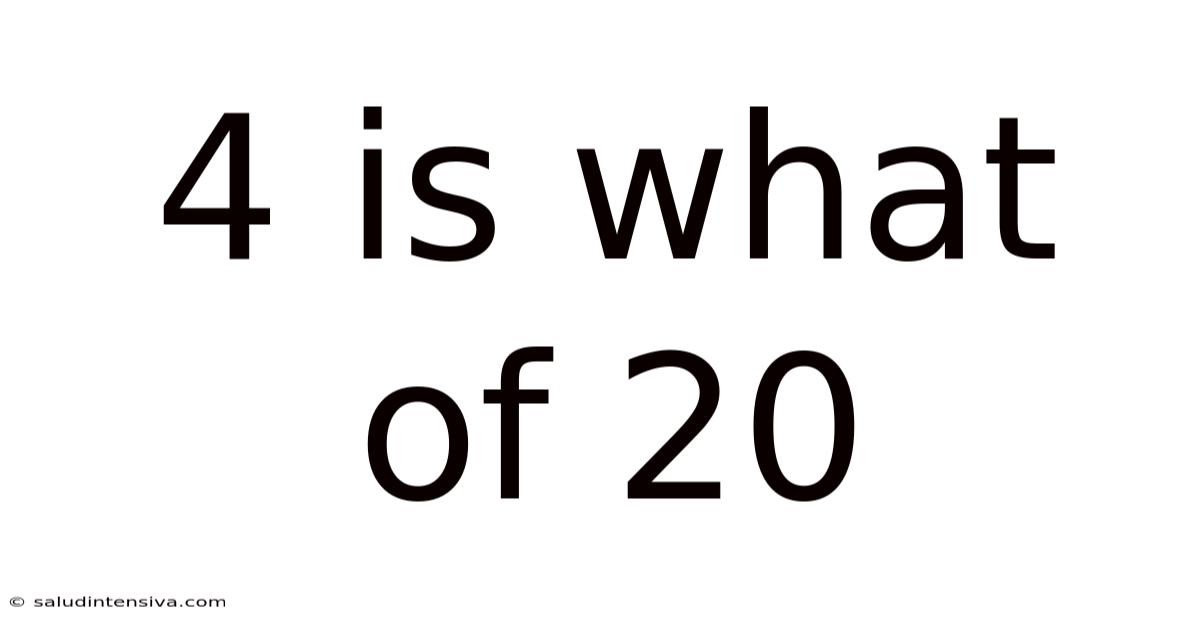
Table of Contents
4 is What Percent of 20? Understanding Percentages and Their Applications
This article will delve into the seemingly simple question: "4 is what percent of 20?" While the answer might seem immediately obvious to some, understanding the underlying principles of percentages and their diverse applications is crucial for various aspects of life, from everyday finances to advanced scientific calculations. We'll explore not only the solution to this specific problem but also the broader context of percentage calculations, including different methods of solving them and real-world examples.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). So, when we say "x%," we mean x out of every 100. This representation is incredibly useful for comparing proportions, making data easier to understand, and performing various calculations.
For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Similarly, 10% represents 10 out of 100, or 1/10, or 0.1.
Calculating Percentages: Three Key Methods
There are several ways to calculate percentages, each offering a slightly different approach depending on the context and your familiarity with mathematical concepts. Let's explore three common methods:
Method 1: Using the Fraction Method
This is arguably the most intuitive method, especially for beginners. To find what percent 4 is of 20, we first express the relationship as a fraction:
4/20
Next, we simplify this fraction to its lowest terms:
4/20 = 1/5
Now, to express this fraction as a percentage, we need to convert it to a fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 20:
(1/5) * (20/20) = 20/100
Therefore, 4 is 20% of 20.
Method 2: Using the Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100. Starting with the fraction 4/20:
4/20 = 0.2
Multiplying the decimal by 100 gives us the percentage:
0.2 * 100 = 20%
This method is efficient and particularly useful when working with calculators.
Method 3: Using the Proportion Method
This method sets up a proportion to solve for the unknown percentage. We can represent the problem as:
4/20 = x/100
To solve for x (the percentage), we cross-multiply:
20x = 400
Then, divide both sides by 20:
x = 20
Therefore, 4 is 20% of 20. This method highlights the proportional relationship between the parts and the whole.
Solving Variations of the Problem
The core concept of percentages allows us to adapt the solution to various related problems. For example:
-
What is 20% of 20? This involves multiplying 20 by 0.20 (which is the decimal equivalent of 20%), resulting in 4.
-
20 is what percent of 40? This mirrors the original problem; using any of the methods above, you'll find that 20 is 50% of 40.
-
4 is 20% of what number? This problem requires a slightly different approach. Let's call the unknown number "y". We can set up the equation:
0.20y = 4
Solving for y:
y = 4 / 0.20 = 20
Therefore, 4 is 20% of 20.
These variations demonstrate the flexibility and adaptability of percentage calculations.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in everyday life. Understanding them is essential for:
-
Finance: Calculating interest rates, discounts, taxes, tips, and investment returns. For example, a 10% discount on a $100 item saves you $10.
-
Statistics: Analyzing data, interpreting survey results, and understanding probabilities. For instance, if 60% of respondents prefer a certain product, this indicates a strong preference.
-
Science: Expressing concentrations of solutions, measuring experimental error, and reporting data. A 5% saline solution, for instance, contains 5 grams of salt per 100 milliliters of solution.
-
Retail: Calculating markups, discounts, and profit margins. Understanding percentage changes in sales figures is crucial for business decisions.
-
Everyday Life: Calculating the percentage of a task completed, understanding nutritional information on food labels (e.g., percentage of daily value), and interpreting various forms of data presented as percentages.
Frequently Asked Questions (FAQ)
Q1: What is the easiest method to calculate percentages?
A1: The easiest method often depends on individual preference and the specific problem. For simple calculations, the fraction method can be intuitive. For more complex problems or when using a calculator, the decimal method is often more efficient.
Q2: Can I use a calculator to calculate percentages?
A2: Yes, most calculators have a percentage function (%) that simplifies the calculation. However, understanding the underlying principles is still crucial for interpreting the results and solving problems without a calculator.
Q3: What if I have a percentage and need to find the original value?
A3: This involves working backward from the percentage. You would typically divide the given value by the percentage (expressed as a decimal) to find the original value.
Q4: Are there any online tools or calculators to help with percentage calculations?
A4: Yes, many online tools and calculators are available to assist with percentage calculations. However, developing a solid understanding of the underlying concepts is key to confidently handling these calculations in any context.
Q5: How can I improve my understanding of percentages?
A5: Practice is key. Try working through various examples, starting with simple problems and gradually increasing the complexity. Understanding the different methods and applying them to real-world scenarios will significantly enhance your understanding and skill.
Conclusion
The question "4 is what percent of 20?" serves as a gateway to understanding the broader world of percentage calculations. While the answer is a straightforward 20%, the process of arriving at this answer, and the various methods involved, highlights the fundamental importance of percentages in various fields. Mastering percentage calculations isn't just about solving mathematical problems; it's about gaining a valuable skill applicable to numerous aspects of daily life, from personal finance to professional endeavors. By understanding the concepts and practicing different methods, you can confidently tackle percentage calculations and apply this knowledge to improve your decision-making abilities in various contexts. Remember, the more you practice, the more comfortable and proficient you will become with percentages and their numerous applications.
Latest Posts
Latest Posts
-
Sq Cm To Sq Ft
Sep 24, 2025
-
1 3 Yard To Feet
Sep 24, 2025
-
1 Hour 15 Min Timer
Sep 24, 2025
-
Cost Per Square Foot Concrete
Sep 24, 2025
-
1 1000 As A Percent
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.