40 32 As A Percentage
saludintensiva
Sep 22, 2025 · 5 min read
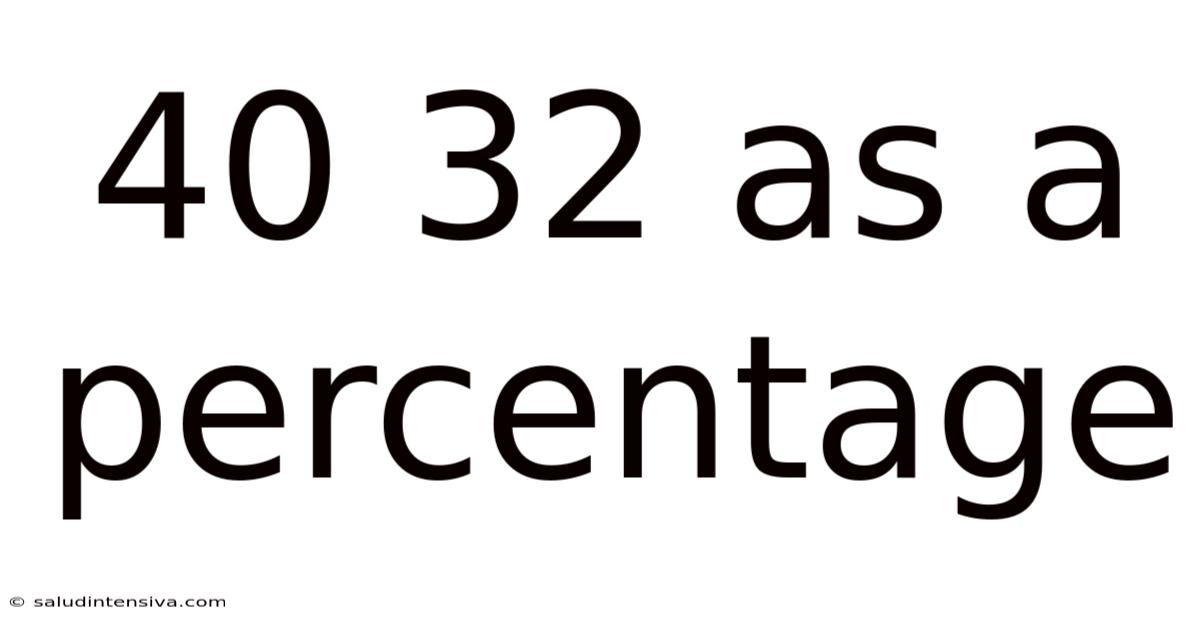
Table of Contents
Understanding 40 out of 32 as a Percentage: A Comprehensive Guide
Finding a percentage when the numerator (the top number) is larger than the denominator (the bottom number) might seem unusual at first. This article will guide you through understanding how to calculate 40 out of 32 as a percentage, explain the underlying mathematical principles, and explore practical applications. We'll also address common misconceptions and frequently asked questions. Understanding this concept is crucial for various fields, from basic math to advanced statistics and even everyday scenarios involving proportions and ratios.
Introduction: What Does "Percentage" Mean?
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" ( per centum in Latin). We use percentages to represent proportions, often comparing parts to a whole. For example, scoring 80% on a test means you answered 80 out of 100 questions correctly. In the case of 40 out of 32, we're dealing with a situation where the 'part' is larger than the 'whole'. This doesn't invalidate the concept; rather, it indicates a value greater than 100%.
Calculating 40 out of 32 as a Percentage: Step-by-Step Guide
The calculation process involves two primary steps:
-
Forming a fraction: Represent the problem as a fraction: 40/32. This means 40 represents the part, and 32 represents the whole.
-
Converting the fraction to a decimal: Divide the numerator (40) by the denominator (32): 40 ÷ 32 = 1.25
-
Converting the decimal to a percentage: Multiply the decimal by 100%: 1.25 x 100% = 125%
Therefore, 40 out of 32 is 125%. This result signifies that 40 is 125% of 32. It's more than 32 because the part is larger than the whole.
Understanding the Concept of Percentages Greater Than 100%
It's essential to grasp that percentages aren't limited to values between 0% and 100%. Percentages greater than 100% simply indicate that the part is larger than the whole. This scenario is common in various contexts:
-
Growth and Increase: If a company's sales increase from 32 units to 40 units, the percentage increase is 125%. This showcases substantial growth exceeding the initial value.
-
Overachievement: If a salesperson's target was 32 sales, but they achieved 40, they exceeded their target by 125%.
-
Financial Analysis: In financial reports, percentages exceeding 100% often represent increases in profit, revenue, or assets.
-
Statistical Analysis: In data analysis, values greater than 100% can appear when comparing changes over time or comparing different groups.
Practical Applications of Percentages Greater Than 100%
The ability to calculate and interpret percentages greater than 100% is essential in several real-world scenarios:
-
Business and Finance: Tracking sales growth, profit margins, return on investment (ROI), and comparing financial performance across different periods.
-
Economics: Analyzing economic growth rates, inflation rates, and changes in economic indicators.
-
Science: Expressing experimental results, such as increased yields in agricultural experiments or enhanced efficiency in industrial processes.
-
Education: Calculating percentage increases in student enrollment or test scores.
-
Everyday Life: Determining percentage increases in wages, prices, or costs.
Mathematical Explanation: Ratio and Proportion
The concept of 40 out of 32 as a percentage is fundamentally based on the principles of ratio and proportion. A ratio is a comparison between two quantities. In this case, the ratio is 40:32. A proportion establishes an equivalence between two ratios. We can express the ratio 40:32 as a proportion:
40/32 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
32x = 4000
x = 4000/32 = 125
Therefore, x = 125%, confirming our earlier calculation. This demonstrates the mathematical foundation supporting the percentage calculation.
Avoiding Common Mistakes in Percentage Calculations
Several common errors can occur when dealing with percentage calculations, especially when the part is larger than the whole:
-
Incorrectly identifying the whole: Ensuring the correct identification of the 'whole' is crucial. In our example, 32 is the whole, not 40.
-
Division errors: Carefully perform the division (numerator divided by denominator). A simple calculation mistake can lead to an incorrect result.
-
Incorrect conversion to percentage: After obtaining the decimal, remember to multiply by 100% to express the value as a percentage.
-
Misinterpreting percentages greater than 100%: Understand that values exceeding 100% represent a proportion where the part is greater than the whole.
Frequently Asked Questions (FAQ)
-
Q: Can a percentage be greater than 100%?
- A: Yes, absolutely! Percentages greater than 100% simply indicate that the part is larger than the whole.
-
Q: How do I calculate a percentage decrease if the new value is smaller than the original value?
- A: You would still use the same basic formula: (New Value - Original Value) / Original Value * 100%. The result will be a negative percentage, indicating a decrease.
-
Q: What if I have a percentage and need to find the original value?
- A: You can use algebraic manipulation. For instance, if 125% of a value is 40, you can set up the equation: 1.25x = 40, and solve for x (the original value).
-
Q: Are there any online calculators to verify my percentage calculations?
- A: Many online calculators are available that can help you verify your percentage calculations, providing an extra layer of accuracy.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, particularly those exceeding 100%, is a valuable skill applicable across diverse fields. This article has provided a comprehensive guide, breaking down the steps, clarifying the underlying mathematical concepts, and addressing common questions. By mastering this skill, you can effectively analyze data, interpret results, and make informed decisions in various aspects of your life, from personal finance to professional endeavors. Remember that accuracy and a clear understanding of the principles are key to successfully working with percentages. Practice is crucial to build proficiency and confidence in handling percentage calculations.
Latest Posts
Latest Posts
-
What Number Has 19 Zeros
Sep 22, 2025
-
Division Using An Area Model
Sep 22, 2025
-
73 Cm Convert To Inches
Sep 22, 2025
-
Cubit Is How Many Feet
Sep 22, 2025
-
What Numbers Multply Make 24
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 40 32 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.