4th Square Root Of 81
saludintensiva
Sep 10, 2025 · 6 min read
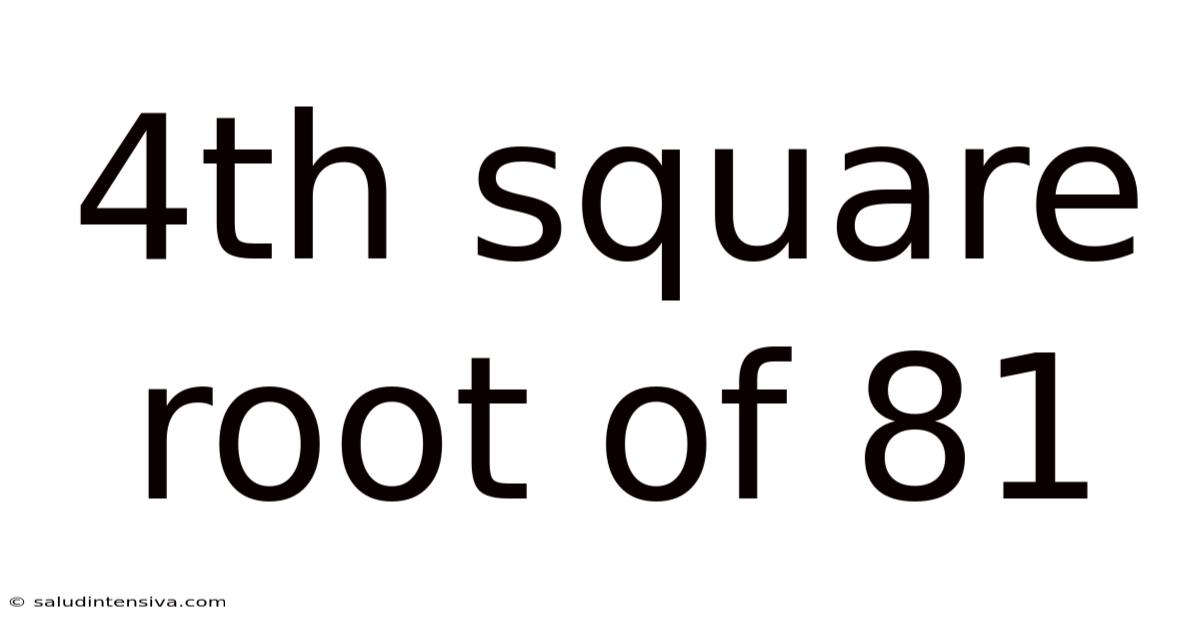
Table of Contents
Unveiling the Secrets of the Fourth Root of 81: A Deep Dive into Radical Expressions
Finding the fourth root of 81 might seem like a simple mathematical task, a quick calculation for those familiar with exponents and radicals. However, delving deeper reveals a wealth of mathematical concepts and connections that extend far beyond a single numerical answer. This article will not only provide the solution but also explore the underlying principles, explore different methods of solving the problem, and examine the broader implications within the realm of mathematics. We'll unravel the mystery behind the fourth root of 81, clarifying its meaning and significance.
Understanding Roots and Exponents: A Foundation
Before we tackle the fourth root of 81, let's solidify our understanding of fundamental mathematical concepts. The term "root" is intrinsically linked to exponents. When we say "the nth root of a number x", we're essentially asking: "What number, when multiplied by itself n times, equals x?" This is represented mathematically as:
x<sup>(1/n)</sup> = <sup>n</sup>√x
In simpler terms, the nth root is the inverse operation of raising a number to the power of n. For example:
- 2<sup>2</sup> = 4 (2 squared equals 4)
- √4 = 2 (The square root of 4 is 2)
The fourth root of 81, denoted as <sup>4</sup>√81, asks: "What number, when multiplied by itself four times, equals 81?"
Calculating the Fourth Root of 81: Different Approaches
There are several ways to approach calculating the fourth root of 81. Let's explore a few:
1. Prime Factorization:
This method involves breaking down 81 into its prime factors. Prime factorization is a fundamental technique in number theory, allowing us to express a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's factorize 81:
81 = 9 x 9 = 3 x 3 x 3 x 3 = 3<sup>4</sup>
Since 81 can be expressed as 3 raised to the power of 4 (3<sup>4</sup>), its fourth root is simply 3. This is because 3 x 3 x 3 x 3 = 81.
2. Using Exponents:
Remember the relationship between roots and exponents: <sup>n</sup>√x = x<sup>(1/n)</sup>. We can apply this directly to our problem:
<sup>4</sup>√81 = 81<sup>(1/4)</sup>
Since 81 = 3<sup>4</sup>, we can substitute:
(3<sup>4</sup>)<sup>(1/4)</sup>
Using the power of a power rule [(a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>], we get:
3<sup>(4 x 1/4)</sup> = 3<sup>1</sup> = 3
Therefore, the fourth root of 81 is 3.
3. Trial and Error (Less Efficient, but Illustrative):
While less efficient for larger numbers, trial and error can be a helpful approach for understanding the concept. We can start by testing small numbers:
- 1 x 1 x 1 x 1 = 1
- 2 x 2 x 2 x 2 = 16
- 3 x 3 x 3 x 3 = 81
We find that 3 multiplied by itself four times equals 81.
Beyond the Numerical Answer: Exploring Complex Numbers
While the fourth root of 81 is 3 in the realm of real numbers, the mathematical landscape expands considerably when we introduce complex numbers. A complex number has a real part and an imaginary part, with the imaginary unit i defined as the square root of -1 (i = √-1).
In the realm of complex numbers, every non-zero number has n distinct nth roots. For the fourth root of 81, this means there are four distinct solutions, not just 3. To find these, we use Euler's formula and polar coordinates.
The complex number z can be written in polar form as z = r(cos θ + i sin θ), where r is the magnitude and θ is the argument. For 81, the magnitude r = 81 and the principal argument θ = 0.
The four fourth roots are given by:
z<sub>k</sub> = 81<sup>(1/4)</sup> [cos((0 + 2πk)/4) + i sin((0 + 2πk)/4)] where k = 0, 1, 2, 3.
This yields the following four roots:
- z<sub>0</sub> = 3 (the real root we've already found)
- z<sub>1</sub> = 3i
- z<sub>2</sub> = -3
- z<sub>3</sub> = -3i
These four roots are equally spaced around a circle in the complex plane, centered at the origin, with a radius of 3. This illustrates the richness and complexity that unfolds when we extend our calculations beyond the realm of real numbers.
Applications of Fourth Roots and Radical Expressions
The concept of roots, particularly fourth roots, has wide-ranging applications across various fields:
-
Engineering and Physics: Calculations involving oscillations, wave mechanics, and alternating current often require working with fourth roots and other radical expressions.
-
Computer Graphics and Game Development: Rendering realistic 3D models and animations relies heavily on mathematical computations, including various types of roots, for transformations and manipulations.
-
Finance and Economics: Calculating compound interest or determining the present value of future investments often involves exponential and radical equations.
-
Statistics and Probability: Many statistical distributions and formulas incorporate radicals in their calculations.
-
Cryptography: Cryptography employs advanced mathematical techniques, including those involving roots and exponents, to secure data and communications.
Frequently Asked Questions (FAQs)
Q1: Is there only one fourth root of 81?
A1: In the realm of real numbers, yes, there's only one: 3. However, in the realm of complex numbers, there are four distinct fourth roots, as explained in the previous section.
Q2: How can I calculate the fourth root of other numbers?
A2: The methods outlined above—prime factorization and using exponents—can be applied to other numbers. For larger numbers, a calculator or computer software can be very helpful. For complex numbers, more advanced mathematical techniques are required.
Q3: What is the difference between a square root and a fourth root?
A3: A square root (√x) asks: "What number, when multiplied by itself, equals x?" A fourth root (<sup>4</sup>√x) asks: "What number, when multiplied by itself four times, equals x?" The key difference lies in the number of times the root must be multiplied by itself to reach the original number.
Q4: Are there other types of roots besides square and fourth roots?
A4: Yes, there are cube roots (<sup>3</sup>√x), fifth roots (<sup>5</sup>√x), and so on. The concept of roots extends to any positive integer n.
Q5: Why is understanding roots important?
A5: Understanding roots is crucial for a solid foundation in algebra, calculus, and many other areas of mathematics and science. They are essential building blocks for solving complex equations and understanding various mathematical concepts and their applications in the real world.
Conclusion: Beyond the Basics of the Fourth Root of 81
This exploration of the fourth root of 81 has shown that even seemingly simple mathematical problems can lead to deeper insights. We've moved from a basic calculation to a deeper understanding of exponents, roots, prime factorization, and the fascinating world of complex numbers. The journey to understanding the fourth root of 81 has highlighted the interconnectedness of different mathematical concepts and showcased the broad applicability of these principles across various disciplines. It’s not just about finding the answer; it's about understanding the why behind the answer and appreciating the underlying mathematical elegance. Remember, the pursuit of mathematical knowledge is a continuous journey of discovery, and each step forward reveals new layers of understanding and appreciation for the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Excel Convert Time To Number
Sep 10, 2025
-
Fractions Equal To 5 8
Sep 10, 2025
-
What Is 75 In Celsius
Sep 10, 2025
-
8 1 2 As A Decimal
Sep 10, 2025
-
7 10 As A Percentage
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 4th Square Root Of 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.