5 2/6 - 2 5/6
saludintensiva
Sep 15, 2025 · 6 min read
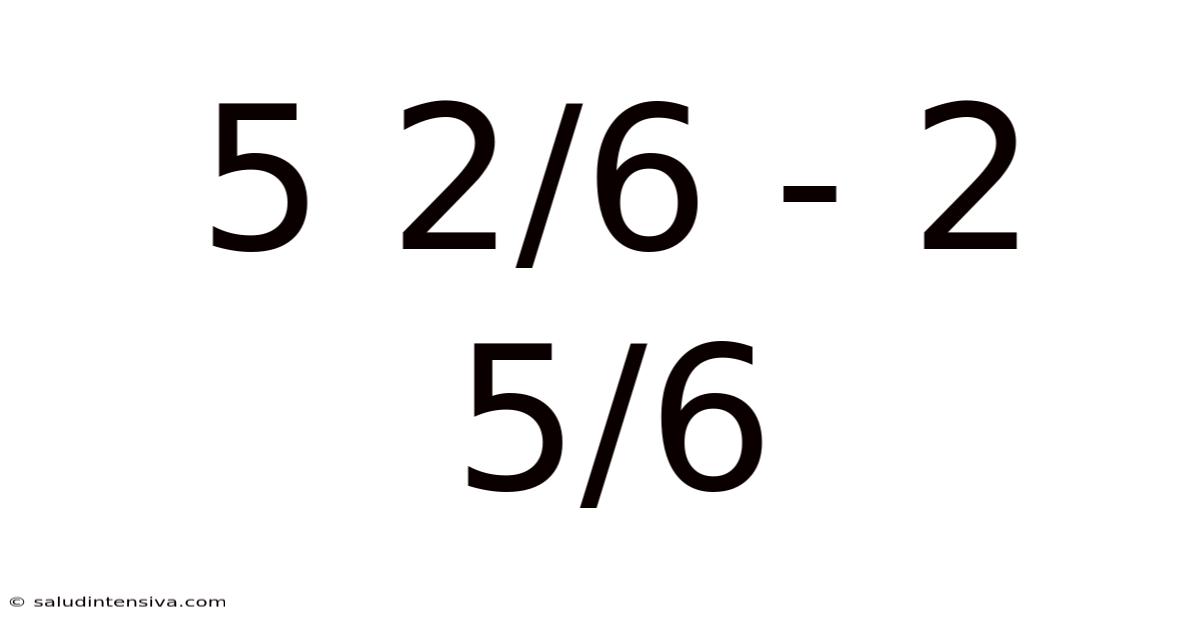
Table of Contents
Subtracting Mixed Numbers: A Deep Dive into 5 2/6 - 2 5/6
This article provides a comprehensive guide to solving the subtraction problem 5 2/6 - 2 5/6. We'll explore the steps involved, delve into the underlying mathematical principles, and address common misconceptions. By the end, you'll not only understand how to solve this specific problem but also gain the confidence to tackle any mixed number subtraction with ease. This guide is perfect for students, educators, and anyone looking to brush up on their fraction skills.
Understanding Mixed Numbers
Before tackling the subtraction, let's refresh our understanding of mixed numbers. A mixed number combines a whole number and a fraction. For example, 5 2/6 represents 5 whole units and 2/6 of another unit. Understanding this representation is crucial for accurately performing operations like subtraction.
Step-by-Step Solution: 5 2/6 - 2 5/6
The immediate challenge in this subtraction is that the fraction in the subtrahend (2 5/6) is larger than the fraction in the minuend (5 2/6). This requires a crucial step that many students find tricky: borrowing from the whole number.
1. Borrowing from the Whole Number:
Since we can't directly subtract 5/6 from 2/6, we need to borrow one whole unit from the 5. This borrowed unit is then converted into a fraction with the same denominator as the existing fractions (6 in this case). One whole unit is equivalent to 6/6.
Therefore, we rewrite 5 2/6 as:
5 2/6 = 4 + 1 + 2/6 = 4 + 6/6 + 2/6 = 4 8/6
Now our subtraction problem becomes:
4 8/6 - 2 5/6
2. Subtracting the Fractions:
Now we can subtract the fractions independently:
8/6 - 5/6 = 3/6
3. Subtracting the Whole Numbers:
Next, we subtract the whole numbers:
4 - 2 = 2
4. Combining the Results:
Finally, we combine the results from the fraction and whole number subtraction:
2 + 3/6 = 2 3/6
5. Simplifying the Fraction:
The fraction 3/6 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 3.
3/6 = 1/2
Therefore, the final answer is:
2 1/2
A Deeper Look: The Mathematical Principles
The process of borrowing highlights a fundamental concept in arithmetic: the flexibility of number representation. We can represent the same quantity in different ways (e.g., 5 2/6 and 4 8/6). This flexibility is crucial when performing operations where direct subtraction isn't immediately possible. The borrowing process essentially transforms the problem into an equivalent but more manageable form.
Alternative Approach: Converting to Improper Fractions
Another method to solve this problem involves converting both mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
1. Converting to Improper Fractions:
-
5 2/6: To convert this, multiply the whole number (5) by the denominator (6), add the numerator (2), and place the result over the denominator: (5 * 6) + 2 = 32/6
-
2 5/6: Similarly, (2 * 6) + 5 = 17/6
The subtraction problem now becomes:
32/6 - 17/6
2. Subtracting the Improper Fractions:
Since the denominators are the same, we simply subtract the numerators:
32/6 - 17/6 = 15/6
3. Simplifying and Converting Back to a Mixed Number:
The fraction 15/6 can be simplified by dividing both numerator and denominator by their greatest common divisor (3):
15/6 = 5/2
Finally, we convert the improper fraction 5/2 back to a mixed number by dividing the numerator (5) by the denominator (2):
5 ÷ 2 = 2 with a remainder of 1. This gives us 2 1/2.
Both methods—borrowing and converting to improper fractions—yield the same correct answer: 2 1/2. Choosing the method that feels most comfortable and intuitive is key to mastering mixed number subtraction.
Common Mistakes and How to Avoid Them
Many students struggle with mixed number subtraction due to a few common errors:
-
Forgetting to Borrow: This is the most frequent mistake. Remember to borrow a whole unit if the fraction in the subtrahend is larger than the fraction in the minuend.
-
Incorrect Borrowing: Ensure you correctly convert the borrowed whole unit into a fraction with the same denominator. A common error is to incorrectly add the borrowed unit to the numerator without adjusting the denominator.
-
Ignoring Fraction Simplification: Always simplify the resulting fraction to its lowest terms. This presents the answer in its most concise and mathematically correct form.
Frequently Asked Questions (FAQs)
Q: Can I solve this problem using decimals?
A: Yes, you can. First convert both mixed numbers into decimals: 5 2/6 ≈ 5.333 and 2 5/6 ≈ 2.833. Then, subtract: 5.333 - 2.833 = 2.5. This decimal 2.5 is equivalent to the fraction 2 1/2. However, working directly with fractions often provides a deeper understanding of the underlying mathematical principles.
Q: What if the denominators are different?
A: If the denominators are different, you'll need to find a common denominator before you can subtract the fractions. This involves finding the least common multiple (LCM) of the denominators. For example, if you were subtracting 3 1/2 from 5 1/3, you would first find a common denominator (6) and then rewrite the fractions as 3 3/6 and 5 2/6 before proceeding with the subtraction.
Q: Are there other ways to check my answer?
A: You can use estimation to check your answer's reasonableness. For example, 5 2/6 is approximately 5 and 2 5/6 is approximately 3. The difference between 5 and 3 is 2, which is close to our answer of 2 1/2. Another approach involves using the improper fraction method and then converting back to check your simplification process.
Q: What resources are available for further practice?
A: Numerous online resources, textbooks, and educational websites offer practice problems and explanations on mixed number subtraction. Focus on working through problems systematically, understanding each step, and checking your work.
Conclusion
Subtracting mixed numbers, as demonstrated through the problem 5 2/6 - 2 5/6, requires a solid understanding of fraction manipulation and the ability to borrow from whole numbers. By mastering the techniques explained in this article, you can confidently tackle a wide range of fraction problems. Remember to practice regularly, utilize different approaches, and always check your answers to solidify your understanding and build your mathematical skills. The ability to work comfortably with fractions forms a crucial foundation for more advanced mathematical concepts. Don't hesitate to review this guide and practice the techniques shown to reinforce your comprehension. The key to success lies in consistent practice and a thorough understanding of the underlying principles.
Latest Posts
Latest Posts
-
19 3 As A Decimal
Sep 15, 2025
-
Present Value Of 1 Table
Sep 15, 2025
-
Ratios Equivalent To 3 6
Sep 15, 2025
-
Improper Fraction For 4 1 2
Sep 15, 2025
-
9 16 In Decimal Form
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 2/6 - 2 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.