5 25 As A Decimal
saludintensiva
Sep 11, 2025 · 5 min read
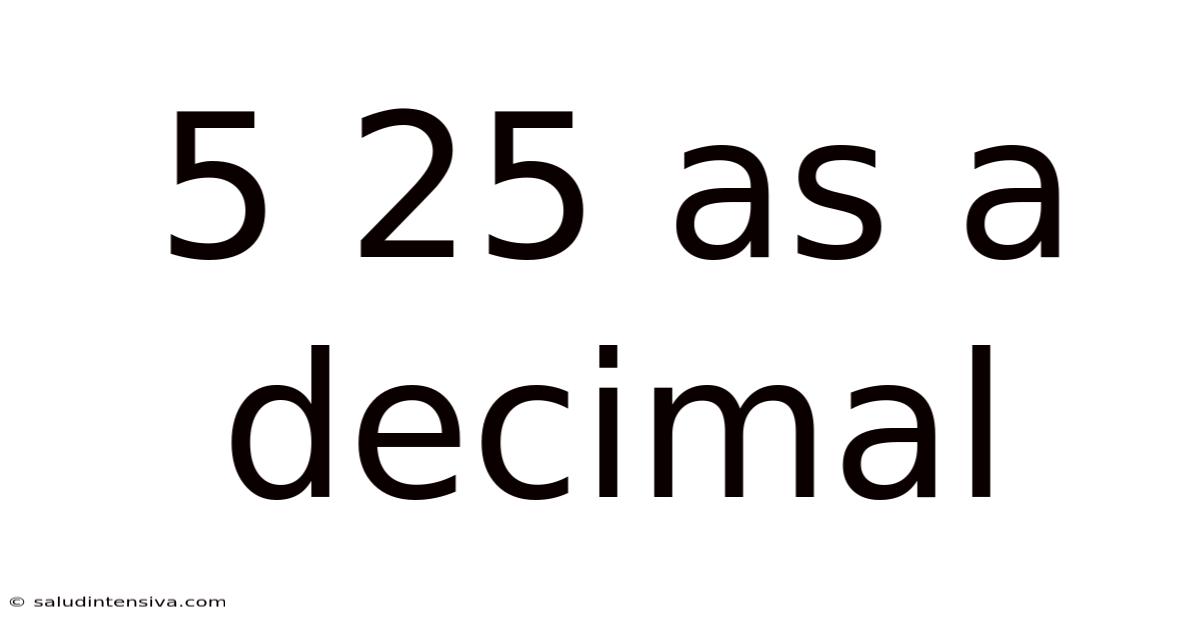
Table of Contents
5/25 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article will delve deep into converting the fraction 5/25 into its decimal form, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll also address common misconceptions and answer frequently asked questions, ensuring a thorough grasp of this seemingly simple yet crucial concept. This guide is designed for students, educators, and anyone looking to solidify their understanding of fraction-to-decimal conversion.
Introduction: Understanding Fractions and Decimals
Before we tackle the conversion of 5/25, let's briefly review the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole.
A decimal, on the other hand, represents a number using a base-ten system. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a decreasing power of ten (tenths, hundredths, thousandths, and so on).
Converting a fraction to a decimal involves finding the equivalent decimal representation of the fraction. This is often done through division.
Method 1: Simplifying the Fraction
The simplest method to convert 5/25 to a decimal involves simplifying the fraction first. We look for a common factor between the numerator (5) and the denominator (25). In this case, both 5 and 25 are divisible by 5.
- Simplification: 5/25 = (5 ÷ 5) / (25 ÷ 5) = 1/5
Now, we have a simplified fraction, 1/5. This makes the division process much easier.
Method 2: Direct Division
This method involves directly dividing the numerator by the denominator. We can use long division or a calculator to perform this operation.
-
Long Division: To perform long division, we divide 5 by 25. Since 5 is smaller than 25, we add a decimal point and a zero to the dividend (5 becomes 5.0). Then, we perform the division:
25 goes into 50 twice (2 x 25 = 50). Therefore, 5/25 = 0.2
-
Calculator: Using a calculator, simply enter 5 ÷ 25, which will directly give you the answer: 0.2
Method 3: Converting to a Percentage and then to a Decimal
Another approach involves converting the fraction to a percentage first and then to a decimal.
-
Convert to Percentage: To convert a fraction to a percentage, we multiply the fraction by 100%:
(5/25) x 100% = 20%
-
Convert Percentage to Decimal: To convert a percentage to a decimal, we divide the percentage by 100:
20% ÷ 100 = 0.2
Understanding the Result: 0.2
The decimal equivalent of 5/25 is 0.2. This means that 5/25 represents two-tenths of a whole. It's important to understand that this decimal represents the same value as the fraction; it's simply expressed in a different format.
The Significance of Decimal Representation
The decimal representation of fractions is crucial for various reasons:
- Ease of Comparison: Comparing decimals is often simpler than comparing fractions, especially when the fractions have different denominators.
- Calculations: Performing arithmetic operations (addition, subtraction, multiplication, and division) with decimals is generally easier than with fractions.
- Real-World Applications: Decimals are widely used in various real-world applications, including finance, engineering, science, and everyday measurements.
Common Misconceptions
A common misconception is that converting a fraction to a decimal always results in a terminating decimal (a decimal that ends). While this is true for fractions with denominators that are factors of powers of 10 (like 2, 5, 10, 20, 25, etc.), it's not true for all fractions. Fractions with denominators that are not factors of powers of 10 will result in repeating decimals (decimals with a pattern that repeats infinitely).
Further Exploration: Working with More Complex Fractions
The principles discussed above can be extended to convert more complex fractions to decimals. For example, if you encounter a fraction like 17/25, you would follow the same steps: simplify if possible, then divide the numerator by the denominator. The result would be 0.68.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to convert 5/25 to a decimal?
A: The easiest way is to simplify the fraction to 1/5 and then divide 1 by 5, which equals 0.2. Alternatively, you can directly divide 5 by 25 using a calculator or long division.
Q: Can all fractions be converted to terminating decimals?
A: No, only fractions whose denominators are composed solely of factors of 2 and 5 can be converted to terminating decimals. Other fractions result in repeating or non-terminating decimals.
Q: Why is it important to learn how to convert fractions to decimals?
A: Converting fractions to decimals is a fundamental skill in mathematics, with applications across various fields. Decimals are often easier to work with in calculations and comparisons.
Q: What if the fraction is a mixed number (e.g., 2 1/4)?
A: To convert a mixed number to a decimal, first convert the mixed number into an improper fraction. For example, 2 1/4 becomes 9/4. Then, divide the numerator (9) by the denominator (4). The result would be 2.25.
Q: Are there any online tools that can help with fraction-to-decimal conversions?
A: Yes, numerous online calculators and converters can assist with fraction-to-decimal conversions. However, understanding the underlying principles is crucial for developing a solid mathematical foundation.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 5/25 to its decimal equivalent (0.2) is a straightforward process that illustrates the fundamental relationship between fractions and decimals. Mastering this conversion, along with understanding the underlying principles, is crucial for success in mathematics and its numerous applications. Through simplifying the fraction, direct division, or converting to a percentage, you can confidently navigate this essential mathematical concept. Remember to practice different methods to solidify your understanding and build confidence in tackling more complex fraction-to-decimal conversions.
Latest Posts
Latest Posts
-
What Time Is 14 37
Sep 11, 2025
-
Equivalent Fraction For 3 10
Sep 11, 2025
-
Round To The Nearest Year
Sep 11, 2025
-
Price Per Kg To Lb
Sep 11, 2025
-
Gcf Of Two Monomials Calculator
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 5 25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.