5 5/8 As A Decimal
saludintensiva
Sep 14, 2025 · 5 min read
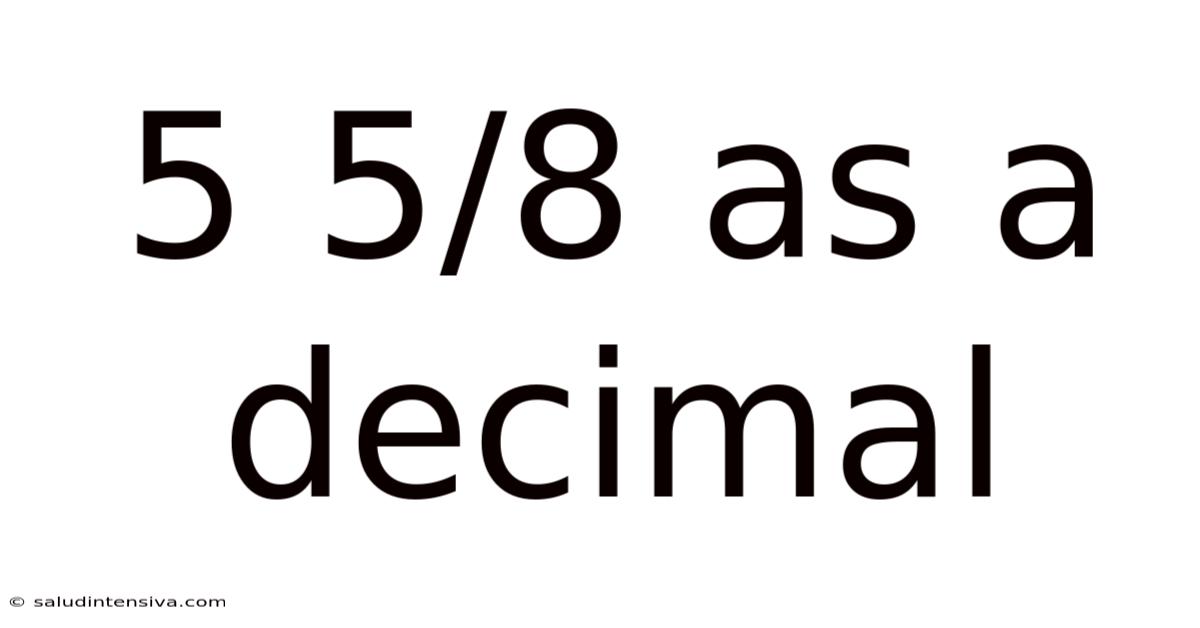
Table of Contents
Understanding 5 5/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields, from everyday calculations to advanced scientific computations. This comprehensive guide delves into the process of converting the mixed number 5 5/8 into its decimal equivalent. We'll explore the underlying principles, provide step-by-step instructions, and address common queries, ensuring a thorough understanding of this essential concept. This article will cover different methods, providing you with a versatile approach to tackling similar fraction-to-decimal conversions. Understanding this process will bolster your confidence in tackling more complex mathematical problems.
Understanding Mixed Numbers and Fractions
Before we begin, let's clarify the terms. A mixed number, like 5 5/8, combines a whole number (5 in this case) and a fraction (5/8). A fraction represents a part of a whole, with the top number (numerator) indicating the number of parts and the bottom number (denominator) indicating the total number of parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal Directly
This method involves directly converting the fractional part of the mixed number into a decimal and then adding the whole number.
Step 1: Divide the numerator by the denominator
To convert the fraction 5/8 to a decimal, we perform the division: 5 ÷ 8 = 0.625
Step 2: Add the whole number
Now, add the whole number part of the mixed number to the decimal equivalent of the fraction: 5 + 0.625 = 5.625
Therefore, 5 5/8 as a decimal is 5.625
This is the simplest and most direct approach. However, understanding other methods enhances your mathematical flexibility and provides alternative solutions for more complex fractions.
Method 2: Converting the Mixed Number to an Improper Fraction First
This method involves initially transforming the mixed number into an improper fraction before converting it into a decimal. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Step 1: Convert the mixed number to an improper fraction
To convert 5 5/8 to an improper fraction, we multiply the whole number (5) by the denominator (8) and add the numerator (5). This result becomes the new numerator, while the denominator remains the same.
(5 x 8) + 5 = 45
So, 5 5/8 becomes 45/8.
Step 2: Divide the numerator by the denominator
Now, divide the numerator (45) by the denominator (8): 45 ÷ 8 = 5.625
Therefore, 5 5/8 as a decimal is 5.625
This method demonstrates a different pathway to the same result, highlighting the interconnectedness of different mathematical representations. This is especially useful when dealing with more complex mixed numbers or when performing further calculations involving fractions.
Method 3: Using Decimal Equivalents of Common Fractions
This method leverages the memorization of common fraction-decimal equivalents to expedite the conversion process. While this method might seem limited at first, knowing common equivalents makes quick mental calculations possible.
Many students memorize the decimal equivalents of fractions with denominators like 2, 4, 8, 10, and so on. Knowing that 1/8 = 0.125, you can quickly calculate 5/8 as 5 * 0.125 = 0.625. Then, add the whole number 5 to get 5.625.
This method, while requiring prior knowledge of common fraction-decimal equivalents, showcases the power of memorization and pattern recognition in efficient mathematical problem-solving. It’s a valuable tool for quick mental calculations.
The Significance of Decimal Representation
Understanding how to convert fractions to decimals is crucial for several reasons:
-
Real-world applications: Many practical calculations, especially those involving measurements, money, or scientific data, use decimals. Converting fractions to decimals allows for easier comparison and computation.
-
Enhanced precision: Decimals offer greater precision than fractions in many scenarios, especially when dealing with small increments.
-
Compatibility with calculators and computers: Calculators and computers primarily work with decimal numbers, making this conversion necessary for utilizing these tools in solving mathematical problems.
-
Building mathematical fluency: Mastering this conversion strengthens your overall mathematical foundation, preparing you for more advanced concepts.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to terminating decimals?
A1: No, not all fractions can be converted to terminating decimals. Fractions with denominators that can be expressed as 2<sup>m</sup> * 5<sup>n</sup> (where 'm' and 'n' are non-negative integers) result in terminating decimals. Fractions with denominators containing prime factors other than 2 and 5 will result in repeating decimals.
Q2: What is a repeating decimal?
A2: A repeating decimal is a decimal that has a digit or sequence of digits that repeat infinitely. For example, 1/3 = 0.3333... where the '3' repeats endlessly. These are often represented with a bar over the repeating sequence (e.g., 0.3̅).
Q3: How do I convert a fraction with a repeating decimal to a fraction?
A3: Converting repeating decimals to fractions requires algebraic manipulation. It involves setting the decimal equal to 'x', multiplying by a power of 10 to align the repeating part, subtracting the original equation, and then solving for 'x'. This is a more advanced topic but essential for a comprehensive understanding of decimal-fraction relationships.
Q4: Are there any other methods to convert fractions to decimals?
A4: Yes, there are. One method involves using long division, which is a more manual approach suitable for understanding the underlying process. However, for efficiency, especially with more complex fractions, calculators are often preferred.
Q5: Why is understanding this conversion important beyond school?
A5: This conversion skill is essential in various professions, including engineering, finance, accounting, and even cooking and construction, where precise measurements are crucial. The ability to accurately convert fractions to decimals ensures accuracy and precision in real-world applications.
Conclusion
Converting 5 5/8 to its decimal equivalent, 5.625, involves a straightforward process that can be approached through different methods. Understanding these various methods, not only provides you with a solid understanding of the core concept but also equips you with adaptable skills for handling more complex fraction-to-decimal conversions. The significance of this skill extends far beyond the classroom, making it an invaluable tool for navigating the numerical demands of everyday life and various professional pursuits. The mastery of this seemingly simple conversion represents a significant step towards a stronger foundation in mathematics and a greater appreciation of the interconnectedness of mathematical concepts. Remember to practice regularly to solidify your understanding and build your confidence in tackling similar problems.
Latest Posts
Latest Posts
-
What Are Multiples Of 54
Sep 14, 2025
-
15 Out Of 25 Percentage
Sep 14, 2025
-
Square Root Of 16 9
Sep 14, 2025
-
Is 4 8 Equivalent To 3 6
Sep 14, 2025
-
What Time Is 20 39
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5 5/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.