5 7 Divided By 5
saludintensiva
Sep 23, 2025 · 5 min read
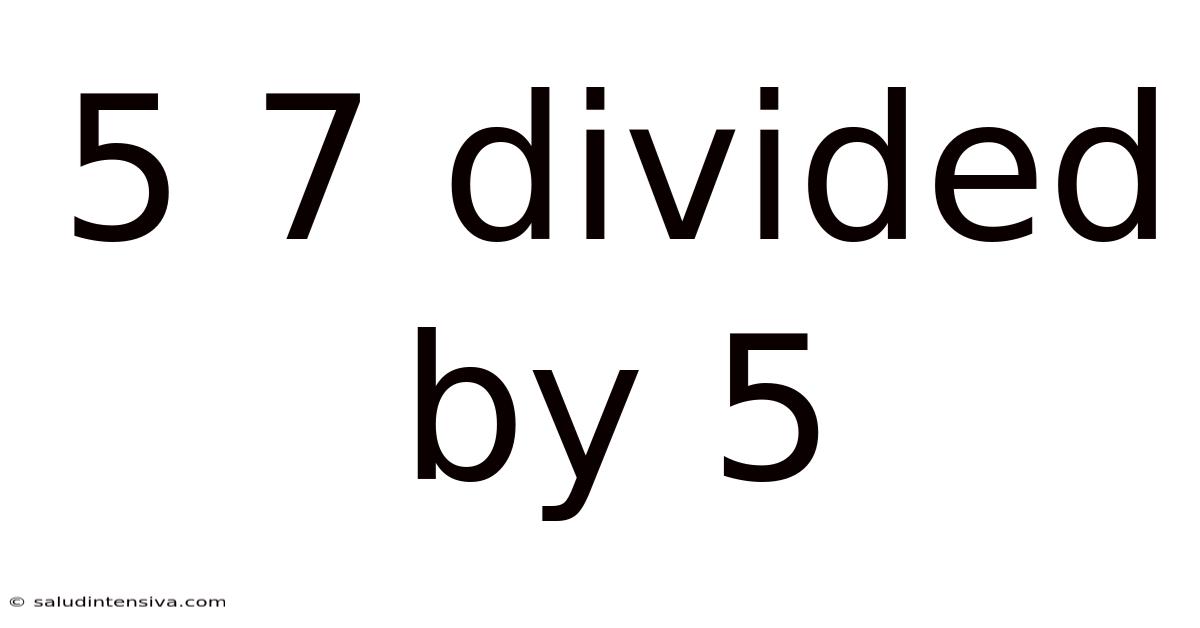
Table of Contents
Unraveling the Mystery: 57 Divided by 5
This article delves into the seemingly simple yet surprisingly multifaceted problem of dividing 57 by 5. While the basic arithmetic might seem straightforward, exploring this calculation opens doors to understanding fundamental mathematical concepts, including division, remainders, decimals, and their practical applications. We’ll break down the process step-by-step, explore different methods of solving it, and even delve into the theoretical implications. This comprehensive guide aims to not just provide the answer but to equip you with a deeper understanding of division and its significance.
Understanding the Basics of Division
Before we tackle 57 divided by 5, let's refresh our understanding of division. Division is essentially the process of splitting a quantity into equal parts. In the expression "a ÷ b," 'a' is the dividend (the number being divided), 'b' is the divisor (the number we're dividing by), and the result is the quotient. Sometimes, division doesn't result in a whole number; this leaves a remainder.
For example, if we divide 10 by 2 (10 ÷ 2), the quotient is 5 because 2 goes into 10 five times evenly. However, if we divide 11 by 2 (11 ÷ 2), the quotient is 5, and there's a remainder of 1. This is because 2 goes into 11 five times with one left over.
Method 1: Long Division
Long division is a traditional method for solving division problems, especially those involving larger numbers. Here’s how to solve 57 ÷ 5 using long division:
-
Set up the problem: Write 57 inside the long division symbol (⟌) and 5 outside.
-
Divide: Ask yourself, "How many times does 5 go into 5?" The answer is 1. Write the '1' above the '5' in 57.
-
Multiply: Multiply the quotient (1) by the divisor (5). 1 x 5 = 5. Write '5' below the '5' in 57.
-
Subtract: Subtract 5 from 5. 5 - 5 = 0.
-
Bring down: Bring down the next digit from the dividend (7).
-
Divide again: Ask, "How many times does 5 go into 7?" The answer is 1 (with a remainder). Write the '1' above the '7'.
-
Multiply again: Multiply the quotient (1) by the divisor (5). 1 x 5 = 5. Write '5' below the '7'.
-
Subtract again: Subtract 5 from 7. 7 - 5 = 2. This is your remainder.
Therefore, 57 ÷ 5 = 11 with a remainder of 2. We can express this as 11 R2.
Method 2: Repeated Subtraction
Another approach is repeated subtraction. We repeatedly subtract the divisor (5) from the dividend (57) until we reach a number less than the divisor. Let’s see how this works:
- 57 - 5 = 52
- 52 - 5 = 47
- 47 - 5 = 42
- 42 - 5 = 37
- 37 - 5 = 32
- 32 - 5 = 27
- 27 - 5 = 22
- 22 - 5 = 17
- 17 - 5 = 12
- 12 - 5 = 7
- 7 - 5 = 2
We subtracted 5 eleven times before reaching a number (2) less than 5. This confirms that 57 ÷ 5 is 11 with a remainder of 2.
Method 3: Converting to a Decimal
While the remainder is useful in some contexts, we can also express the result as a decimal. To do this, we continue the division process beyond the whole number quotient:
-
After obtaining the quotient 11 and the remainder 2, add a decimal point to the dividend (57) and append a zero (making it 57.0).
-
Bring down the zero. Now we have 20.
-
Ask, "How many times does 5 go into 20?" The answer is 4.
-
Multiply 4 x 5 = 20.
-
Subtract 20 - 20 = 0.
Therefore, 57 ÷ 5 = 11.4.
Understanding Remainders and Decimals
The remainder (2 in this case) represents the portion of the dividend that wasn't fully divisible by the divisor. Converting to a decimal provides a more precise representation of the division, indicating that each of the five parts is 11.4 units. The choice between using a remainder or a decimal depends on the context of the problem. For example, if we're dividing 57 candies among 5 friends, each friend gets 11 candies, and there are 2 candies left over. But if we're dealing with measurements or monetary values, a decimal representation might be more appropriate.
Real-World Applications
The ability to perform division, including understanding remainders and decimals, is crucial in various real-world scenarios:
- Sharing equally: Dividing resources (candies, toys, money) among a group of people.
- Calculating averages: Determining the average score on a test, average speed, or average temperature.
- Measuring and scaling: Converting units (e.g., inches to centimeters), scaling recipes, or calculating distances.
- Financial calculations: Dividing expenses among roommates, calculating unit costs, or determining profit margins.
- Programming and data analysis: Division is a fundamental operation in computer programming and data analysis for tasks like array manipulation, data normalization, and algorithm development.
Frequently Asked Questions (FAQs)
-
Q: What is the best method for dividing 57 by 5?
- A: The best method depends on your preference and the context. Long division is a systematic approach suitable for all cases. Repeated subtraction is useful for illustrating the concept of division, and converting to a decimal provides a precise numerical result.
-
Q: What if I get a recurring decimal?
- A: Some divisions result in recurring or repeating decimals (e.g., 1/3 = 0.333...). These are handled differently based on the context. In some cases, rounding off to a suitable number of decimal places is sufficient.
-
Q: Can a remainder be larger than the divisor?
- A: No. If the remainder is larger than the divisor, it indicates an error in the division process. The divisor should go into the remainder at least once.
-
Q: Why is understanding remainders important?
- A: Remainders show the leftover portion after dividing as evenly as possible. In real-world problems, they represent what's left unallocated or incomplete.
Conclusion: Beyond the Numbers
Dividing 57 by 5, seemingly a trivial arithmetic problem, offers a gateway to understanding the broader principles of division, remainders, and decimals. Mastering these concepts extends beyond simple calculations; they form the foundation for tackling more complex mathematical problems and real-world applications. Whether you use long division, repeated subtraction, or convert to a decimal, the crucial takeaway is not just the numerical answer but the deeper understanding of the process and its significance. Remember that mathematics isn't just about finding answers; it's about understanding the why behind the what. This comprehensive exploration of 57 divided by 5 underscores this very principle.
Latest Posts
Latest Posts
-
650 Sq Feet In Meters
Sep 23, 2025
-
19 Celsius Converted To Fahrenheit
Sep 23, 2025
-
Heartbeat For Girl Vs Boy
Sep 23, 2025
-
How To Figure Linear Footage
Sep 23, 2025
-
76 Acres To Sq Ft
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 7 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.