5 Squared Plus 12 Squared
saludintensiva
Sep 17, 2025 · 5 min read
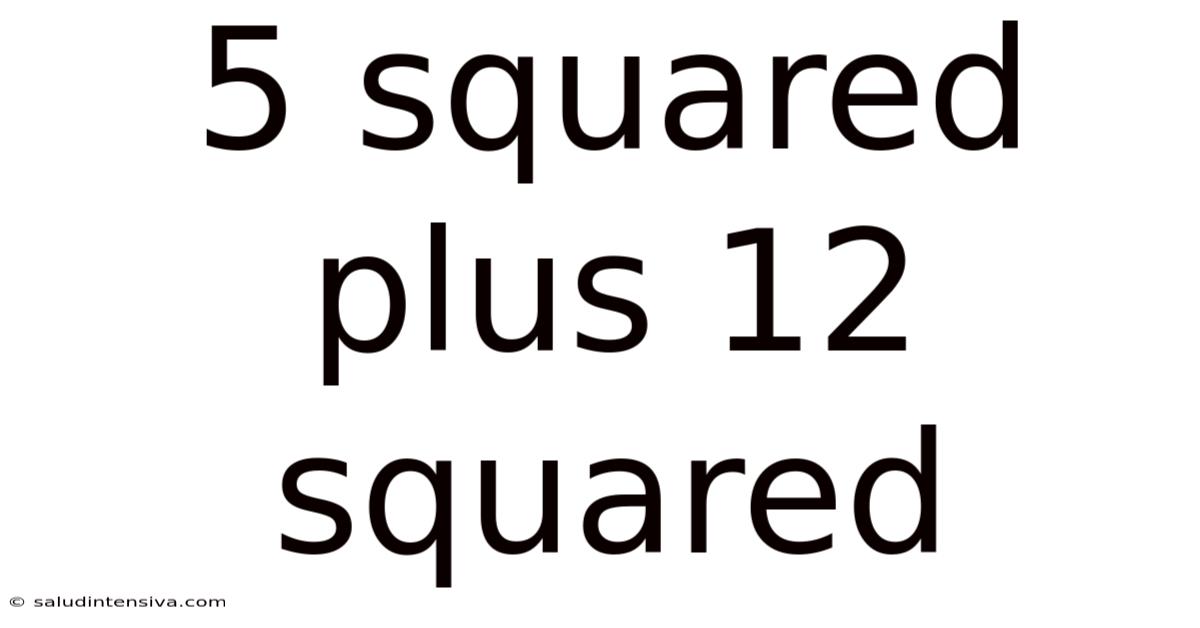
Table of Contents
Unveiling the Mystery: 5 Squared Plus 12 Squared and its Implications
The seemingly simple mathematical expression "5 squared plus 12 squared" (5² + 12²) might appear innocuous at first glance. However, this expression opens doors to a fascinating exploration of fundamental mathematical concepts, including the Pythagorean theorem, Euclidean geometry, and even the deeper connections between algebra and geometry. This article will delve into the calculation, its significance, and its broader implications within mathematics and beyond. We'll explore the solution, analyze its geometric interpretation, and discuss its relevance in various fields.
Calculating 5 Squared Plus 12 Squared
The core of our exploration lies in the straightforward calculation:
- 5 squared (5²) = 5 x 5 = 25
- 12 squared (12²) = 12 x 12 = 144
Therefore, 5² + 12² = 25 + 144 = 169
This seemingly simple result, 169, holds significant mathematical weight, as we shall see.
The Pythagorean Theorem: A Geometric Interpretation
The true beauty of 5² + 12² = 169 reveals itself when we consider the Pythagorean theorem. This fundamental theorem of geometry states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). Formally:
a² + b² = c², where a and b are the lengths of the legs, and c is the length of the hypotenuse.
Our expression, 5² + 12² = 169, perfectly fits this mold. We can visualize a right-angled triangle with legs of length 5 and 12. The Pythagorean theorem tells us that the square of the hypotenuse (c²) is equal to 169. To find the length of the hypotenuse, we simply take the square root:
√169 = 13
Thus, a right-angled triangle with legs of length 5 and 12 has a hypotenuse of length 13. This specific triangle (5-12-13) is a well-known example of a Pythagorean triple – a set of three integers that satisfy the Pythagorean theorem.
Pythagorean Triples and their Significance
Pythagorean triples are sets of three integers (a, b, c) that satisfy the equation a² + b² = c². The 5-12-13 triple is just one example; others include (3, 4, 5) and (8, 15, 17). These triples are important in various areas of mathematics, including:
- Number Theory: The study of Pythagorean triples contributes significantly to our understanding of Diophantine equations (equations where only integer solutions are sought).
- Geometry: They are fundamental to constructing right-angled triangles and understanding geometric relationships.
- Trigonometry: Pythagorean triples provide simple examples for demonstrating trigonometric identities and ratios.
- Computer Science: Algorithms related to finding Pythagorean triples have applications in cryptography and computational geometry.
Extending the Concept: Beyond the 5-12-13 Triangle
While the 5-12-13 triangle is a prime example, the principle extends far beyond this single case. Any set of numbers that satisfy the Pythagorean theorem can be visualized geometrically as a right-angled triangle. The equation a² + b² = c² represents a fundamental relationship between the lengths of the sides in these triangles.
Applications in Real-World Scenarios
The Pythagorean theorem, and therefore the concept inherent in 5² + 12², finds numerous applications in the real world:
- Construction and Engineering: Calculating distances, determining angles, and ensuring structural stability are all reliant on the Pythagorean theorem. For example, architects use it to ensure that walls meet at right angles, and civil engineers use it in surveying and road construction.
- Navigation: GPS systems use the theorem to calculate distances and locations.
- Cartography: Mapmakers use the theorem to calculate distances on maps, where distances are often represented as coordinates.
- Physics: The Pythagorean theorem is frequently used in calculating vectors and resolving forces in various physics problems.
Mathematical Generalizations and Extensions
The concept underlying 5² + 12² can be generalized and extended in several mathematical directions:
- Higher Dimensions: The Pythagorean theorem can be extended to higher dimensions. For example, in three dimensions, the distance between two points is given by the formula: √(x² + y² + z²).
- Complex Numbers: The Pythagorean theorem relates directly to the magnitude of complex numbers. The magnitude of a complex number z = a + bi is given by √(a² + b²).
- Abstract Algebra: Concepts related to the Pythagorean theorem appear in various areas of abstract algebra, often in connection with inner product spaces and quadratic forms.
Further Explorations: Beyond the Basics
The seemingly simple calculation of 5² + 12² opens up avenues for more advanced mathematical exploration:
- Exploring other Pythagorean triples: Investigating methods for generating Pythagorean triples and exploring their properties is a rich mathematical pursuit.
- Fermat's Last Theorem: This famous theorem, proven by Andrew Wiles in 1994, is a generalization of the Pythagorean theorem. It states that there are no integer solutions to the equation aⁿ + bⁿ = cⁿ for any integer value of n greater than 2.
- Euclidean Geometry vs. Non-Euclidean Geometry: The Pythagorean theorem is a cornerstone of Euclidean geometry. Exploring non-Euclidean geometries, where the Pythagorean theorem does not hold, offers a deeper understanding of mathematical systems.
Frequently Asked Questions (FAQ)
Q: Are there infinitely many Pythagorean triples?
A: Yes, there are infinitely many Pythagorean triples. There are several formulas that can generate them.
Q: Is the 5-12-13 triangle the only triangle with integer sides?
A: No, it's one of many. Others include 3-4-5, 8-15-17, etc.
Q: What is the significance of the number 169 in this context?
A: 169 represents the square of the hypotenuse in a right-angled triangle with legs of length 5 and 12. It's also 13 squared.
Conclusion
The seemingly simple expression "5 squared plus 12 squared" serves as a gateway to a vast and fascinating world of mathematics. From the fundamental Pythagorean theorem to its applications in diverse fields and its connections to more advanced mathematical concepts, this seemingly straightforward calculation reveals the interconnectedness and beauty of mathematical principles. It encourages us to appreciate the power of seemingly simple mathematical operations and their profound implications in our understanding of the world around us. The exploration of 5² + 12² = 169 is not merely an exercise in calculation; it is a journey into the heart of mathematics itself.
Latest Posts
Latest Posts
-
Gcf Of 54 And 90
Sep 17, 2025
-
Lcm For 12 And 9
Sep 17, 2025
-
30 Days From May 20
Sep 17, 2025
-
4 6 As A Percentage
Sep 17, 2025
-
2 1 2 1 3
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5 Squared Plus 12 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.