500 Times What Equals 35
saludintensiva
Sep 21, 2025 · 5 min read
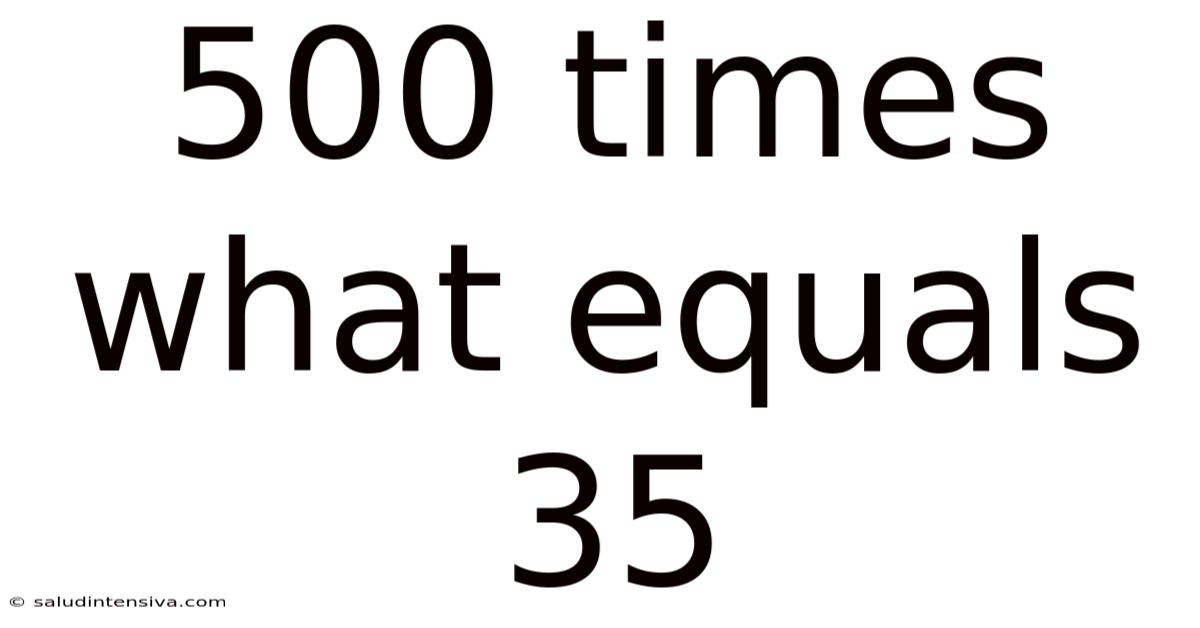
Table of Contents
Unveiling the Mystery: 500 Times What Equals 35? A Deep Dive into Proportion and Problem Solving
Finding the solution to "500 times what equals 35" might seem straightforward at first glance. However, delving deeper into this seemingly simple equation reveals a wealth of mathematical concepts, problem-solving strategies, and real-world applications. This article will not only provide the answer but also explore the underlying principles, offering a comprehensive understanding for learners of all levels. We'll journey from basic arithmetic to more advanced concepts, making this mathematical puzzle a stepping stone to broader mathematical literacy.
Understanding the Problem: Deconstructing the Equation
The core of the problem lies in understanding the phrase "500 times what." This translates mathematically into an algebraic equation:
500 * x = 35
Where 'x' represents the unknown quantity we are trying to find. The equation expresses a proportional relationship: 500 is to x as 35 is to 1. This means that if we scale 500 down to 1, we need to scale 35 down proportionally to find the value of x.
Solving the Equation: Step-by-Step Approach
Solving for 'x' involves isolating it on one side of the equation. This is achieved using inverse operations. Since 'x' is multiplied by 500, we perform the inverse operation – division – to find its value:
x = 35 / 500
Performing this division yields the answer:
x = 0.07
Therefore, 500 times 0.07 equals 35.
Beyond the Answer: Exploring Proportional Reasoning
The solution to this equation goes beyond a simple numerical answer. It highlights the fundamental concept of proportional reasoning, a cornerstone of mathematics and its applications in various fields. Proportional reasoning involves understanding relationships between quantities and how changes in one quantity affect another. This skill is crucial for:
- Scaling and resizing: Imagine enlarging a photograph. Understanding proportions ensures the image maintains its aspect ratio.
- Recipe adjustments: If a recipe calls for certain ingredients, understanding proportions allows you to scale the recipe up or down based on the number of servings.
- Map interpretation: Maps utilize scales to represent distances. Understanding proportions allows us to translate map distances to real-world distances.
- Financial calculations: Interest rates, discounts, and tax calculations all involve proportional relationships.
- Scientific experiments: Many scientific experiments involve manipulating variables and observing proportional changes in the results.
Different Approaches to Solving the Problem
While the method above is the most straightforward, there are other approaches to solving "500 times what equals 35":
- Using fractions: We can express the equation as a fraction: 35/500. Simplifying this fraction gives us 7/100, which is equivalent to 0.07.
- Using decimals: We can convert the fraction 35/500 to a decimal by performing the division.
- Using a calculator: A calculator provides the quickest way to find the answer by directly inputting 35 ÷ 500.
Each approach demonstrates different aspects of mathematical understanding, highlighting the interconnectedness of various mathematical concepts.
Real-World Applications and Examples
The concept of finding a number when you know the result of multiplying it by another number has numerous applications in daily life and across various professions. Let's explore a few examples:
- Business and Finance: A business might need to determine the unit cost of a product if they know the total cost and the number of units sold. This is directly analogous to our problem.
- Engineering: Engineers frequently encounter problems where they need to scale dimensions or calculate proportions in designs and constructions.
- Chemistry: Stoichiometry, a crucial part of chemistry, involves calculating the amounts of reactants and products in chemical reactions, relying heavily on proportional reasoning.
- Cooking: Scaling recipes up or down based on the number of servings requires a clear understanding of proportions.
Expanding Mathematical Understanding: Beyond Basic Arithmetic
The seemingly simple problem "500 times what equals 35" serves as a gateway to more advanced mathematical concepts:
- Algebra: The equation itself is an algebraic equation, introducing the use of variables and solving for unknowns. This forms the basis of algebraic manipulation and solving more complex equations.
- Calculus: Calculus deals with rates of change and functions, which build upon a strong foundation in proportional reasoning and algebraic manipulation.
- Statistics: Many statistical calculations involve proportions and ratios, making a solid understanding of proportional reasoning essential.
Addressing Potential Challenges and Misconceptions
Students may encounter some challenges when solving problems like this. Common misconceptions include:
- Incorrect order of operations: Students might incorrectly perform the division before the multiplication.
- Difficulty with decimal numbers: Working with decimal numbers can be challenging for some students.
- Lack of understanding of proportional relationships: A solid grasp of proportions is vital to solving these types of problems correctly.
To overcome these challenges, a step-by-step approach, visual aids, and plenty of practice are key.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this problem using a different method? A: Yes, as mentioned earlier, there are multiple approaches, including using fractions, decimals, or a calculator. The best method depends on your comfort level and available tools.
-
Q: What if the numbers were larger or smaller? A: The process remains the same. You would still divide the given result by the known multiplier to find the unknown factor.
-
Q: Are there similar problems I can practice with? A: Yes, try problems like "25 times what equals 100," or "10 times what equals 3." These will reinforce your understanding of proportional reasoning.
-
Q: What if the equation was written differently? A: The underlying principle remains the same, even if the equation is written differently (e.g., "What number multiplied by 500 equals 35?"). Focus on identifying the unknown and using inverse operations to solve.
Conclusion: Mastering Proportions and Problem-Solving
Solving "500 times what equals 35" is more than just finding the answer (0.07). It’s about understanding the underlying principles of proportional reasoning and applying these principles to various mathematical contexts. This seemingly simple equation serves as a microcosm of mathematical problem-solving, highlighting the importance of understanding concepts, applying appropriate methods, and verifying results. By mastering these skills, you're not only solving a mathematical problem but also building a stronger foundation for future mathematical endeavors. The journey from a simple equation to a broader understanding of proportion and problem-solving showcases the power of mathematical thinking and its relevance to numerous aspects of life. Continue practicing and exploring different mathematical concepts to further enhance your mathematical literacy.
Latest Posts
Latest Posts
-
How Long Is 79 Minutes
Sep 21, 2025
-
10 By 10 Coordinate Grid
Sep 21, 2025
-
Kg Meter Per Second Squared
Sep 21, 2025
-
30 Days Before June 30
Sep 21, 2025
-
60 Days From December 2nd
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 500 Times What Equals 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.