6 1/2 As A Decimal
saludintensiva
Sep 16, 2025 · 5 min read
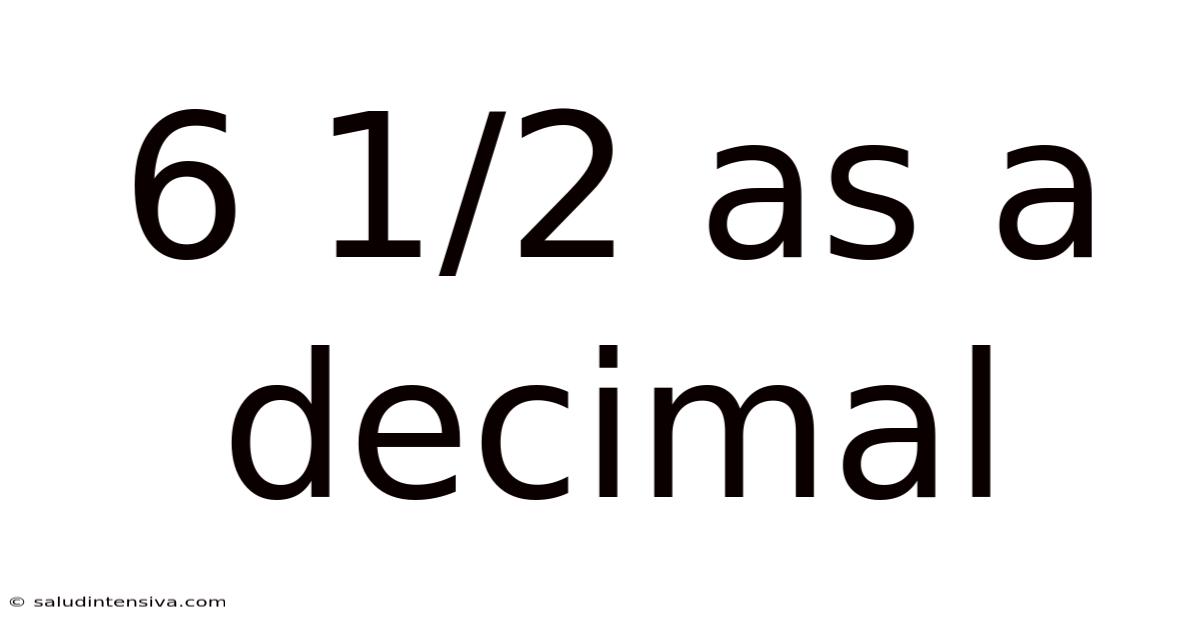
Table of Contents
Understanding 6 1/2 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 6 1/2 into its decimal equivalent, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll cover multiple methods, address common misconceptions, and explore the broader context of decimal representation.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's refresh our understanding of the terms involved. A mixed number combines a whole number and a fraction, like 6 1/2. A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. For example, 6.5 is a decimal. The process of converting a mixed number to a decimal involves expressing the fractional part as a decimal and then combining it with the whole number.
Method 1: Converting the Fraction to a Decimal
This is the most straightforward method. We first focus on converting the fractional part (1/2) into its decimal equivalent. To do this, we perform a simple division:
1 ÷ 2 = 0.5
Therefore, 1/2 is equal to 0.5. Now, we simply add the whole number part (6) to get the final decimal:
6 + 0.5 = 6.5
So, 6 1/2 as a decimal is 6.5.
Method 2: Converting to an Improper Fraction
An alternative approach involves first converting the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. To convert 6 1/2 to an improper fraction:
- Multiply the whole number by the denominator: 6 x 2 = 12
- Add the numerator to the result: 12 + 1 = 13
- Keep the same denominator: 13/2
Now, we divide the numerator by the denominator:
13 ÷ 2 = 6.5
Again, we arrive at the same decimal equivalent: 6.5.
Method 3: Understanding Place Value
Understanding place value provides a deeper insight into the conversion process. The decimal system is based on powers of 10. Each position to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
In 6 1/2, the fraction 1/2 represents one-half, or 0.5, which corresponds to the tenths place. Therefore, 6 1/2 can be directly written as 6.5.
Visual Representation: The Number Line
A number line provides a visual aid to grasp the relationship between fractions and decimals. Locate 6 on the number line. Then, divide the space between 6 and 7 into ten equal parts. Each part represents one-tenth (0.1). The point halfway between 6 and 7 will represent 6.5, which is equivalent to 6 1/2.
Practical Applications of Decimal Conversion
Converting fractions to decimals is essential in numerous real-world scenarios:
- Financial calculations: Dealing with money involves decimal representation (dollars and cents). Converting fractions of dollars into decimals is crucial for accurate calculations. For example, $6 1/2 is equivalent to $6.50.
- Measurements: Many measurement systems utilize decimals. For instance, if a recipe calls for 6 1/2 cups of flour, you would likely use a measuring cup to measure 6.5 cups.
- Scientific calculations: Scientific computations often involve decimal representation for precise measurements and calculations.
- Data analysis: In statistical analysis and data representation, decimals are commonly used for expressing proportions, percentages, and averages.
- Computer programming: Decimals are the foundation of numerical representation in most programming languages.
Common Misconceptions and Troubleshooting
- Confusing the numerator and denominator: Ensure you correctly divide the numerator by the denominator when converting the fraction to a decimal.
- Incorrect decimal placement: Pay close attention to the position of the decimal point. A misplaced decimal point can significantly alter the value.
- Rounding errors: When dealing with repeating decimals, you may need to round the decimal to a specific number of decimal places, depending on the context.
Expanding on Decimal Representation: Repeating Decimals
While 6 1/2 conveniently converts to a terminating decimal (6.5), not all fractions result in terminating decimals. Some fractions produce repeating decimals. For example, 1/3 equals 0.3333... (the 3 repeats infinitely). Understanding repeating decimals is crucial for more advanced mathematical applications. Representing repeating decimals can be done using a bar notation (e.g., 0.3̅) to indicate the repeating digit(s).
Exploring Further: Converting Other Mixed Numbers to Decimals
Let's extend our understanding by converting a few more mixed numbers to decimals using the methods described above:
- 7 3/4: 3/4 = 0.75, so 7 3/4 = 7.75
- 2 1/5: 1/5 = 0.2, so 2 1/5 = 2.2
- 10 2/3: 2/3 = 0.666... (repeating decimal), so 10 2/3 ≈ 10.67 (rounded to two decimal places)
Frequently Asked Questions (FAQ)
Q1: Can all fractions be expressed as decimals?
A1: Yes, all fractions can be expressed as decimals. However, some will be terminating decimals (ending after a finite number of digits), while others will be repeating decimals (having a digit or group of digits that repeat infinitely).
Q2: How do I convert a decimal back to a fraction?
A2: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (10, 100, 1000, etc.), depending on the number of digits after the decimal point. Then, simplify the fraction to its lowest terms. For example, 0.75 = 75/100 = 3/4.
Q3: Why is understanding decimal representation important?
A3: Decimal representation is fundamental for performing calculations, making measurements, analyzing data, and understanding various concepts across multiple fields, including finance, science, and technology.
Conclusion: Mastering Decimal Conversions
Converting fractions to decimals, and vice-versa, is a core mathematical skill with far-reaching applications. Understanding the different methods, particularly the process of converting fractions to decimals, is essential for anyone working with numbers. Whether you're balancing your budget, following a recipe, or conducting scientific research, a solid grasp of decimal representation is invaluable. Through practice and a firm understanding of the underlying principles, you can confidently navigate the world of numbers and unlock their full potential. Remember, the key is to break down the problem into manageable steps and to utilize the various techniques discussed to ensure accuracy and efficiency.
Latest Posts
Latest Posts
-
39 40 As A Decimal
Sep 16, 2025
-
3 To The 1 2 Power
Sep 16, 2025
-
17 24 As A Percentage
Sep 16, 2025
-
What Is 4 Of 85000
Sep 16, 2025
-
How To Calculate Percentage Excel
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 6 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.